DeepXDE: 一个强大的科学机器学习和物理信息学习库

DeepXDE简介

DeepXDE是一个强大的开源深度学习库,专门用于解决微分方程和物理信息学习问题。它由Lu Lu在布朗大学George Karniadakis教授的指导下开发,目前由耶鲁大学维护。DeepXDE集成了多种先进的算法和技术,为科学计算和工程应用提供了一个灵活而强大的工具。

DeepXDE的核心是物理信息神经网络(Physics-Informed Neural Networks, PINNs)算法。这种方法将物理定律作为约束条件嵌入到神经网络的损失函数中,从而能够在保证物理一致性的同时学习复杂系统的行为。除了PINNs,DeepXDE还包含了其他重要算法,如深度算子网络(DeepONet)和多保真度神经网络(MFNN)等。

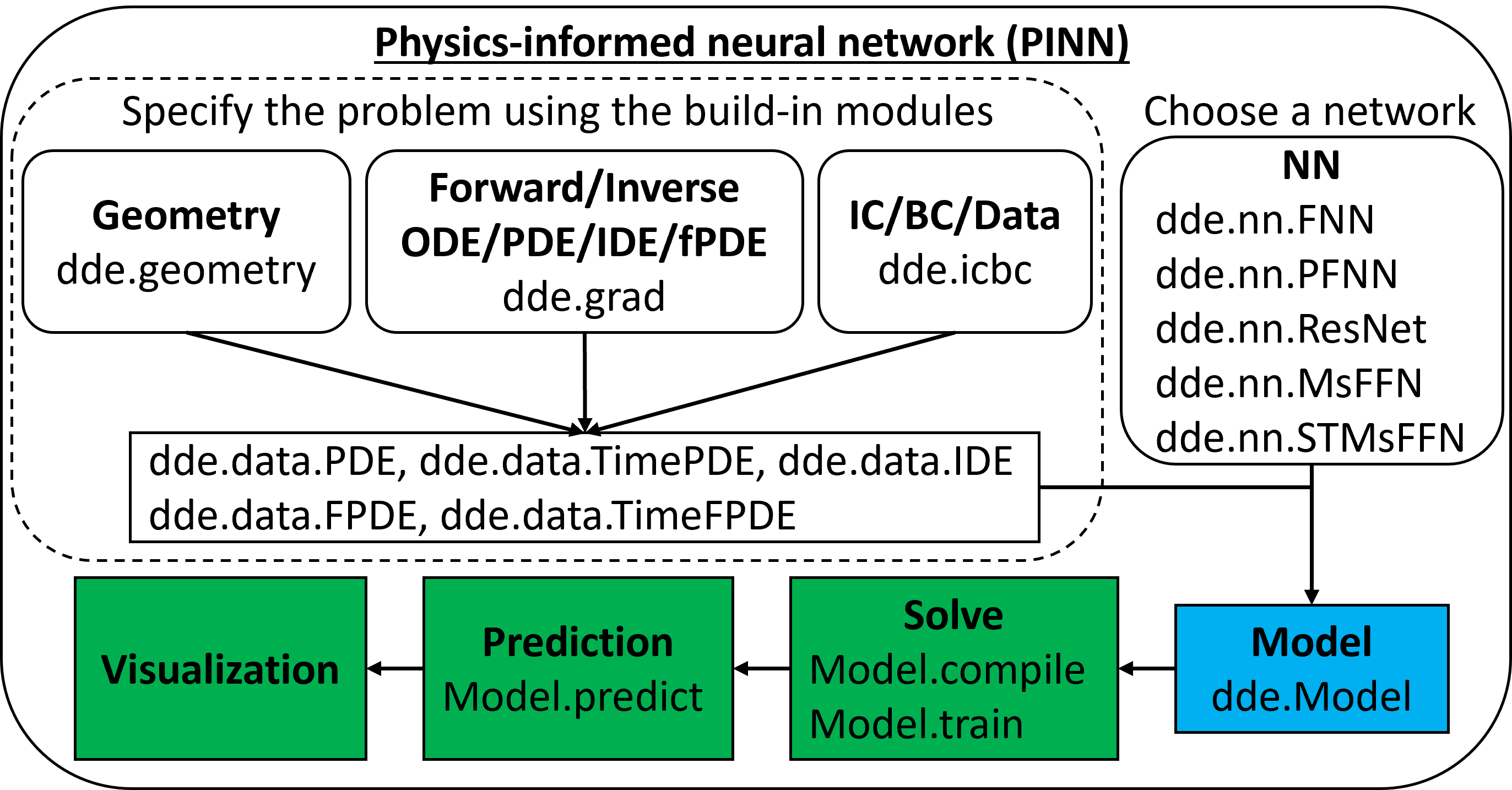
PINN算法示意图

DeepXDE的主要特性

DeepXDE具有以下突出特点:

多样化的问题求解能力:
- 求解正/逆常微分方程(ODEs)和偏微分方程(PDEs)
- 求解积分-微分方程(IDEs)
- 求解分数阶PDEs(fPDEs)
- 求解随机PDEs(sPDEs)
- 求解逆设计/拓扑优化问题
先进的精度提升技术:
- 基于残差的自适应采样
- 梯度增强PINN(gPINN)
- 多尺度傅里叶特征PINN
复杂几何处理能力:
- 支持多种基本几何形状:区间、三角形、矩形、多边形、圆盘、椭圆、星形、长方体、球体、超立方体、超球面等
- 通过布尔运算(并集、差集、交集)构造复杂几何
- 支持点云表示的几何
多种边界条件:
- Dirichlet边界条件
- Neumann边界条件
- Robin边界条件
- 周期性边界条件
- 一般边界条件
灵活的神经网络架构:
- 全连接神经网络(FNN)
- 堆叠FNN
- 残差神经网络
- 时空多尺度傅里叶特征网络等
多种采样方法:
- 均匀采样
- 伪随机采样
- 拉丁超立方采样
- Halton序列
- Hammersley序列
- Sobol序列
丰富的优化器选择:
- Adam优化器
- L-BFGS优化器等
多GPU并行训练支持
不确定性量化:
- 使用dropout进行不确定性量化
多精度支持:
- float16
- float32
- float64
多种后端支持:
- TensorFlow 1.x和2.x
- PyTorch
- JAX
- PaddlePaddle

DeepXDE的这些特性使其能够应对各种复杂的科学计算和工程问题,为研究人员和工程师提供了一个强大而灵活的工具。

DeepXDE的应用场景

DeepXDE可以应用于多个领域的问题求解:

偏微分方程求解: DeepXDE可以高效地求解各种类型的偏微分方程,包括椭圆型、抛物型和双曲型方程。这在流体力学、热传导、量子力学等领域有广泛应用。
逆问题求解: 通过利用有限的观测数据,DeepXDE能够推断出系统的参数或初始条件。这在地球物理、医学成像等领域特别有用。
多物理场耦合问题: DeepXDE支持多物理场耦合问题的求解,如流固耦合、热-机耦合等复杂系统。
算子学习: 通过DeepONet算法,DeepXDE可以学习复杂的非线性算子,这在降阶模型、控制系统设计等方面有重要应用。
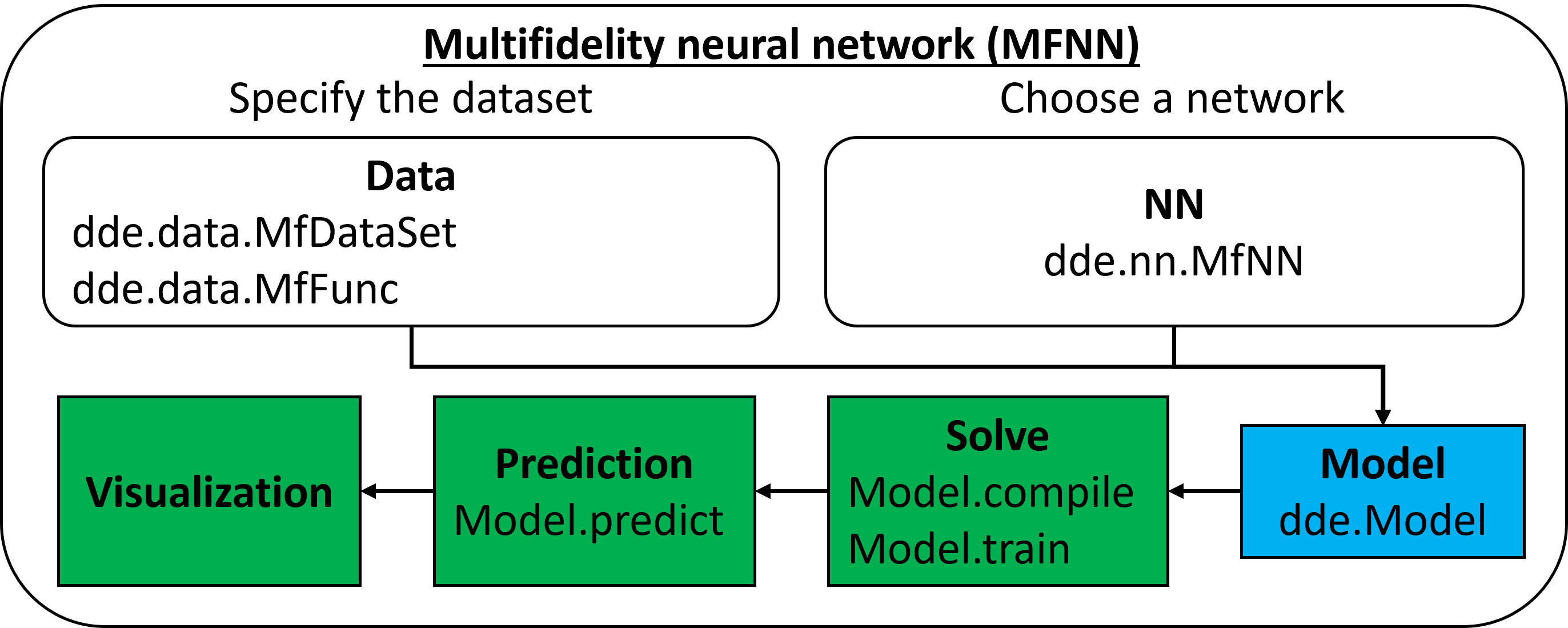
多保真度数据学习: 利用MFNN算法,DeepXDE能够有效地整合不同精度级别的数据,这在多尺度模拟、实验设计等领域非常有用。
不确定性量化: DeepXDE提供了使用dropout进行不确定性量化的功能,这在风险评估、可靠性分析等方面有重要应用。

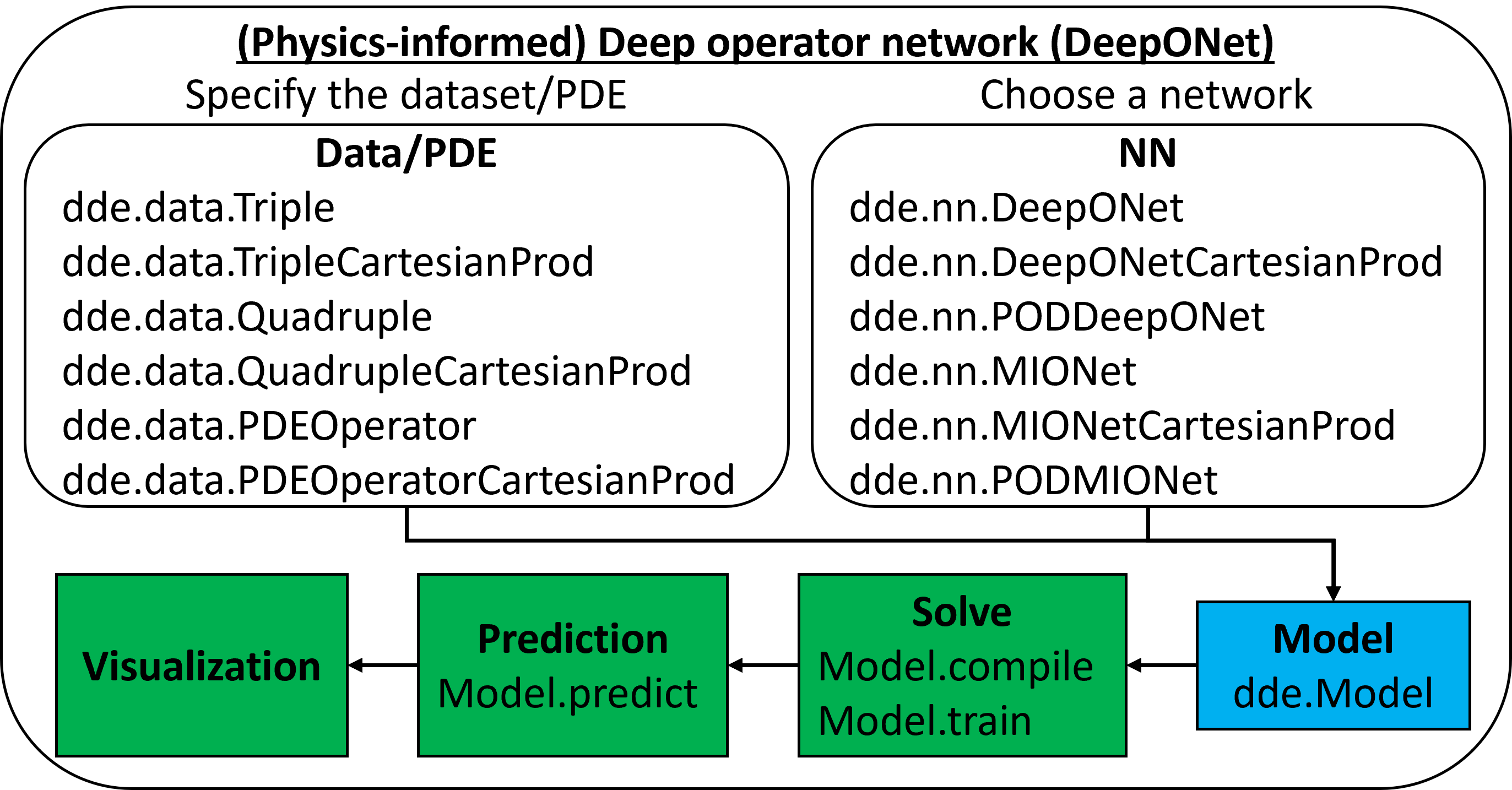
DeepONet算法示意图

DeepXDE的安装和使用

DeepXDE的安装非常简单,可以通过pip或conda进行安装:

pip install deepxde

或

conda install -c conda-forge deepxde

DeepXDE支持多种后端,用户可以根据自己的需求选择合适的后端:

TensorFlow 1.x或2.x
PyTorch
JAX
PaddlePaddle

使用DeepXDE解决问题通常遵循以下步骤:

定义问题的几何和边界条件
设置PDE或其他方程
创建神经网络模型
编译模型
训练模型
预测和后处理结果

下面是一个简单的例子,展示如何使用DeepXDE求解一维Poisson方程:

import deepxde as dde
import numpy as np

def pde(x, y):
    dy_xx = dde.grad.hessian(y, x)
    return -dy_xx - np.pi**2 * dde.sin(np.pi * x)

def boundary(x, on_boundary):
    return on_boundary

geom = dde.geometry.Interval(0, 1)
bc = dde.icbc.DirichletBC(geom, lambda x: 0, boundary)
data = dde.data.PDE(geom, pde, bc, 16, 2, solution=lambda x: np.sin(np.pi * x), num_test=100)

layer_size = [1] + [50] * 3 + [1]
activation = "tanh"
initializer = "Glorot uniform"
net = dde.nn.FNN(layer_size, activation, initializer)

model = dde.Model(data, net)
model.compile("adam", lr=0.001, metrics=["l2 relative error"])
losshistory, train_state = model.train(epochs=10000)

dde.saveplot(losshistory, train_state, issave=True, isplot=True)

这个例子展示了DeepXDE的基本用法,包括定义PDE、设置边界条件、创建神经网络模型、编译和训练模型等步骤。

DeepXDE的未来发展

作为一个活跃的开源项目,DeepXDE正在不断发展和改进。未来的发展方向可能包括:

更多算法的集成: 集成更多先进的科学机器学习算法,如物理信息图神经网络(PI-GNN)等。
性能优化: 进一步提高大规模问题的计算效率,可能通过更高效的并行计算策略或利用专门的硬件加速器。
更广泛的应用支持: 扩展到更多的科学和工程领域,如量子计算、材料科学等。
自动化和智能化: 开发更智能的自动调参和模型选择功能,减少用户的手动干预。
与其他工具的集成: 加强与传统数值方法工具的集成,实现混合求解策略。
可解释性增强: 提供更多的工具来解释和可视化神经网络的决策过程。

多保真度神经网络示意图

结论

DeepXDE作为一个强大的科学机器学习和物理信息学习库,为科研人员和工程师提供了一个灵活而高效的工具,用于解决各种复杂的微分方程和物理问题。它的多功能性、易用性和可扩展性使其在科学计算和工程应用领域具有广阔的前景。随着持续的开发和社区贡献,DeepXDE有望在推动科学机器学习领域的发展中发挥更大的作用。

对于那些需要处理复杂物理系统、多尺度问题或大规模数据的研究人员和工程师来说,DeepXDE无疑是一个值得关注和尝试的工具。它不仅能够帮助解决传统方法难以处理的问题,还能为科学发现和工程创新提供新的思路和方法。

如果您对DeepXDE感兴趣,可以访问其GitHub仓库了解更多信息,或查阅其官方文档获取详细的使用指南。同时,DeepXDE的开发团队也欢迎社区贡献,无论是报告问题、提出改进建议,还是直接参与代码开发,都能够帮助这个项目变得更好。让我们共同期待DeepXDE在科学机器学习领域创造更多的可能性!