DiffEqFlux.jl: 融合微分方程与机器学习的Julia库

DiffEqFlux.jl:融合微分方程与机器学习的Julia库

DiffEqFlux.jl是一个强大的Julia库,旨在将微分方程的世界与机器学习融合。该库通过帮助用户将微分方程求解器嵌入神经网络中,为科学机器学习和物理信息机器学习研究提供了强大的工具。

库的核心功能与特点

DiffEqFlux.jl的核心在于它能够将微分方程求解器无缝集成到神经网络架构中。这种融合为研究人员和工程师提供了一种独特的方法,可以在传统机器学习模型中注入物理知识和动力学信息。该库利用了Julia生态系统中两个强大的组件:DifferentialEquations.jl和Lux.jl,作为其构建基础。

DifferentialEquations.jl是Julia中最全面的微分方程求解器库之一,提供了广泛的数值方法来处理各种类型的微分方程。另一方面,Lux.jl是一个灵活的深度学习框架,专为科学计算和高性能应用而设计。通过结合这两个库的优势,DiffEqFlux.jl创建了一个独特的平台,特别适合科学机器学习应用。

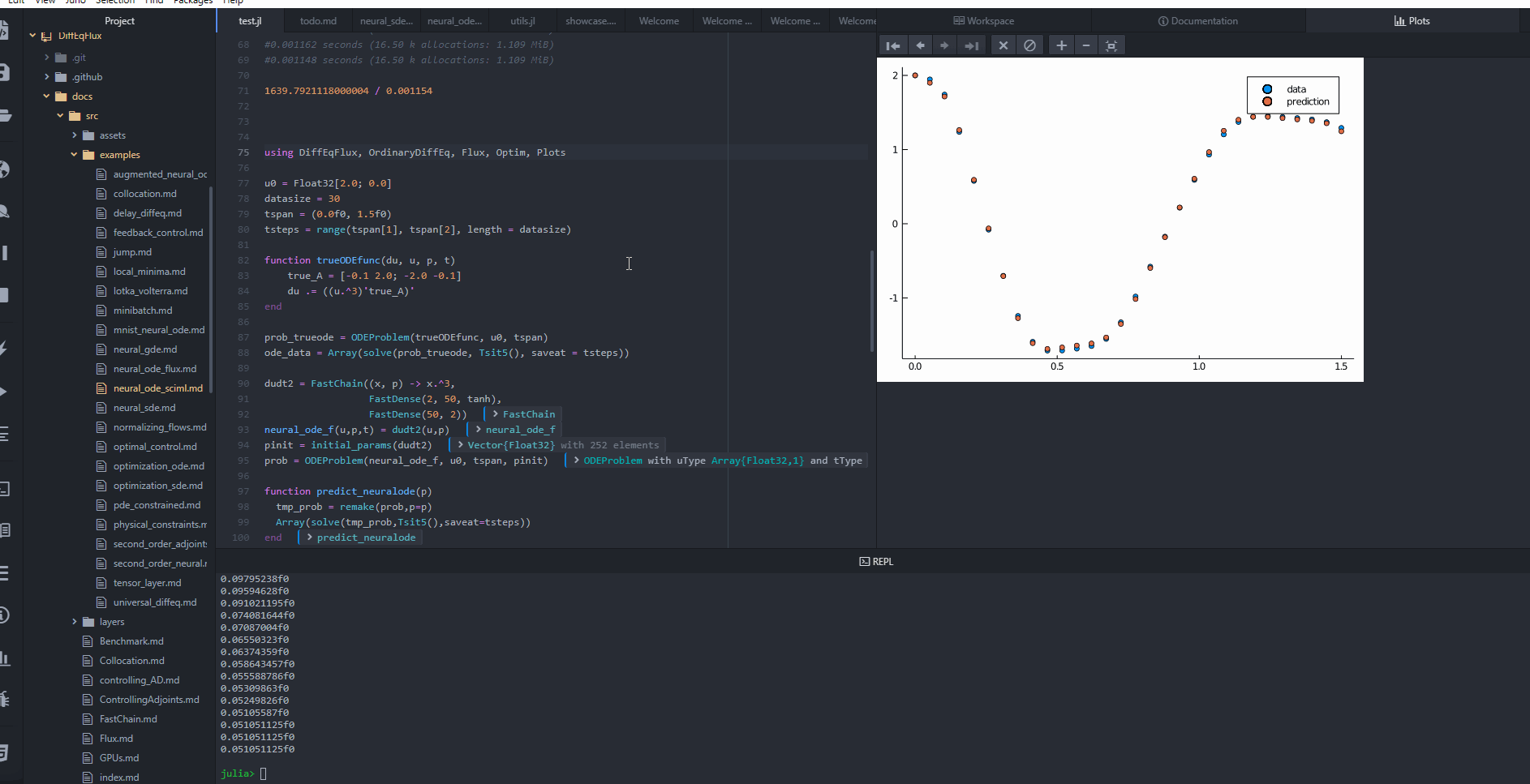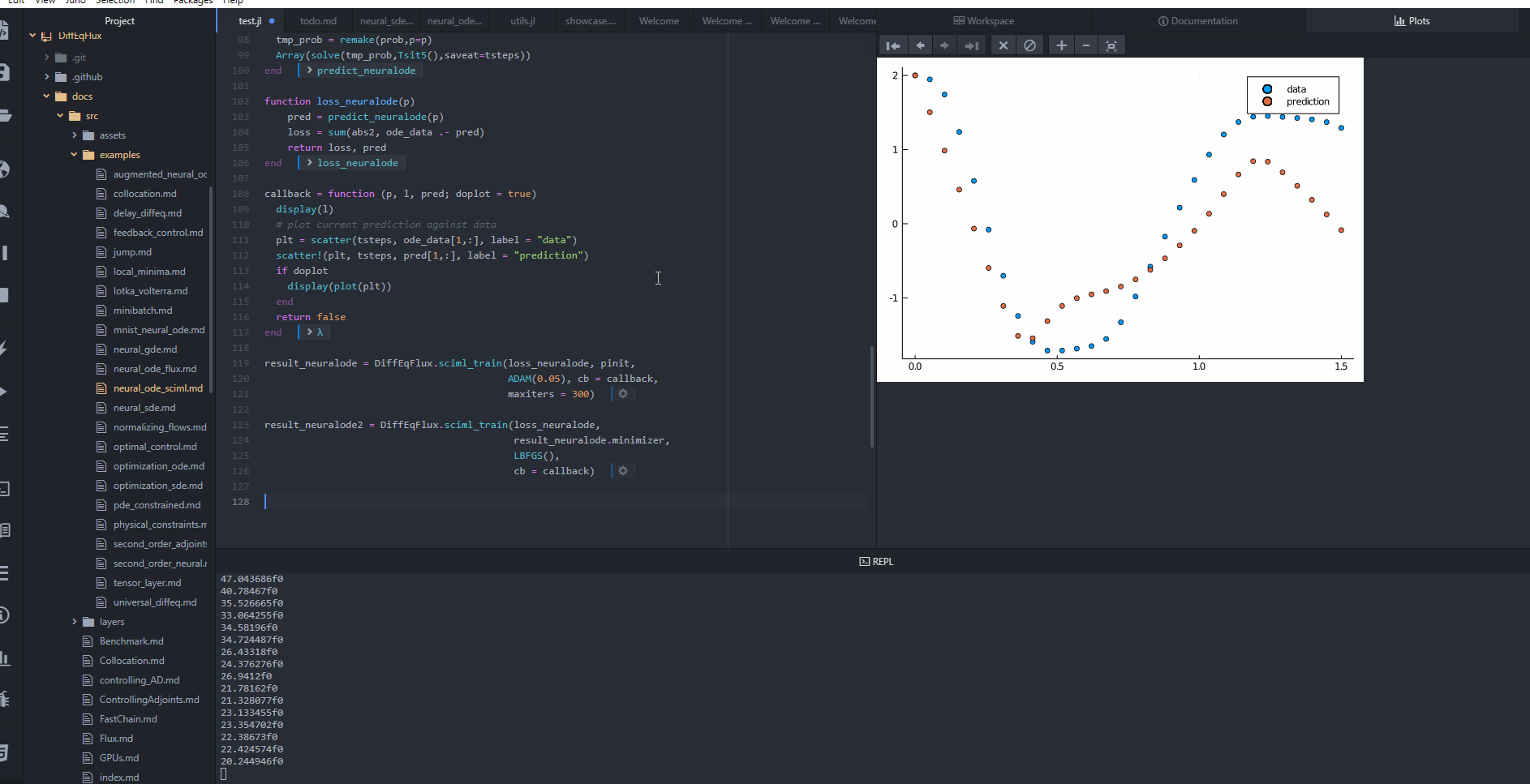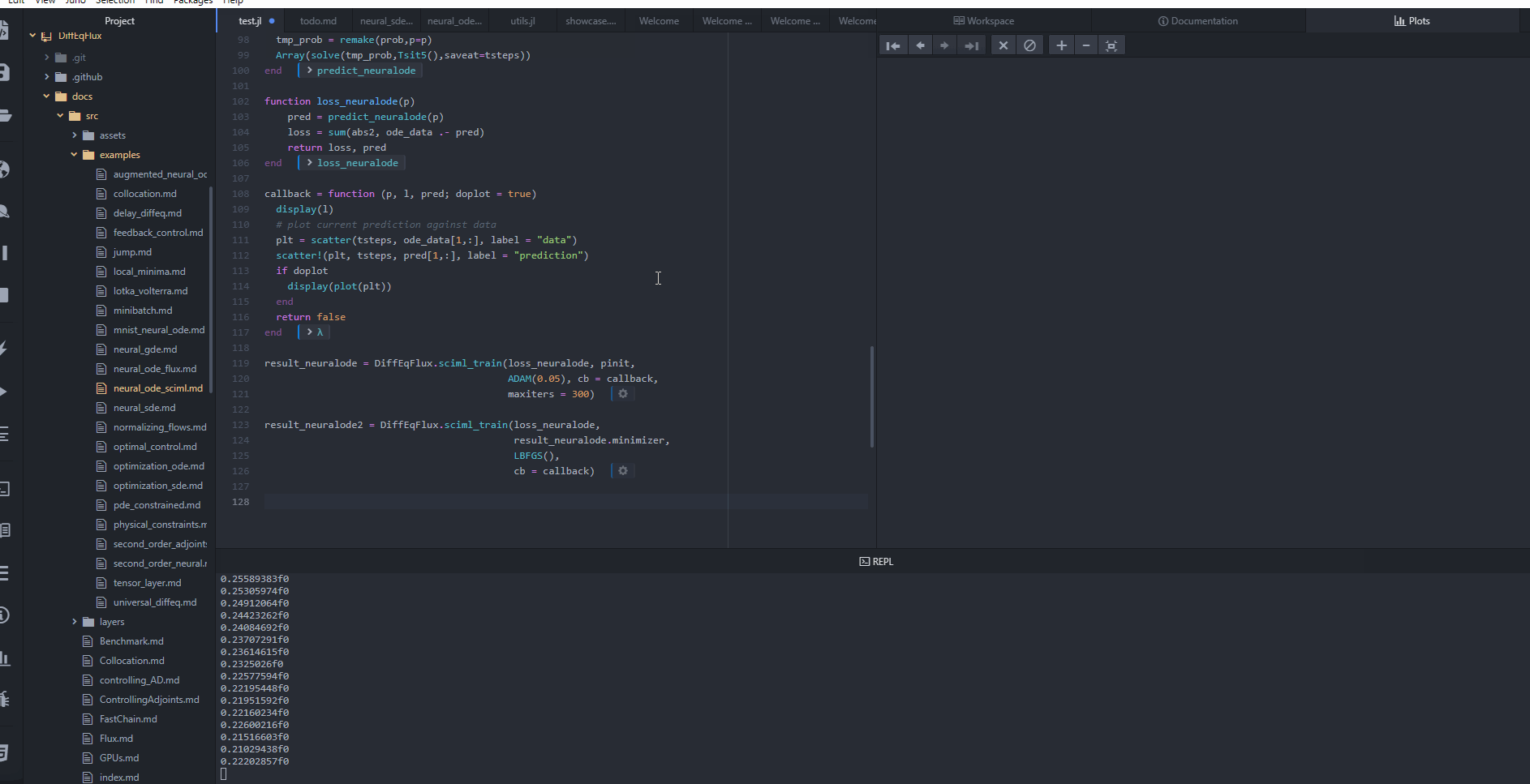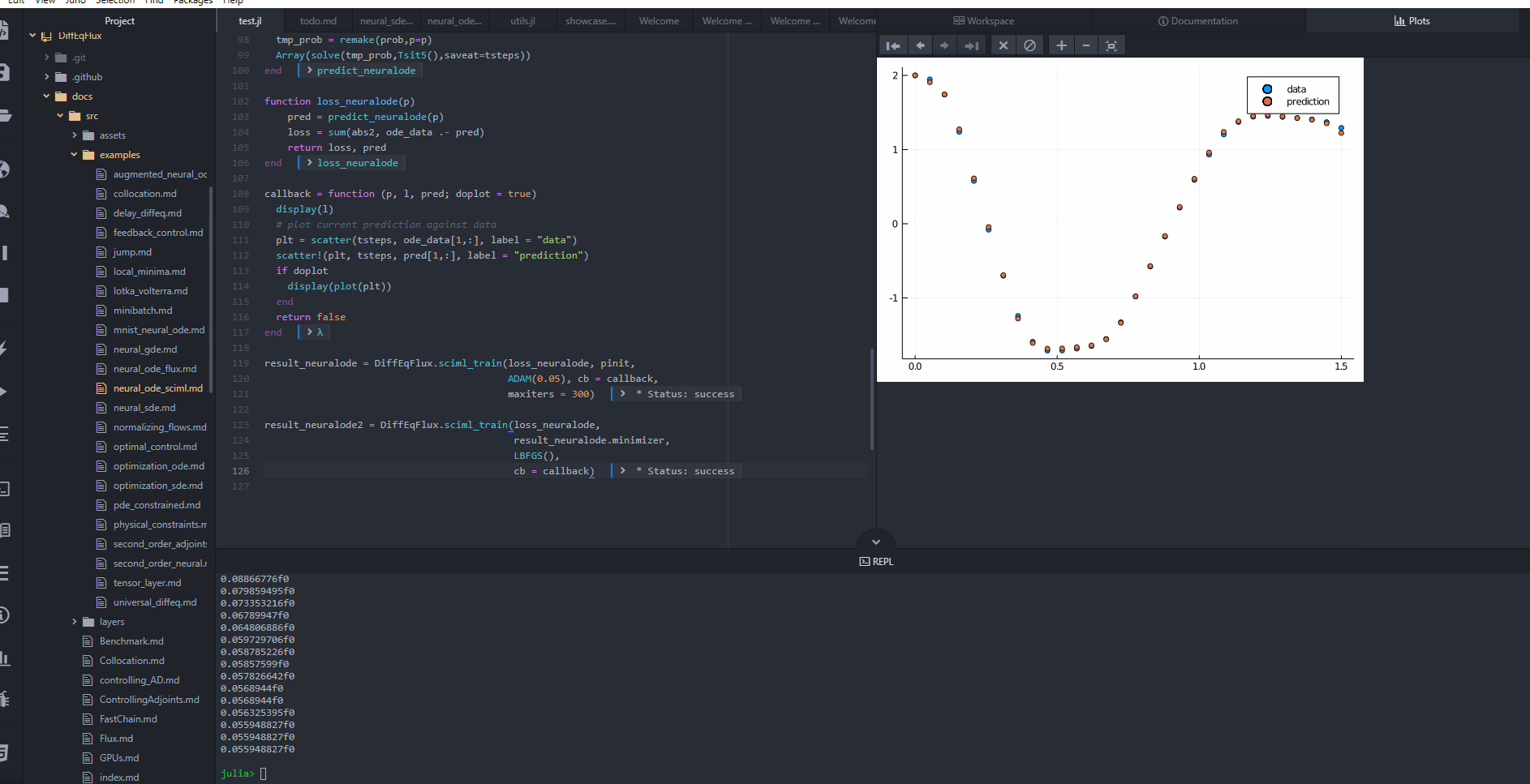
DiffEqFlux.jl架构

主要应用领域

DiffEqFlux.jl主要面向隐式层机器学习领域。它提供了一系列架构,这些架构与Flux.jl和Lux.jl等机器学习库的接口相匹配,使得将连续时间机器学习层集成到更大的机器学习应用中变得简单直观。这种设计理念使得DiffEqFlux.jl特别适合于以下应用:

科学机器学习(SciML): 该库为研究人员提供了工具,以开发能够利用科学知识和物理规律的机器学习模型。这对于提高模型在科学和工程领域的准确性和可解释性至关重要。
物理信息机器学习: 通过允许将物理方程直接编码到神经网络架构中,DiffEqFlux.jl支持开发能够遵守已知物理定律的模型。
神经微分方程: 该库支持多种类型的神经微分方程,包括神经常微分方程(Neural ODEs)、神经随机微分方程(Neural SDEs)等,为时间序列建模和动态系统分析提供了强大的工具。

支持的神经微分方程类型

DiffEqFlux.jl支持广泛的神经微分方程类型,为研究人员提供了丰富的工具集来建模复杂系统:

神经常微分方程(Neural ODEs): 这是最基本的形式,允许将神经网络嵌入到常微分方程中。
基于配点的神经ODEs: 这种方法不使用求解器,是目前最快的实现方式。
多重射击神经常微分方程: 这种技术可以提高长时间序列的稳定性和精度。
神经随机微分方程(Neural SDEs): 用于建模具有随机性的系统。
神经代数微分方程(Neural DAEs): 适用于受代数约束的系统。
神经延迟微分方程(Neural DDEs): 用于建模具有时间延迟的系统。
增广神经ODEs: 这种方法通过增加状态空间的维度来提高模型的表达能力。
哈密顿神经网络: 专门用于建模保守系统,配有专门的二阶和辛积分器。
连续正则化流(CNF)和FFJORD: 这些是用于生成模型和概率流的特殊架构。

这些方法都配备了高阶、自适应、隐式、GPU加速、Newton-Krylov等先进的数值技术,使得DiffEqFlux.jl能够处理各种复杂的科学计算问题。

性能与灵活性

DiffEqFlux.jl的一个关键优势是其性能。该库实现了O(1)反向传播,这意味着梯度计算的时间复杂度不随网络深度的增加而增加。这一特性使得DiffEqFlux.jl特别适合于深度神经微分方程模型的训练。

此外,该库还提供了GPU加速支持,允许用户在图形处理单元上运行计算密集型模型,从而显著减少训练时间。对于处理刚性和非刚性微分方程的能力进一步扩展了库的应用范围,使其能够处理广泛的科学和工程问题。

使用示例与文档

为了帮助用户快速上手,DiffEqFlux.jl提供了全面的文档和丰富的示例。用户可以在稳定版文档中找到详细的使用说明和API参考。对于那些希望尝试最新功能的用户,还可以查阅开发版文档。

库的灵活性允许用户以多种方式探索微分方程与机器学习的结合:

可以定义神经网络,其中"激活函数"是由微分方程描述的非线性函数。
可以构建神经网络,其中某些层是ODE求解。
可以定义ODE,其中某些项是神经网络。
可以在ODE上定义代价函数来构建神经网络。

这种灵活性为研究人员提供了广阔的探索空间,使他们能够开发出创新的模型来解决复杂的科学和工程问题。

社区支持与发展

DiffEqFlux.jl拥有一个活跃的开发社区,不断推动库的功能和性能进步。该项目遵循ColPrac贡献者指南,鼓励社区成员参与到库的开发中来。此外,项目还采用了SciML代码风格,确保代码库的一致性和可维护性。

库的开发过程是透明的,用户可以在GitHub仓库上跟踪进展,提出问题,或贡献代码。这种开放的开发模式确保了DiffEqFlux.jl能够持续改进并适应科学机器学习领域的最新发展。

未来展望

随着科学机器学习领域的快速发展,DiffEqFlux.jl也在不断evolve to meet new challenges. 未来的发展方向可能包括:

进一步优化性能,特别是对于大规模系统和长时间序列。
扩展对更多类型微分方程的支持,如偏微分方程(PDEs)。
改进与其他机器学习框架的集成和互操作性。
开发更多针对特定科学领域的预构建模型和工具。

总的来说,DiffEqFlux.jl代表了科学计算和机器学习交叉领域的一个重要进展。通过提供一个强大、灵活且高效的平台来结合微分方程与神经网络,它为科学家和工程师提供了一个独特的工具,以开发能够捕捉复杂物理系统本质的智能模型。随着科学机器学习领域的不断发展,DiffEqFlux.jl无疑将继续在推动这一前沿领域的进步中发挥关键作用。