GFlowNet: 一种新型生成式模型框架及其在分子设计中的应用

GFlowNet简介

GFlowNet(Generative Flow Network)是由Yoshua Bengio等人于2021年提出的一种新型生成式模型框架。与传统的生成模型不同,GFlowNet特别适用于离散、组合对象的生成,如分子结构、图结构等。它通过学习在有向无环图中的流来实现对目标分布的采样,为解决复杂的组合优化问题提供了新的思路。

GFlowNet的核心思想是将对象的构建过程建模为有向无环图中的流。每个节点代表一个部分构建的对象,边代表构建动作。通过学习这个图中的流,GFlowNet可以生成与目标分布成比例的样本。这种方法不仅能产生多样化的高质量样本,还可以有效地探索未知的高奖励区域。

GFlowNet的工作原理

流网络建模

GFlowNet将对象的构建过程建模为一个有向无环图,称为流网络。在这个网络中:

• 每个节点代表一个部分构建的对象状态
• 边代表从一个状态到另一个状态的转移动作
• 源节点代表初始空状态
• 汇节点代表完全构建的对象

网络中的流量定义了从源节点到汇节点的概率分布。GFlowNet的目标是学习一个流函数,使得到达每个汇节点的流量与该节点对应对象的目标概率成正比。

流一致性方程

为了学习合适的流函数,GFlowNet引入了流一致性方程。对于非源节点s',流一致性方程要求:

∑(s,a:T(s,a)=s') F(s,a) = R(s') + ∑(a'∈A(s')) F(s',a')

其中F(s,a)表示从状态s经动作a的流量,R(s')表示s'的奖励(如果s'是汇节点),A(s')表示s'的可用动作集。

训练目标

GFlowNet的训练目标是最小化流一致性方程的违反程度。具体来说,损失函数定义为:

L(θ) = ∑(s'≠s0) (log[ϵ + ∑(s,a:T(s,a)=s') exp(Fθ(s,a))] - log[ϵ + R(s') + ∑(a'∈A(s')) exp(Fθ(s',a'))])^2

其中Fθ表示参数化的流函数,ϵ是一个小的正数用于数值稳定性。

GFlowNet在分子设计中的应用

GFlowNet在分子设计领域展现出了巨大的潜力。传统的分子设计方法通常难以在高维离散空间中有效探索,而GFlowNet提供了一种新的范式。

分子图生成

在分子设计任务中,GFlowNet将分子的构建过程建模为逐步添加原子和键的过程。具体来说:

1. 状态表示:每个状态表示一个部分构建的分子图。
2. 动作空间:包括添加新原子、添加新键、结束生成等动作。
3. 奖励函数:根据分子的目标属性(如结合亲和力、可溶性等)定义。

使用图神经网络(GNN)作为策略网络,GFlowNet可以学习到有效的分子构建策略。

多目标优化

GFlowNet天然适合处理多目标优化问题。通过定义多维奖励函数,GFlowNet可以同时优化分子的多个属性,如药效、毒性、合成难度等。这为药物发现提供了强大的工具。

活性学习

在实际应用中,精确的奖励函数通常难以获得。GFlowNet可以与活性学习结合,通过迭代采样和评估来逐步改进模型。这种方法可以大大减少昂贵实验的需求,提高分子设计的效率。

GFlowNet与其他方法的比较

与MCMC方法的比较

相比于马尔可夫链蒙特卡洛(MCMC)方法,GFlowNet具有以下优势:

1. 直接生成:无需长链采样,可快速生成样本。
2. 模式发现:能更有效地发现和跳转到远离当前分布的新模式。
3. 并行化:生成过程天然可并行,提高效率。

与强化学习的比较

与传统强化学习方法相比,GFlowNet的优势包括:

1. 多样性:通过拟合整个分布而非最大化期望奖励,能生成更多样的样本。
2. 探索效率:更容易发现和利用远离当前策略的高奖励区域。
3. 稳定性:训练过程更加稳定,不易陷入局部最优。

GFlowNet的实际应用案例

片段化分子设计

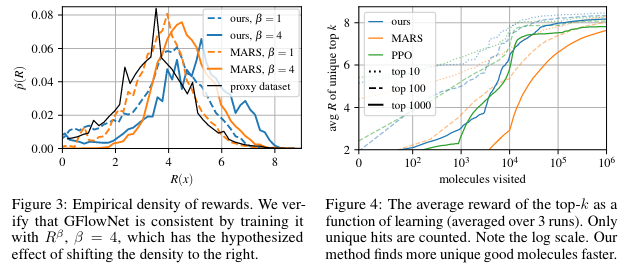
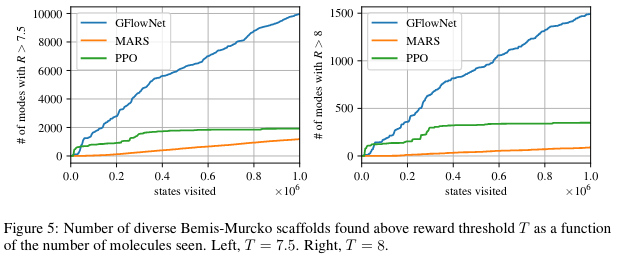
研究人员使用GFlowNet进行了基于片段的分子设计,目标是优化针对sEH蛋白的分子。结果表明,GFlowNet能够生成多样化的高质量候选分子,超越了传统的PPO和MARS方法。

多目标优化分子设计

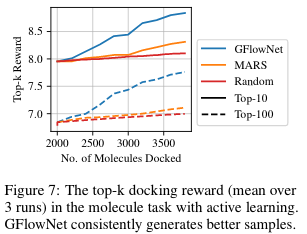
在另一项研究中,GFlowNet被应用于多目标优化分子设计任务,同时考虑了分子的QED、SA和分子量等多个目标。实验结果显示,GFlowNet能够有效地在多个目标之间进行权衡,生成满足复杂要求的分子。

GFlowNet的未来发展方向

尽管GFlowNet已经展现出了巨大的潜力,但它仍处于快速发展阶段。一些值得关注的未来研究方向包括:

1. 理论分析:深入研究GFlowNet的收敛性和泛化性能。
2. 架构改进:设计更高效的神经网络架构,以处理更复杂的问题。
3. 应用拓展:将GFlowNet应用到更广泛的领域,如材料设计、蛋白质工程等。
4. 与其他方法结合:探索GFlowNet与其他机器学习方法(如变分推断、元学习等)的结合。

结论

GFlowNet作为一种新兴的生成式模型框架,为解决复杂的离散优化问题提供了强大的工具。它在分子设计等领域已经展现出了巨大的潜力,能够生成多样化的高质量样本,并有效探索未知的高奖励区域。随着研究的深入和应用的拓展,GFlowNet有望在科学发现和工程优化等多个领域产生重要影响。

对于研究人员和实践者来说,深入了解GFlowNet的原理和应用,并探索其在具体问题中的潜力,将是一个充满机遇的方向。随着开源工具和资源的不断丰富,GFlowNet的应用门槛也在不断降低,为更多创新应用的出现创造了条件。