LTSF-Linear: 一种高效的长期时间序列预测线性模型

LTSF-Linear简介

LTSF-Linear是由香港中文大学的研究团队在2023年AAAI会议上提出的一种用于长期时间序列预测(Long-Term Time Series Forecasting, LTSF)的线性模型。该模型虽然结构简单,仅由一层或两层线性层组成,但在多个基准数据集上的性能却显著超越了包括Transformer在内的多种复杂模型。

LTSF-Linear的提出源于研究人员对这样一个问题的思考:在长期时间序列预测任务中,Transformer等复杂模型真的是必需的吗?通过大量实验,他们发现简单的线性模型不仅能够达到甚至超越Transformer的性能,而且具有更高的计算效率和更好的可解释性。

LTSF-Linear模型家族

LTSF-Linear实际上是一个模型家族,包含三个变体:

1. Linear: 最基础的版本,仅由一个线性层组成。
2. NLinear: 在Linear的基础上增加了简单的归一化处理,以应对训练集和测试集分布不一致的情况。
3. DLinear: 结合了分解策略,将输入数据分解为趋势和季节性两个组件,分别用线性层处理后再合并。

这三个模型虽然结构简单,但都具有一些共同的优势:

• O(1)的最大信号传播路径长度,能够有效捕捉短期和长期的时间依赖关系。
• 高效率:由于只有一层或两层线性层,模型参数少,内存占用低,推理速度快。
• 可解释性强:训练后可以直观地可视化权重,了解模型的预测依据。
• 易用性高:无需复杂的超参数调优即可使用。

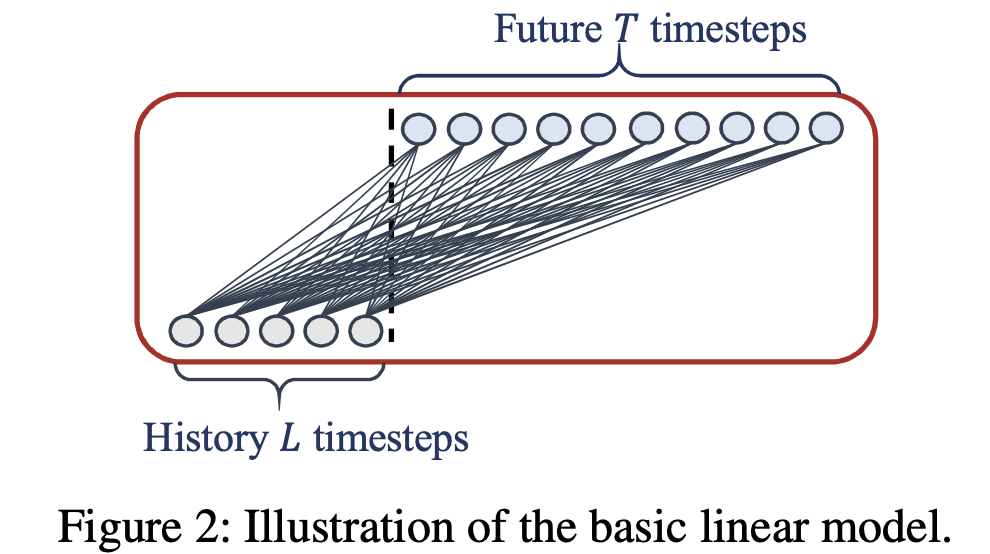
与Transformer类模型的对比

研究人员将LTSF-Linear与多个基于Transformer的模型进行了对比,包括:

• 原始Transformer (NeurIPS 2017)
• Informer (AAAI 2021 最佳论文)
• Autoformer (NeurIPS 2021)
• Pyraformer (ICLR 2022 Oral)
• FEDformer (ICML 2022)

实验结果显示,在多个长期时间序列预测基准数据集上,LTSF-Linear以显著优势超越了这些复杂的Transformer模型。

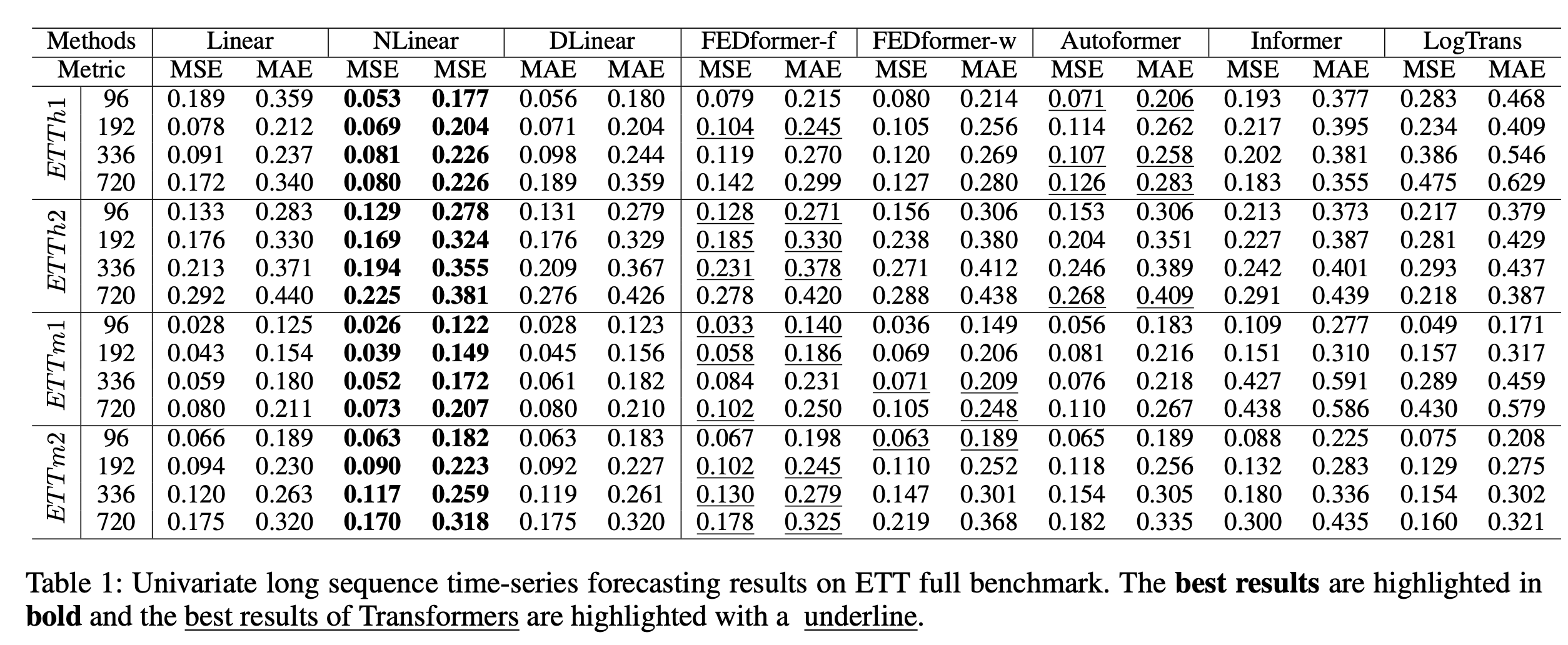
从上图的单变量预测结果对比可以看出,LTSF-Linear家族的三个模型(DLinear、Linear、NLinear)在各个指标上都明显优于Transformer类模型。特别是在Exchange Rate和Weather数据集上,LTSF-Linear的优势更为明显。

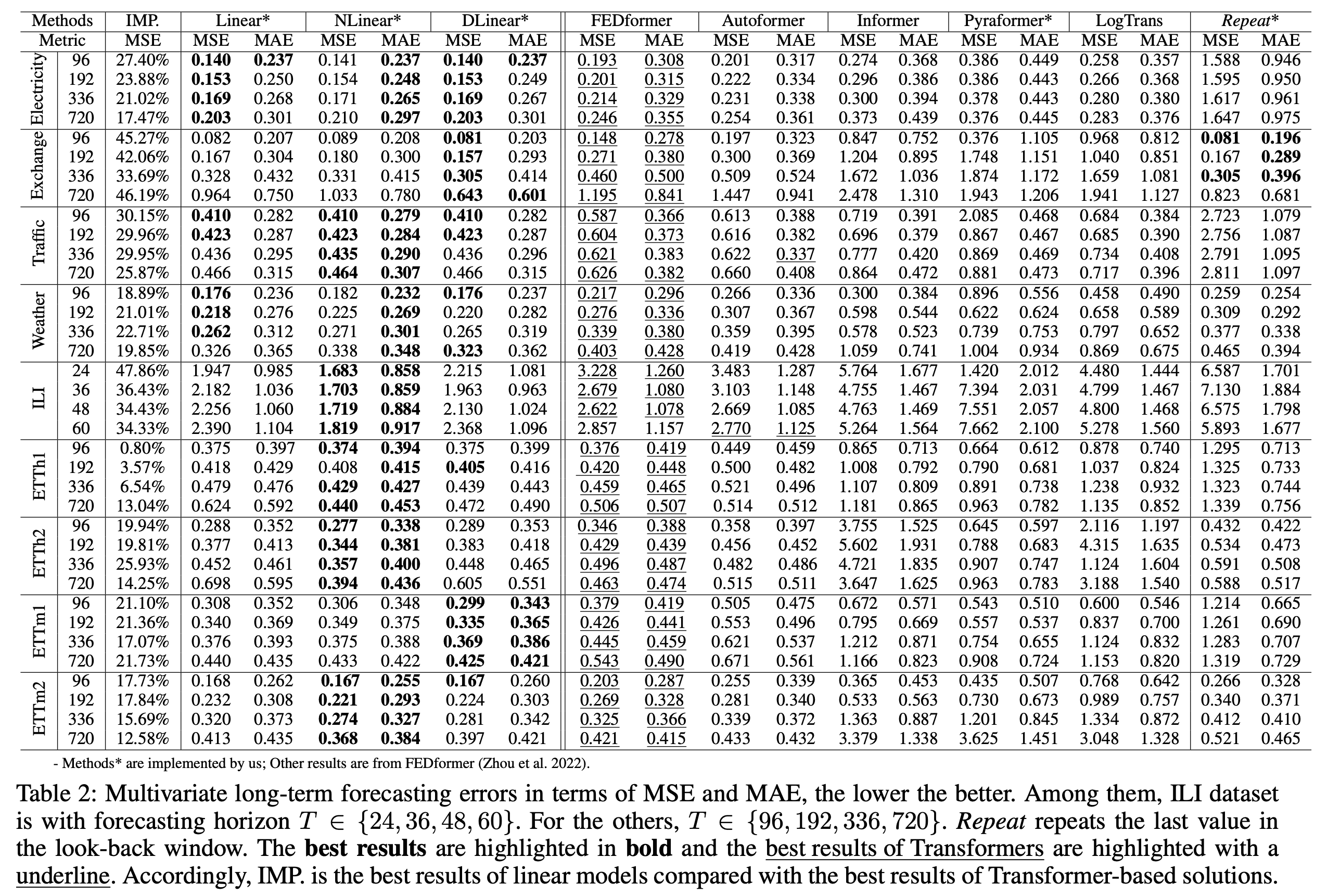
多变量预测的结果同样显示了LTSF-Linear的优越性。在所有数据集上,LTSF-Linear都取得了最佳或接近最佳的性能。这一结果令人惊讶,因为传统观点认为复杂的Transformer结构更适合处理多变量之间的复杂关系。

LTSF-Linear的效率优势

除了预测性能外,LTSF-Linear在计算效率方面也具有显著优势。研究人员对比了LTSF-Linear与Transformer模型在参数量、MAC(乘加操作数)和推理时间上的差异:

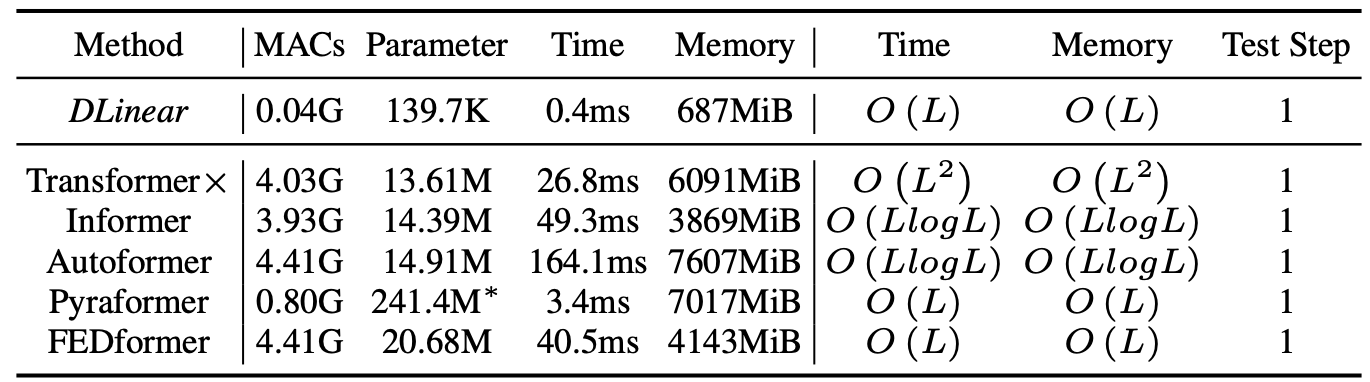
从表格中可以看出,LTSF-Linear (以DLinear为例)的参数量仅为Transformer的0.1%,MAC操作数约为1%,而推理速度快了近100倍。这意味着LTSF-Linear不仅在预测性能上占优,在实际应用中也能带来巨大的资源节省和效率提升。

LTSF-Linear的可解释性

LTSF-Linear的另一大优势是其良好的可解释性。由于模型结构简单,我们可以直接可视化其权重,从而了解模型是如何进行预测的。

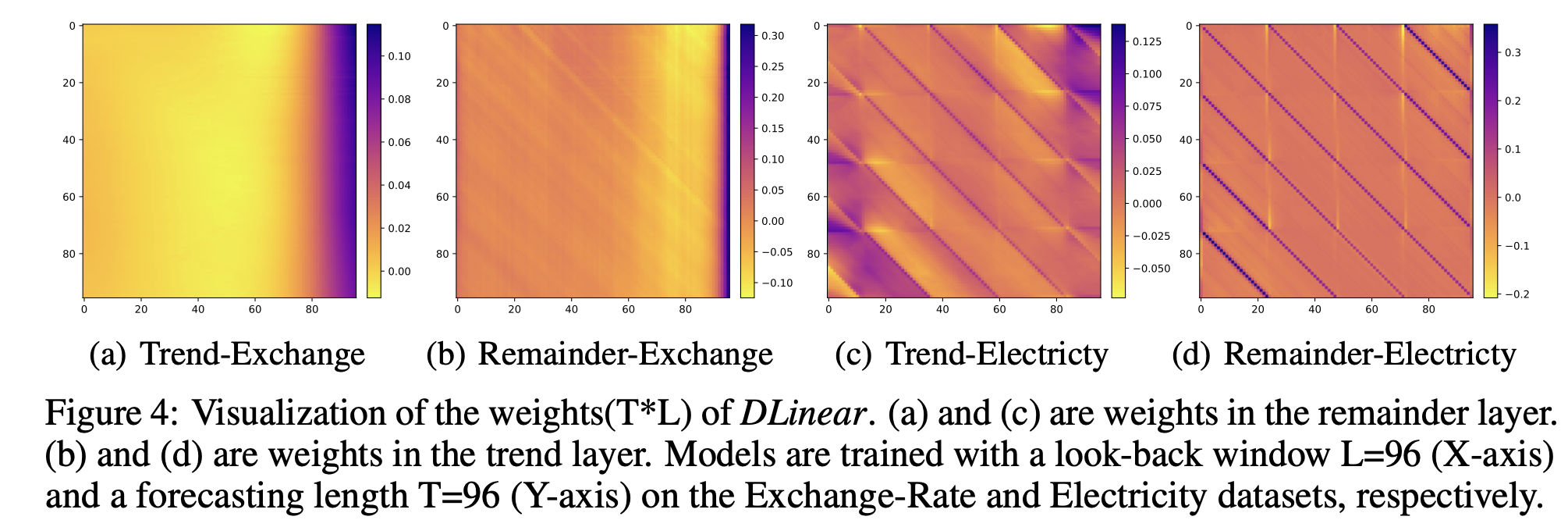
上图展示了DLinear模型在不同数据集上的权重可视化结果。我们可以清晰地看到权重呈现出的周期性模式,这与时间序列数据本身的周期性特征相对应。这种直观的可解释性使得研究人员和实践者能更好地理解模型的工作原理,有助于进一步改进模型和解释预测结果。

LTSF-Linear的影响与展望

LTSF-Linear的成功为时间序列预测领域带来了新的思考:

1. 模型复杂度与任务的匹配:在某些任务中,简单模型可能比复杂模型更有效。这提醒我们在选择模型时要充分考虑任务本身的特性。

2. 归纳偏置的重要性:LTSF-Linear的成功部分归功于其线性结构所隐含的归纳偏置,这与时间序列数据的特性高度契合。这启示我们在设计模型时应更多地考虑数据的内在特性。

3. 效率与可解释性的平衡:LTSF-Linear证明了在保持高性能的同时,也可以实现高效率和良好的可解释性。这对于实际应用具有重要意义。

4. 研究方向的反思:LTSF-Linear的成功可能会促使研究人员重新审视当前在模型复杂化方面的努力,转而探索如何设计更加简洁高效的模型结构。

展望未来,LTSF-Linear为时间序列预测领域开辟了新的研究方向:

1. 模型改进:虽然LTSF-Linear已经表现出色,但仍有进一步优化的空间。例如,探索更有效的数据分解方法,或结合其他简单而有效的技术。

2. 理论分析:深入研究LTSF-Linear成功的理论基础,可能会为时间序列建模提供新的洞见。

3. 应用拓展:将LTSF-Linear应用到更多领域,如金融预测、能源消耗预测等,并根据具体应用场景进行优化。

4. 与其他方法的结合:探索将LTSF-Linear与其他先进技术(如神经常微分方程)结合的可能性,以应对更复杂的预测任务。

总的来说,LTSF-Linear的提出为时间序列预测领域带来了新的活力和思路。它不仅提供了一个高效、有效的预测工具,也促使我们重新思考模型设计的原则和方向。随着进一步的研究和应用,LTSF-Linear有望在学术界和工业界产生更广泛的影响。