懂AI

数值线性代数:高效矩阵计算的艺术

RayRay
线性代数数值分解Python教程数据科学Github开源项目

数值线性代数:高效矩阵计算的艺术

数值线性代数是计算数学和科学计算中的一个重要分支,主要研究如何用计算机高效、准确地进行矩阵运算。它结合了线性代数的理论基础和数值分析的计算方法,为解决大规模科学和工程问题提供了强大的工具。

数值线性代数的基本问题

数值线性代数主要关注以下几个基本问题:

  1. 如何高效地进行矩阵-向量乘法和矩阵-矩阵乘法
  2. 如何求解线性方程组Ax = b
  3. 如何计算矩阵的特征值和特征向量
  4. 如何进行矩阵分解,如LU分解、QR分解、奇异值分解(SVD)等
  5. 如何处理病态问题和提高数值稳定性

这些问题看似简单,但在处理大规模矩阵时会变得极具挑战性。数值线性代数的目标就是设计高效算法来解决这些问题,同时保证计算结果的准确性。

主要算法和技术

数值线性代数发展了许多重要的算法和技术,包括:

  1. 高斯消元法:求解线性方程组的经典方法
  2. LU分解:将矩阵分解为上三角和下三角矩阵的乘积
  3. QR分解:将矩阵分解为正交矩阵和上三角矩阵的乘积
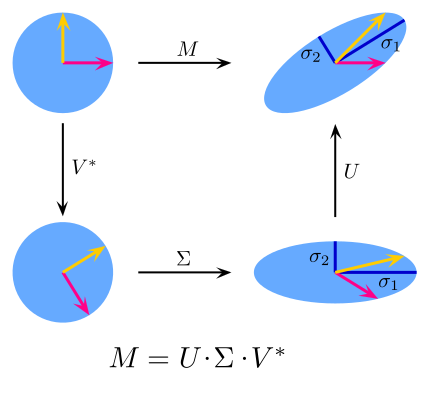
  4. 奇异值分解(SVD):将矩阵分解为左奇异向量、奇异值和右奇异向量
  5. 幂法和QR算法:计算矩阵特征值的迭代方法
  6. Krylov子空间方法:求解大规模稀疏线性系统
  7. 快速傅里叶变换(FFT):高效计算离散傅里叶变换

这些算法构成了数值线性代数的核心,为解决各种实际问题提供了基础。

SVD decomposition

应用领域

数值线性代数在科学和工程中有广泛的应用,包括但不限于:

  1. 图像和信号处理:压缩感知、主成分分析等
  2. 机器学习:线性回归、降维、矩阵分解等
  3. 计算流体力学:有限元方法求解偏微分方程
  4. 结构分析:大型结构的应力和变形计算
  5. 量子化学:电子结构计算
  6. 网络分析:PageRank算法等
  7. 金融工程:投资组合优化、风险管理等

在这些领域中,高效的数值线性代数算法往往是解决大规模问题的关键。

面临的挑战

尽管数值线性代数取得了巨大进展,但仍面临一些重要挑战:

  1. 超大规模问题:随着数据规模的不断增长,如何处理超大矩阵成为一个关键问题
  2. 高维数据:在机器学习等领域,如何有效处理高维数据的计算问题
  3. 并行计算:如何设计能充分利用现代并行计算架构的算法
  4. 数值稳定性:如何在有限精度计算中保证结果的准确性
  5. 非线性问题:如何将线性代数方法扩展到非线性问题

这些挑战推动着数值线性代数领域不断发展创新。

Parallel matrix multiplication

最新进展

近年来,数值线性代数领域出现了一些重要的新进展:

  1. 随机化算法:利用随机采样等技术加速大规模矩阵计算
  2. 张量方法:将矩阵方法推广到高阶张量,用于处理多维数据
  3. 图形处理器(GPU)计算:利用GPU的并行计算能力加速矩阵运算
  4. 量子算法:探索量子计算在线性代数问题上的潜力
  5. 机器学习方法:将深度学习等技术应用于求解线性代数问题

这些新方法为解决更大规模、更复杂的问题提供了新的可能性。

学习资源

对于想深入学习数值线性代数的读者,以下是一些优质资源:

  1. 教材:《Numerical Linear Algebra》by Trefethen and Bau
  2. 在线课程:fast.ai的Computational Linear Algebra课程
  3. 软件包:LAPACK、Eigen、NumPy等
  4. 开源项目:Julia语言的线性代数库

通过系统学习和实践,读者可以掌握这一强大工具,并将其应用到各自的研究或工作中。

数值线性代数是一个充满活力的研究领域,它不断推动着科学计算和数据科学的发展。随着问题规模的增长和新技术的出现,这一领域必将继续发挥重要作用,为解决复杂的科学和工程问题提供强大支持。无论是研究人员还是实践者,掌握数值线性代数的核心概念和技术都将大有裨益。

编辑推荐精选

AEE

AEE

AI Excel全自动制表工具

AEE 在线 AI 全自动 Excel 编辑器，提供智能录入、自动公式、数据整理、图表生成等功能，高效处理 Excel 任务，提升办公效率。支持自动高亮数据、批量计算、不规则数据录入，适用于企业、教育、金融等多场景。

UI-TARS-desktop

UI-TARS-desktop

基于 UI-TARS 视觉语言模型的桌面应用，可通过自然语言控制计算机进行多模态操作。

UI-TARS-desktop 是一款功能强大的桌面应用，基于 UI-TARS（视觉语言模型）构建。它具备自然语言控制、截图与视觉识别、精确的鼠标键盘控制等功能，支持跨平台使用（Windows/MacOS），能提供实时反馈和状态显示，且数据完全本地处理，保障隐私安全。该应用集成了多种大语言模型和搜索方式，还可进行文件系统操作。适用于需要智能交互和自动化任务的场景，如信息检索、文件管理等。其提供了详细的文档，包括快速启动、部署、贡献指南和 SDK 使用说明等，方便开发者使用和扩展。

Wan2.1

Wan2.1

开源且先进的大规模视频生成模型项目

Wan2.1 是一个开源且先进的大规模视频生成模型项目，支持文本到图像、文本到视频、图像到视频等多种生成任务。它具备丰富的配置选项，可调整分辨率、扩散步数等参数，还能对提示词进行增强。使用了多种先进技术和工具，在视频和图像生成领域具有广泛应用前景，适合研究人员和开发者使用。

爱图表

爱图表

全流程 AI 驱动的数据可视化工具，助力用户轻松创作高颜值图表

爱图表（aitubiao.com）就是AI图表，是由镝数科技推出的一款创新型智能数据可视化平台，专注于为用户提供便捷的图表生成、数据分析和报告撰写服务。爱图表是中国首个在图表场景接入DeepSeek的产品。通过接入前沿的DeepSeek系列AI模型，爱图表结合强大的数据处理能力与智能化功能，致力于帮助职场人士高效处理和表达数据，提升工作效率和报告质量。

Qwen2.5-VL

Qwen2.5-VL

一款强大的视觉语言模型，支持图像和视频输入

Qwen2.5-VL 是一款强大的视觉语言模型，支持图像和视频输入，可用于多种场景，如商品特点总结、图像文字识别等。项目提供了 OpenAI API 服务、Web UI 示例等部署方式，还包含了视觉处理工具，有助于开发者快速集成和使用，提升工作效率。

HunyuanVideo

HunyuanVideo

HunyuanVideo 是一个可基于文本生成高质量图像和视频的项目。

HunyuanVideo 是一个专注于文本到图像及视频生成的项目。它具备强大的视频生成能力，支持多种分辨率和视频长度选择，能根据用户输入的文本生成逼真的图像和视频。使用先进的技术架构和算法，可灵活调整生成参数，满足不同场景的需求，是文本生成图像视频领域的优质工具。

WebUI for Browser Use

WebUI for Browser Use

一个基于 Gradio 构建的 WebUI，支持与浏览器智能体进行便捷交互。

WebUI for Browser Use 是一个强大的项目，它集成了多种大型语言模型，支持自定义浏览器使用，具备持久化浏览器会话等功能。用户可以通过简洁友好的界面轻松控制浏览器智能体完成各类任务，无论是数据提取、网页导航还是表单填写等操作都能高效实现，有利于提高工作效率和获取信息的便捷性。该项目适合开发者、研究人员以及需要自动化浏览器操作的人群使用，在 SEO 优化方面，其关键词涵盖浏览器使用、WebUI、大型语言模型集成等，有助于提高网页在搜索引擎中的曝光度。

xiaozhi-esp32

xiaozhi-esp32

基于 ESP32 的小智 AI 开发项目，支持多种网络连接与协议，实现语音交互等功能。

xiaozhi-esp32 是一个极具创新性的基于 ESP32 的开发项目，专注于人工智能语音交互领域。项目涵盖了丰富的功能，如网络连接、OTA 升级、设备激活等，同时支持多种语言。无论是开发爱好者还是专业开发者，都能借助该项目快速搭建起高效的 AI 语音交互系统，为智能设备开发提供强大助力。

olmocr

olmocr

一个用于 OCR 的项目，支持多种模型和服务器进行 PDF 到 Markdown 的转换，并提供测试和报告功能。

olmocr 是一个专注于光学字符识别（OCR）的 Python 项目，由 Allen Institute for Artificial Intelligence 开发。它支持多种模型和服务器，如 vllm、sglang、OpenAI 等，可将 PDF 文件的页面转换为 Markdown 格式。项目还提供了测试框架和 HTML 报告生成功能，方便用户对 OCR 结果进行评估和分析。适用于科研、文档处理等领域，有助于提高工作效率和准确性。

飞书多维表格

飞书多维表格

飞书多维表格 ×DeepSeek R1 满血版

飞书多维表格联合 DeepSeek R1 模型，提供 AI 自动化解决方案，支持批量写作、数据分析、跨模态处理等功能，适用于电商、短视频、影视创作等场景，提升企业生产力与创作效率。关键词：飞书多维表格、DeepSeek R1、AI 自动化、批量处理、企业协同工具。

下拉加载更多