Universal Numbers Library: 多格式可变精度算术库

Universal Numbers Library简介

Universal Numbers Library是一个强大的C++模板库,提供了丰富的自定义算术类型,旨在支持混合精度算法的开发和优化。该库特别适用于人工智能、机器学习、计算机视觉、信号处理等领域,可以帮助开发者根据应用需求定制精度和动态范围,从而提高性能和能源效率。

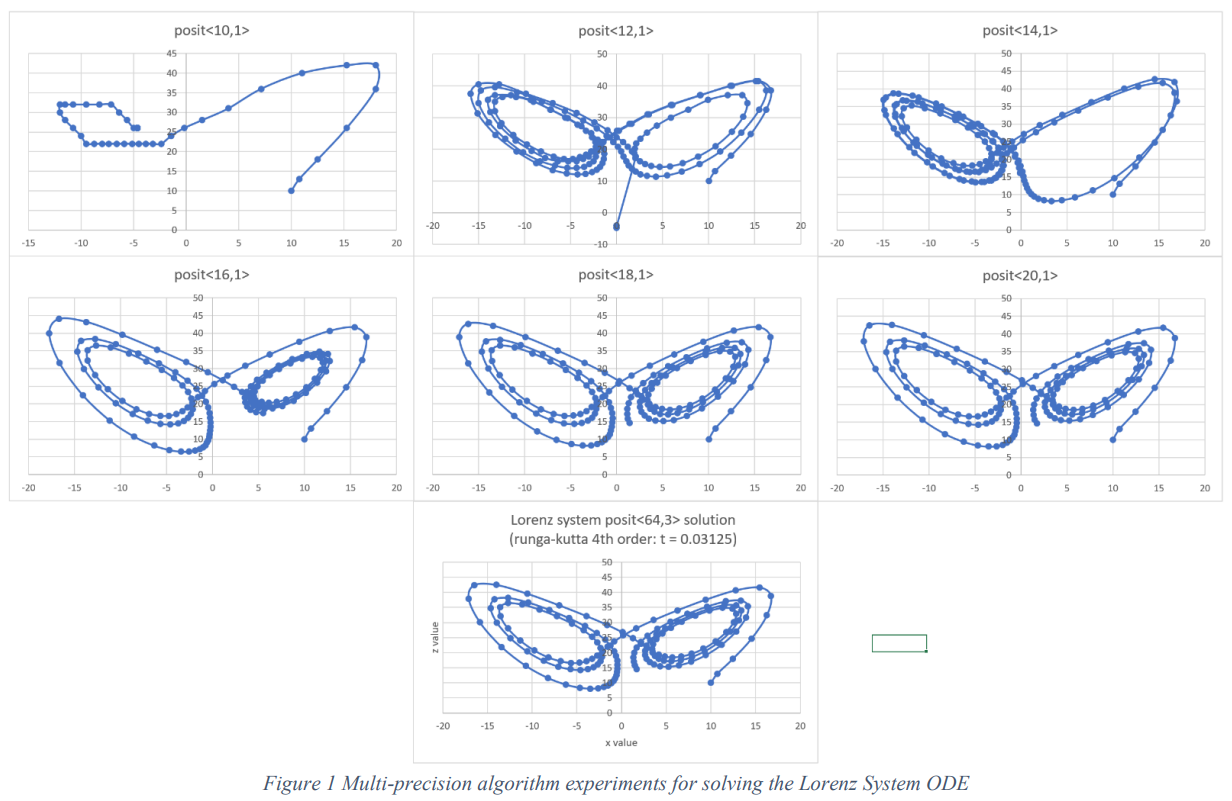
Universal Library Logo

主要特点

提供多种数字系统:包括整数、小数、定点数、浮点数、对数数等。
即插即用:可以作为原生类型的替代品,方便探索IEEE-754浮点数的替代方案。
纯头文件库:无需额外依赖,易于集成到现有项目中。
灵活配置:支持静态和弹性整数、小数、定点数、有理数、线性浮点数等多种格式。
性能优化:针对嵌入式应用进行了优化,可显著提升AI算法的性能。

使用示例

#include <universal/number/cfloat/cfloat.hpp>

// 定义计算内核
template<typename Real>
Real MyKernel(const Real& a, const Real& b) {
    return a * b;  
}

constexpr double pi = 3.14159265358979323846;

int main() {
    using Real = sw::universal::half; // 半精度IEEE-754浮点数  

    Real a = sqrt(2);
    Real b = pi;
    std::cout << "Result: " << MyKernel(a, b) << std::endl;  
}

如何构建和安装

Universal Numbers Library使用CMake构建系统。推荐使用CMake 3.23或更高版本。

基本构建步骤:

git clone https://github.com/stillwater-sc/universal
cd universal
mkdir build && cd build
cmake ..
make -j $(nproc)
make test

对于Windows和Visual Studio用户,可以使用CMakePredefinedTargets:

ALL_BUILD: 编译所有项目
INSTALL: 安装Universal库
RUN_TESTS: 运行所有测试

构建选项

可以通过CMake选项控制构建内容,例如:

cmake -DBUILD_EDUCATION=OFF -DBUILD_NUMBER_POSITS=ON ..

常用选项包括:

BUILD_ALL: 构建所有组件
BUILD_EDUCATION: 构建教育示例
BUILD_NUMBER_XXX: 构建特定数字系统(如POSITS)
USE_AVX2: 启用AVX2指令集优化

命令行工具

Universal库提供了一系列有用的命令行工具,用于检查原生IEEE浮点类型和自定义数字系统:

ieee: 显示IEEE浮点值的组成部分
quarter/half/single/double/longdouble/quad: 显示不同精度IEEE-754值的组件和特征
signedint/unsignedint: 显示有符号/无符号整数的组件和特征
fixpnt/posit/lns: 显示定点数/posit/对数数系统值的组件和特征

例如:

$ ieee 1.234567890123456789012
compiler              : 7.5.0
float precision       : 23 bits
double precision      : 52 bits
long double precision : 63 bits

Decimal representations
input value:             1.23456789012
      float:                1.23456788
     double:        1.2345678901199999
long double:    1.23456789011999999999

...```

这些工具可以帮助开发者快速了解不同数字系统的特性和表示方式。

## 在混合精度算法研究中应用Universal库

为了快速启动混合精度算法开发和优化项目,Universal提供了一个GitHub模板仓库[mpadao-template](https://github.com/stillwater-sc/mpadao-template)。该模板包含完整的开发环境设置,包括依赖库、开发容器、VS Code集成和GitHub CI工作流。

使用这个模板是开始使用Universal进行混合精度算法开发的最简单方法。

## Universal库的动机

现代深度学习AI应用对性能和功耗提出了极高的要求。传统的IEEE-754浮点格式在满足AI应用的性能和功耗需求方面已经显得力不从心。Google和Microsoft等公司已经放弃使用传统浮点格式,转而采用更适合AI的数字系统,以获得两个数量级的性能提升。

除AI外,云计算、物联网、嵌入式系统和高性能计算等领域也面临着类似的挑战。采用新的数字系统可能会使这些应用的规模和成本得到数量级的改善。

IEEE-754浮点格式存在以下问题:

1. 浪费的位模式:32位浮点数有约800万种表示NaN的方式,64位浮点数更是有2千兆种。

2. 数学不正确:规定了正零和负零,导致结合律和分配律的丢失。

3. 溢出和下溢:溢出到±∞会导致相对误差无限增大,下溢到0会丢失符号信息。

4. 未使用的动态范围:双精度浮点的动态范围高达2^2047,而大多数数值软件都围绕1.0工作。

5. 复杂的电路:非规格化浮点数需要特殊处理,增加了硬件实现的复杂性。

6. 缺乏渐进溢出和固定精度:IEEE浮点数除非规格化数外,精度是固定的。

相比之下,posit数字系统克服了这些缺点:

1. 经济:没有冗余的位模式,只有一种表示∞和0的方式。

2. 保留数学特性:只有一种表示零的方式,编码围绕1.0对称。通过quire支持结合律和分配律。

3. 渐进溢出和下溢:在整个数值范围内提供渐进的精度变化。

4. 简化的硬件:不需要特殊处理非规格化数,简化了硬件实现。

5. 可调节的动态范围:可以根据应用需求调整动态范围。

Universal库提供了包括posit在内的多种数字系统的实现,让开发者可以根据应用需求选择最合适的数字表示方式,从而获得更好的性能、精度和能效。

## 结论

Universal Numbers Library为混合精度算法开发提供了强大而灵活的工具集。通过支持多种数字系统和精度,它使开发者能够根据特定应用的需求定制算术类型,从而在性能、精度和能效之间取得最佳平衡。无论是在AI、信号处理、科学计算还是嵌入式系统领域,Universal库都为创新和优化打开了新的可能性。

随着计算需求的不断增长和对能效的日益关注,像Universal这样的库将在未来的计算架构中扮演越来越重要的角色。它不仅提供了替代传统IEEE-754浮点数的选择,更为数值计算的未来发展指明了方向。

对于希望深入探索数字系统或优化算法性能的研究人员和开发者来说,Universal Numbers Library无疑是一个值得关注和使用的强大工具。通过其丰富的文档、示例和工具,开发者可以快速上手并在自己的项目中应用这些先进的数字系统概念。

Universal Numbers Library的开源性质也为社区贡献和协作创造了条件。随着更多开发者的参与,我们可以期待看到更多创新的数字系统和优化技术的出现,进一步推动计算技术的发展。

总之,Universal Numbers Library代表了数值计算的未来趋势,为追求极致性能和精度的应用开辟了新的可能性。无论是在学术研究还是工业应用中,它都将是一个不可或缺的工具,值得每一个对数值计算感兴趣的开发者深入探索和使用。