neurodiffeq

引用

@article{chen2020neurodiffeq,
  title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
  author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
  journal={Journal of Open Source Software},
  volume={5},
  number={46},
  pages={1931},
  year={2020}
}

🔥🔥🔥你知道吗？neurodiffeq支持解决方案包并可用于解决反向问题！点击这里查看！

:mortar_board: 已经熟悉neurodiffeq了吗？ :point_down: 跳转到常见问题。

简介

neurodiffeq是一个使用神经网络求解微分方程的软件包。微分方程是将某个函数与其导数相关联的方程。它们在各种科学和工程领域中出现。传统上，这些问题可以通过数值方法（如有限差分、有限元）来解决。虽然这些方法有效且足够，但它们的表达能力受到函数表示的限制。如果我们能够计算出连续且可微的微分方程解，那将会很有意思。

作为通用函数逼近器，人工神经网络已被证明具有解决具有特定初始/边界条件的常微分方程（ODE）和偏微分方程（PDE）的潜力。neurodiffeq的目标是实现这些使用ANN求解微分方程的现有技术，使软件具有足够的灵活性，可以处理各种用户定义的问题。

安装

使用pip

与大多数标准库一样，neurodiffeq托管在PyPI上。要安装最新的稳定版本，请运行：

pip install -U neurodiffeq  # '-U'表示更新到最新版本

手动安装

或者，你可以手动安装库以获取我们新功能的早期访问权。这是希望为库做出贡献的开发者推荐的方式。

git clone https://github.com/NeuroDiffGym/neurodiffeq.git
cd neurodiffeq && pip install -r requirements
pip install .  # 如果要对库进行更改，请使用`pip install -e .`
pytest tests/  # 运行测试。可选。

入门

我们很乐意解答你的任何问题。同时，你可以查看常见问题。

要查看neurodiffeq的完整教程和文档，请查看官方文档。

除了文档之外，我们最近还制作了一个快速入门的演示视频和幻灯片。

使用示例

导入

from neurodiffeq import diff
from neurodiffeq.solvers import Solver1D, Solver2D
from neurodiffeq.conditions import IVP, DirichletBVP2D
from neurodiffeq.networks import FCNN, SinActv

ODE系统示例

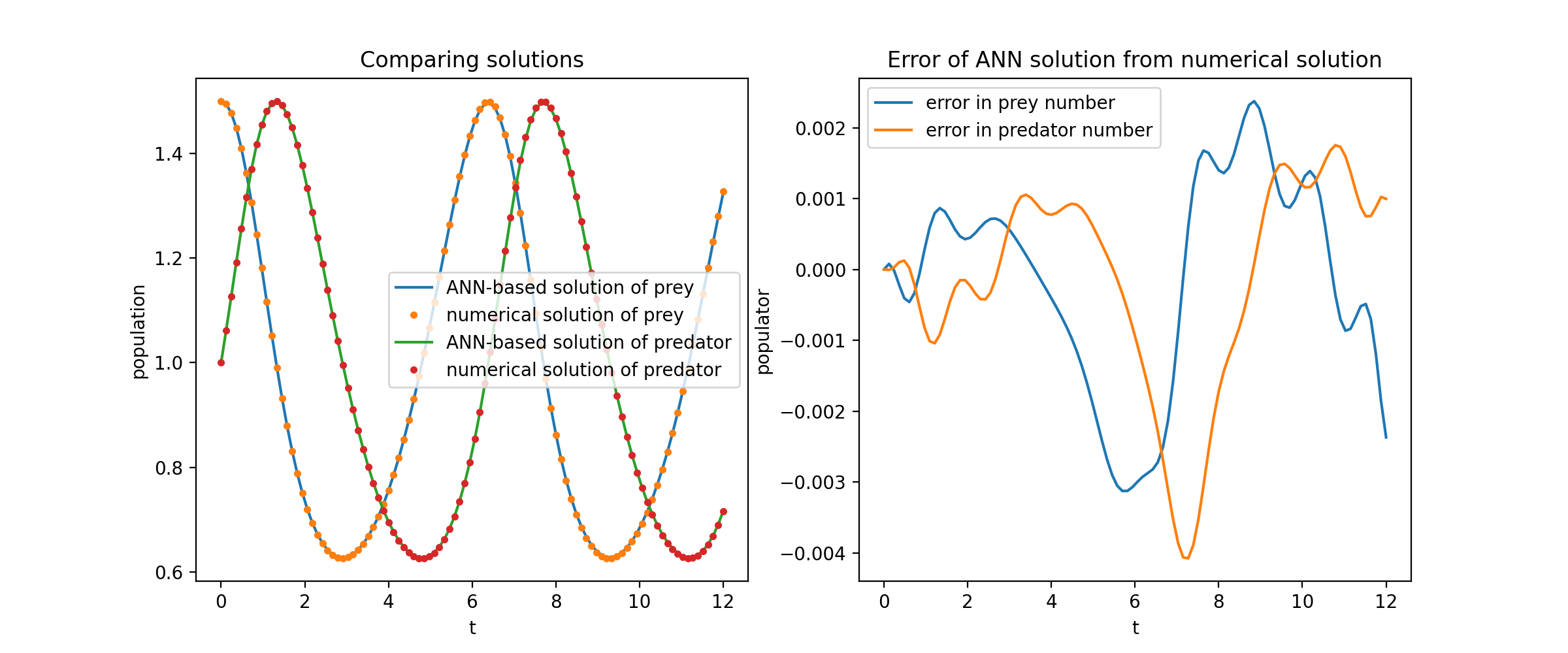
这里我们解决一个非线性的两个ODE系统，称为Lotka–Volterra方程。有两个未知函数（u和v）和一个独立变量（t）。

def ode_system(u, v, t): 
    return [diff(u,t)-(u-u*v), diff(v,t)-(u*v-v)]

conditions = [IVP(t_0=0.0, u_0=1.5), IVP(t_0=0.0, u_0=1.0)]
nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]

solver = Solver1D(ode_system, conditions, t_min=0.1, t_max=12.0, nets=nets)
solver.fit(max_epochs=3000)
solution = solver.get_solution()

solution是一个可调用对象，你可以向它传递numpy数组或torch张量，如：

u, v = solution(t, to_numpy=True)  # t可以是np.ndarray或torch.Tensor

将u和v与它们的解析解进行对比绘图，得到类似这样的结果：

PDE系统示例

这里我们在一个矩形上解带有Dirichlet边界条件的拉普拉斯方程。注意，我们选择拉普拉斯方程是因为它计算解析解的简单性。在实际应用中，你可以尝试任何非线性、混沌的PDE，只要你能够充分调整求解器。

求解2-D PDE系统与求解ODE非常相似，只是边值问题有两个变量x和y，或者初始边值问题有x和t，这两种情况都支持。

def pde_system(u, x, y):
    return [diff(u, x, order=2) + diff(u, y, order=2)]
conditions = [
    DirichletBVP2D(
        x_min=0, x_min_val=lambda y: torch.sin(np.pi*y),
        x_max=1, x_max_val=lambda y: 0,                   
        y_min=0, y_min_val=lambda x: 0,                   
        y_max=1, y_max_val=lambda x: 0,                   
    )
]
nets = [FCNN(n_input_units=2, n_output_units=1, hidden_units=(512,))]

solver = Solver2D(pde_system, conditions, xy_min=(0, 0), xy_max=(1, 1), nets=nets)
solver.fit(max_epochs=2000)
solution = solver.get_solution()

二维偏微分方程的solution签名与常微分方程略有不同。同样，它接受NumPy数组或PyTorch张量作为输入。

u = solution(x, y, to_numpy=True)

在[0,1] × [0,1]区间上评估u得到以下图形

基于ANN的解	PDE的残差

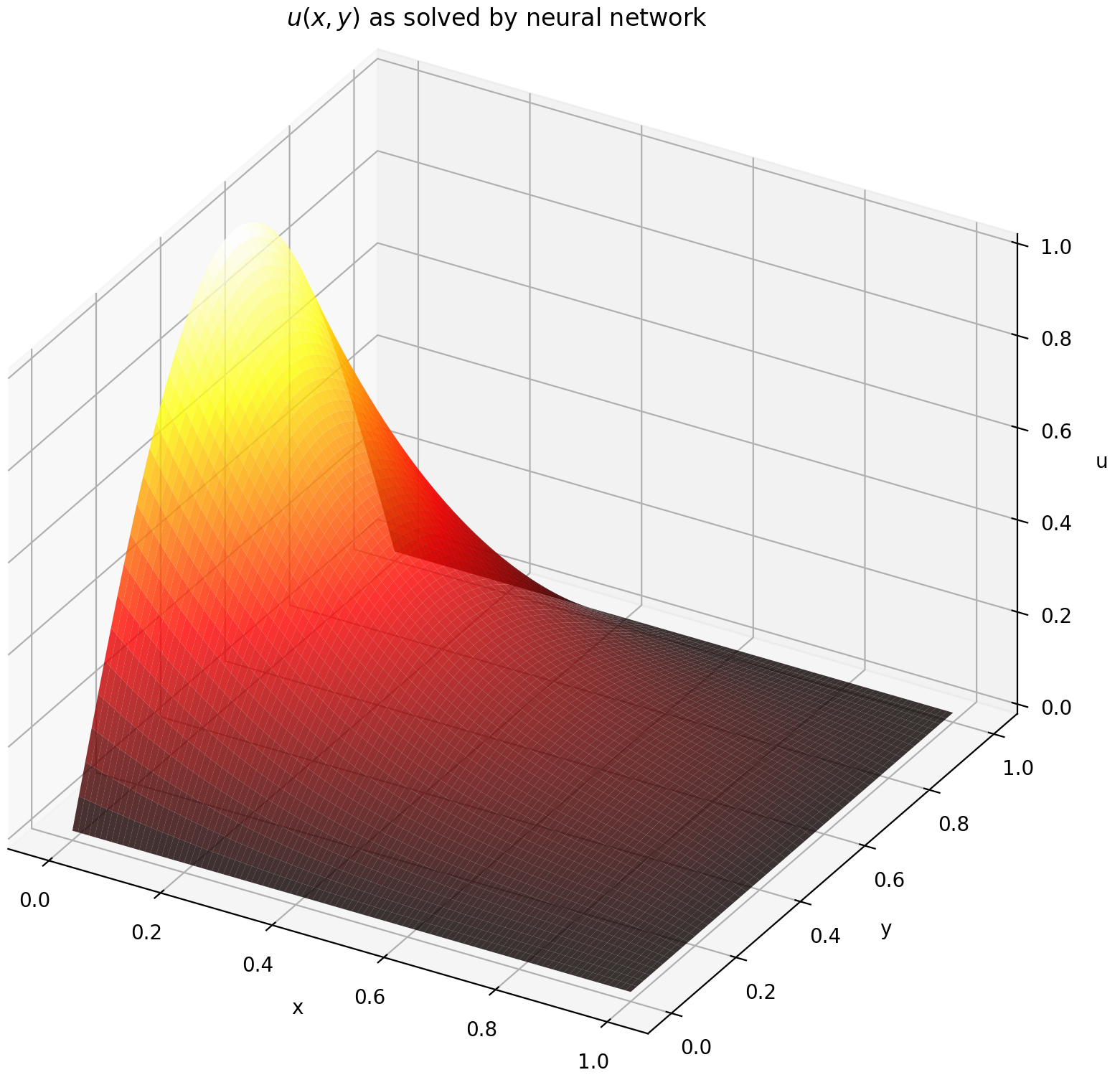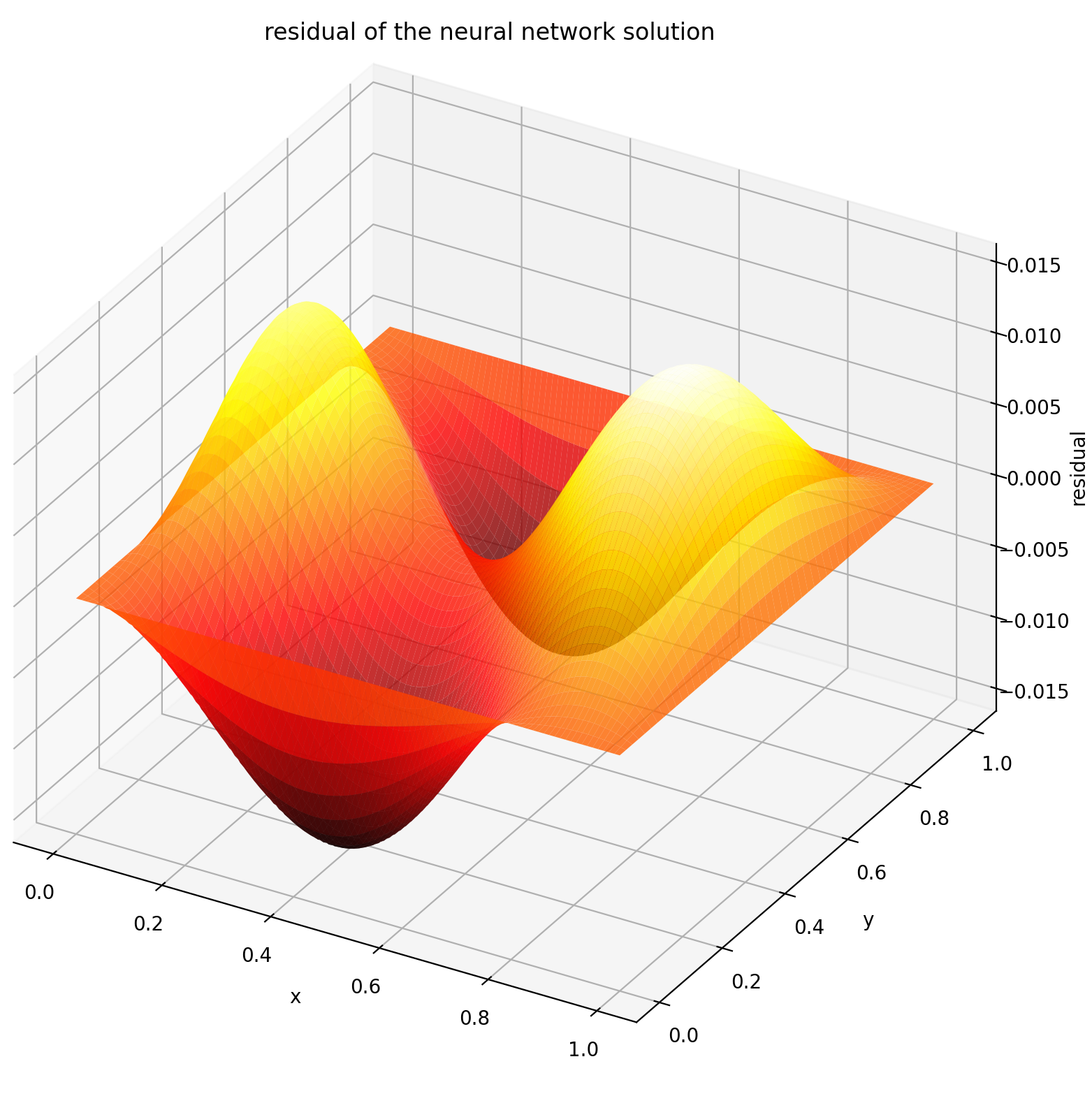使用监视器

监视器是一种用于可视化PDE/ODE解以及训练过程中损失和自定义指标历史的工具。Jupyter Notebook用户需要运行%matplotlib notebook魔法命令。对于Jupyter Lab用户，请尝试%matplotlib widget。

from neurodiffeq.monitors import Monitor1D
...
monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)
solver.fit(..., callbacks=[monitor.to_callback()])

您应该会看到图形每100个epoch更新一次，以及在最后一个epoch更新，显示两个图表——一个用于在[0,12]区间上的解可视化，另一个用于损失历史（训练和验证）。

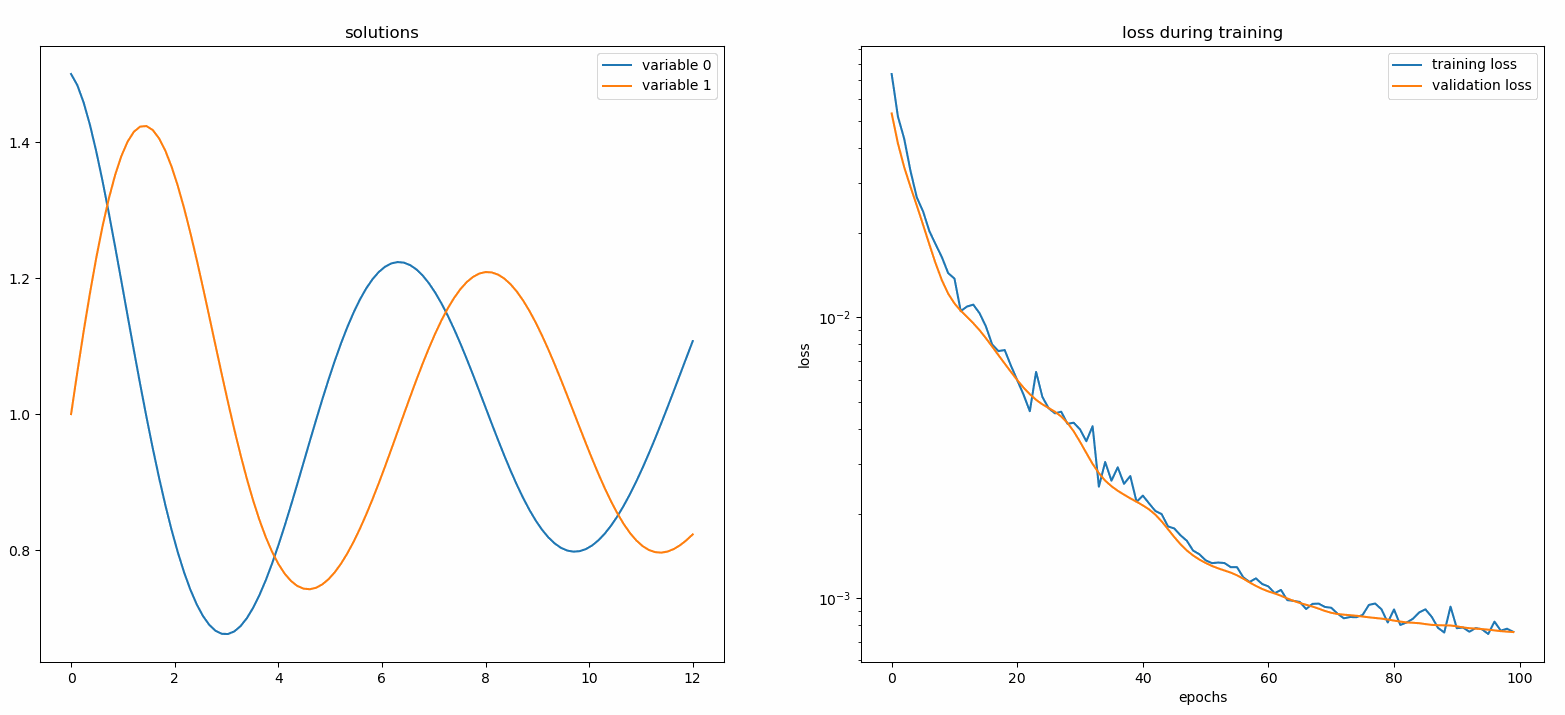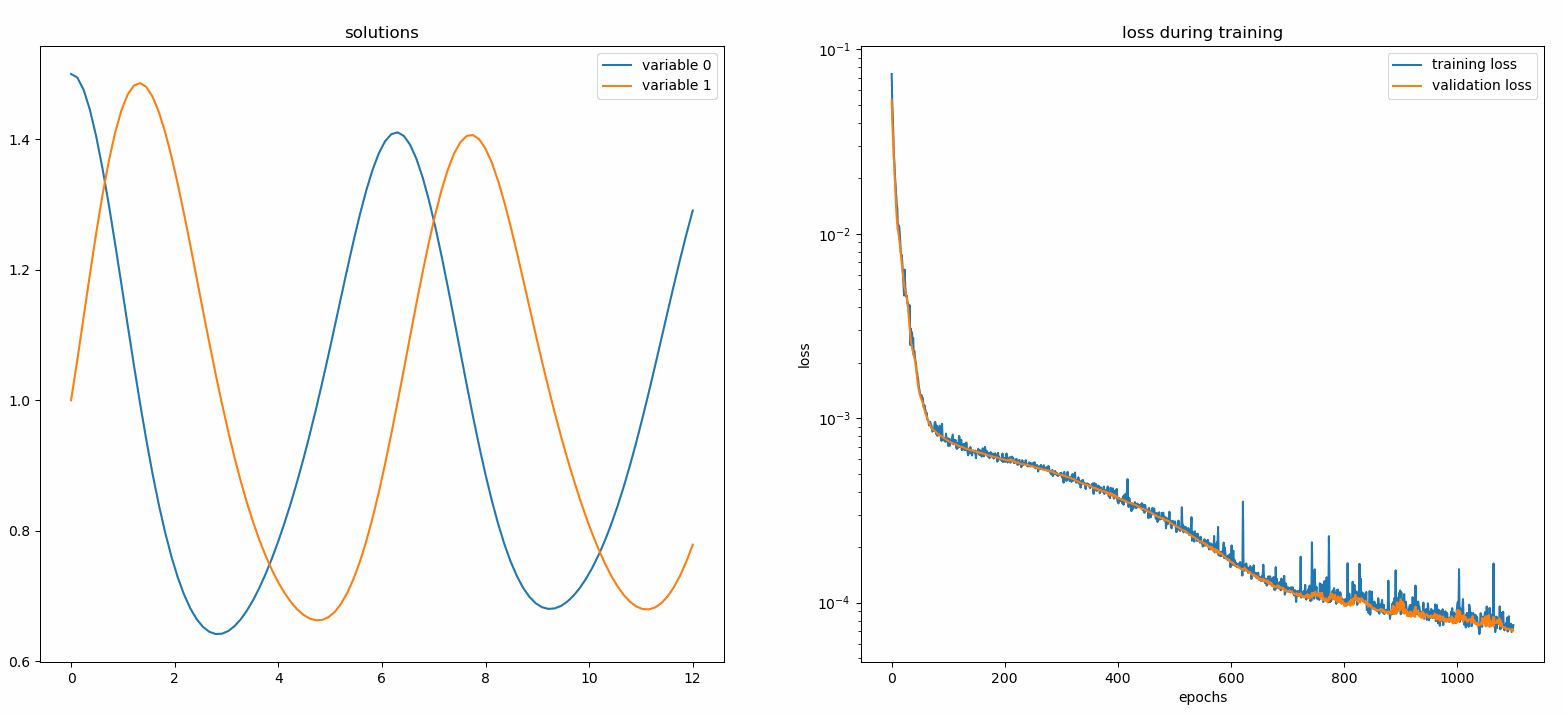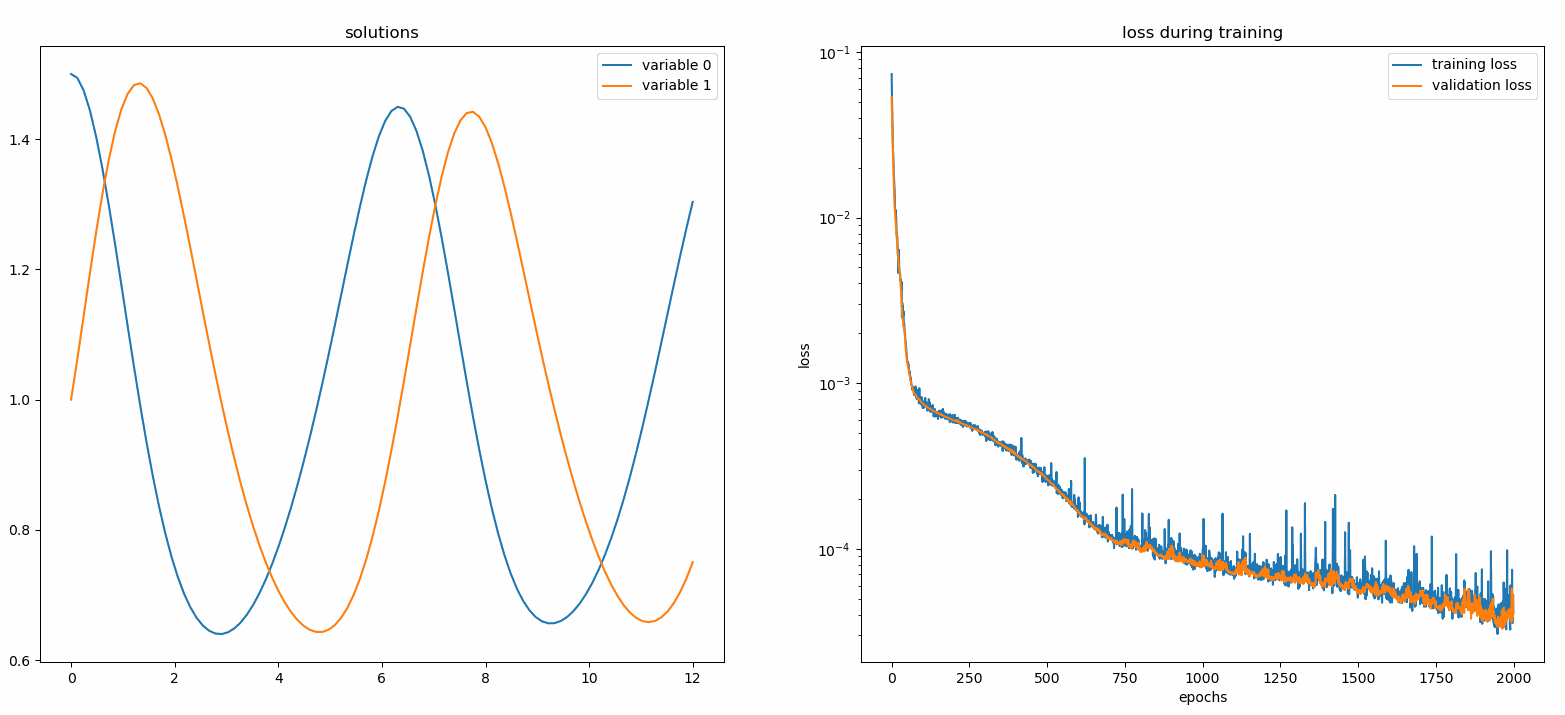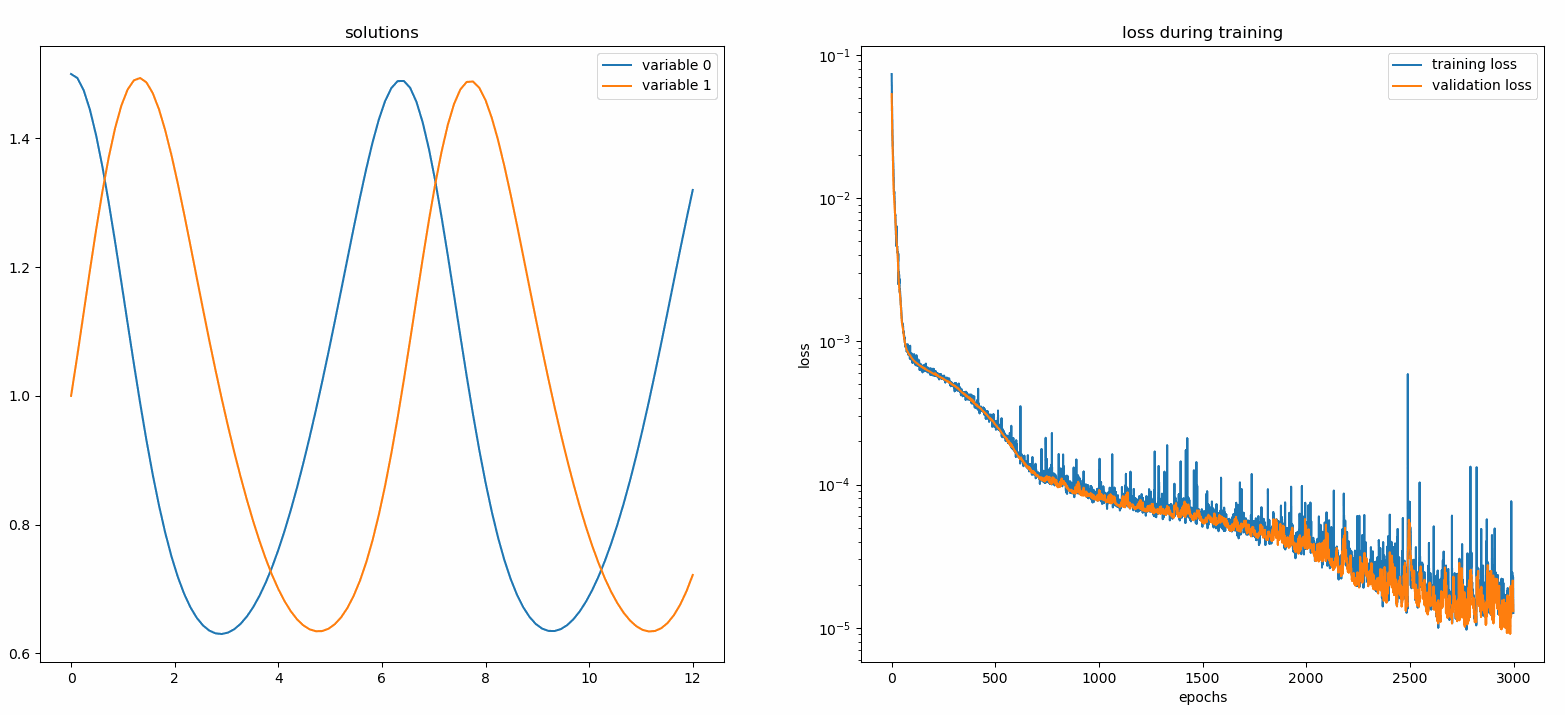
自定义网络

为了方便起见，我们实现了FCNN——全连接神经网络，其隐藏单元和激活函数可以自定义。

from neurodiffeq.networks import FCNN
# 默认: n_input_units=1, n_output_units=1, hidden_units=[32, 32], activation=torch.nn.Tanh
net1 = FCNN(n_input_units=..., n_output_units=..., hidden_units=[..., ..., ...], activation=...) 
...
nets = [net1, net2, ...]

FCNN通常是一个很好的起点。对于高级用户，求解器兼容任何自定义的torch.nn.Module。唯一的约束是：

1. 模块接受形状为(None, n_coords)的张量作为输入，并输出形状为(None, 1)的张量。

2. 传递给solver = Solver(..., nets=nets)的nets中必须总共有n_funcs个模块。

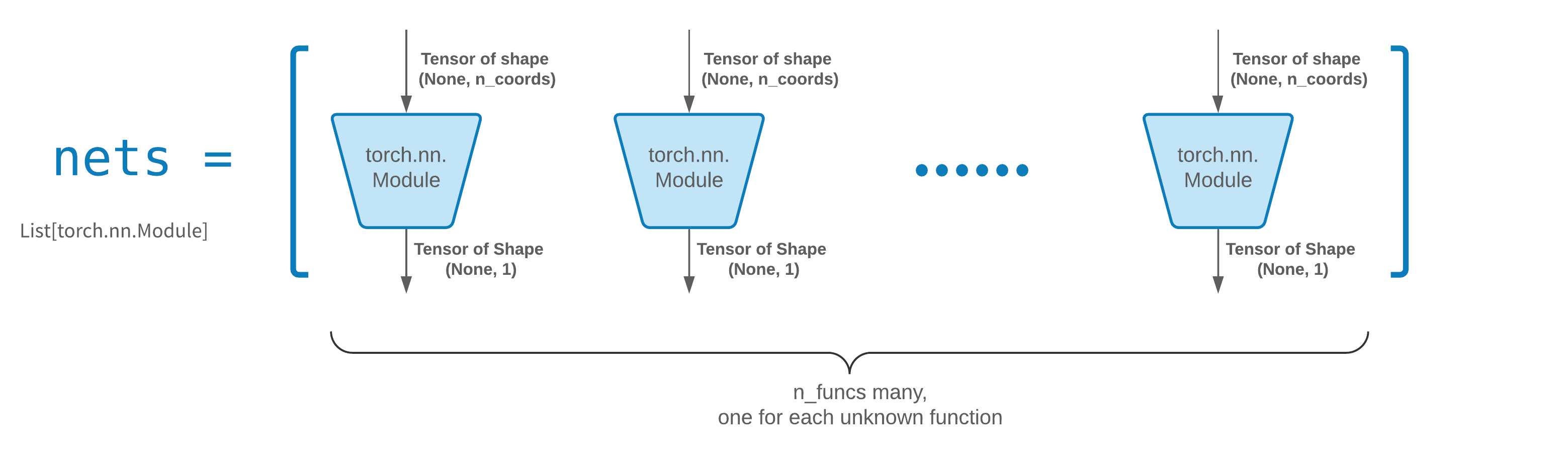
实际上，neurodiffeq有一个single_net功能，不遵循上述规则，这里不会涉及。

阅读PyTorch教程，了解如何构建自己的网络（即模块）架构。

迁移学习

通过将old_solver.nets（一个torch模块列表）序列化到磁盘，然后加载并传递给新的求解器，可以轻松实现迁移学习：

old_solver.fit(max_epochs=...)
# ... 将old_solver.nets保存到磁盘

# ... 从磁盘加载网络，存储在loaded_nets变量中
new_solver = Solver(..., nets=loaded_nets)
new_solver.fit(max_epochs=...)

我们目前正在开发用于保存/加载网络和Solver的其他内部变量的包装函数。同时，您可以阅读PyTorch教程，了解如何保存和加载网络。

采样策略

在neurodiffeq中，通过最小化在域内一组点上评估的损失（ODE/PDE残差）来训练网络。这些点每次都会随机重新采样。要控制采样点的数量、分布和边界域，您可以指定自己的训练/验证生成器。

from neurodiffeq.generators import Generator1D

# 默认 t_min=0.0, t_max=1.0, method='uniform', noise_std=None
g1 = Generator1D(size=..., t_min=..., t_max=..., method=..., noise_std=...)
g2 = Generator1D(size=..., t_min=..., t_max=..., method=..., noise_std=...)

solver = Solver1D(..., train_generator=g1, valid_generator=g2)

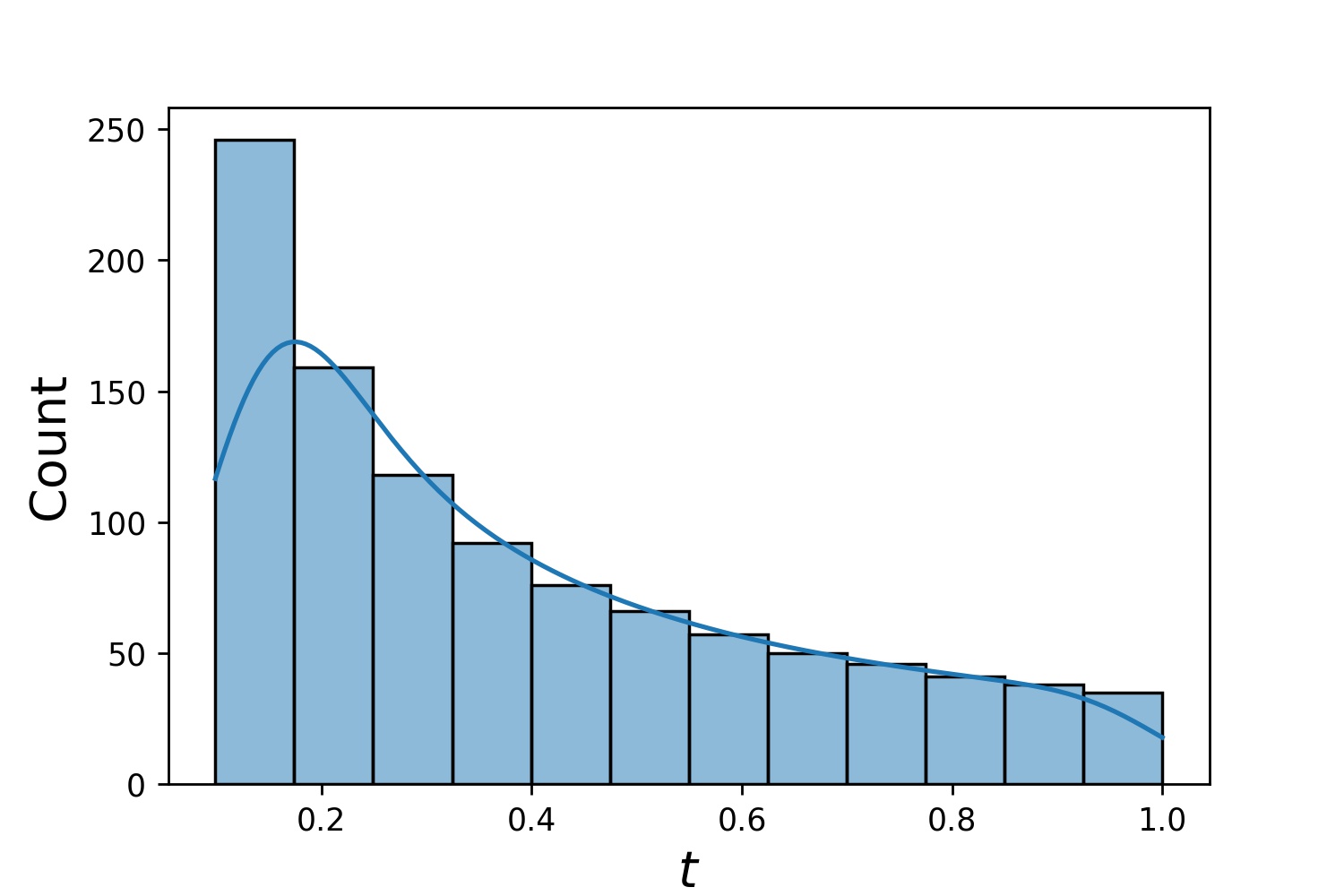
以下是Generator1D的一些样本分布。

Generator1D(8192, 0.0, 1.0, method='uniform')	Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3)

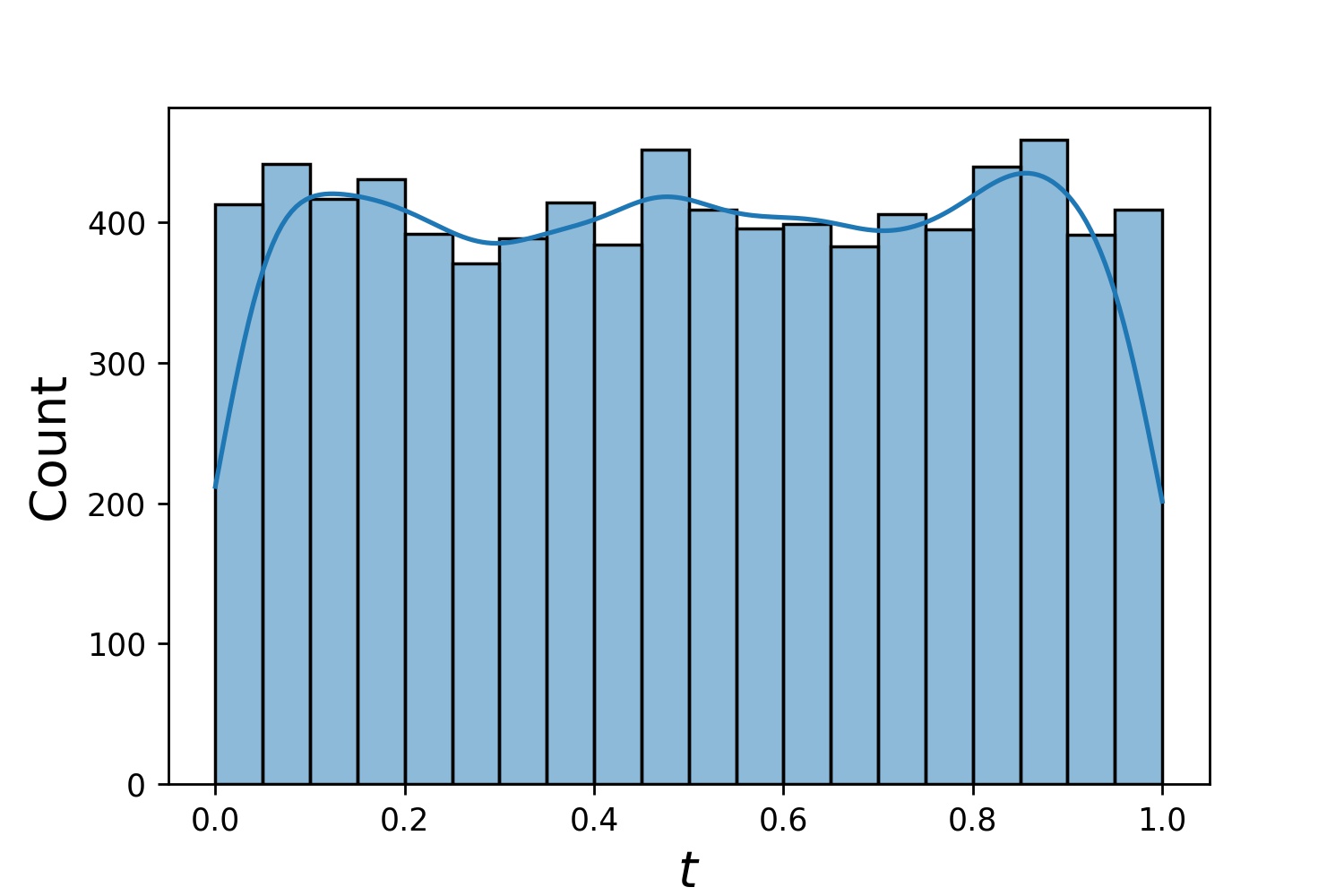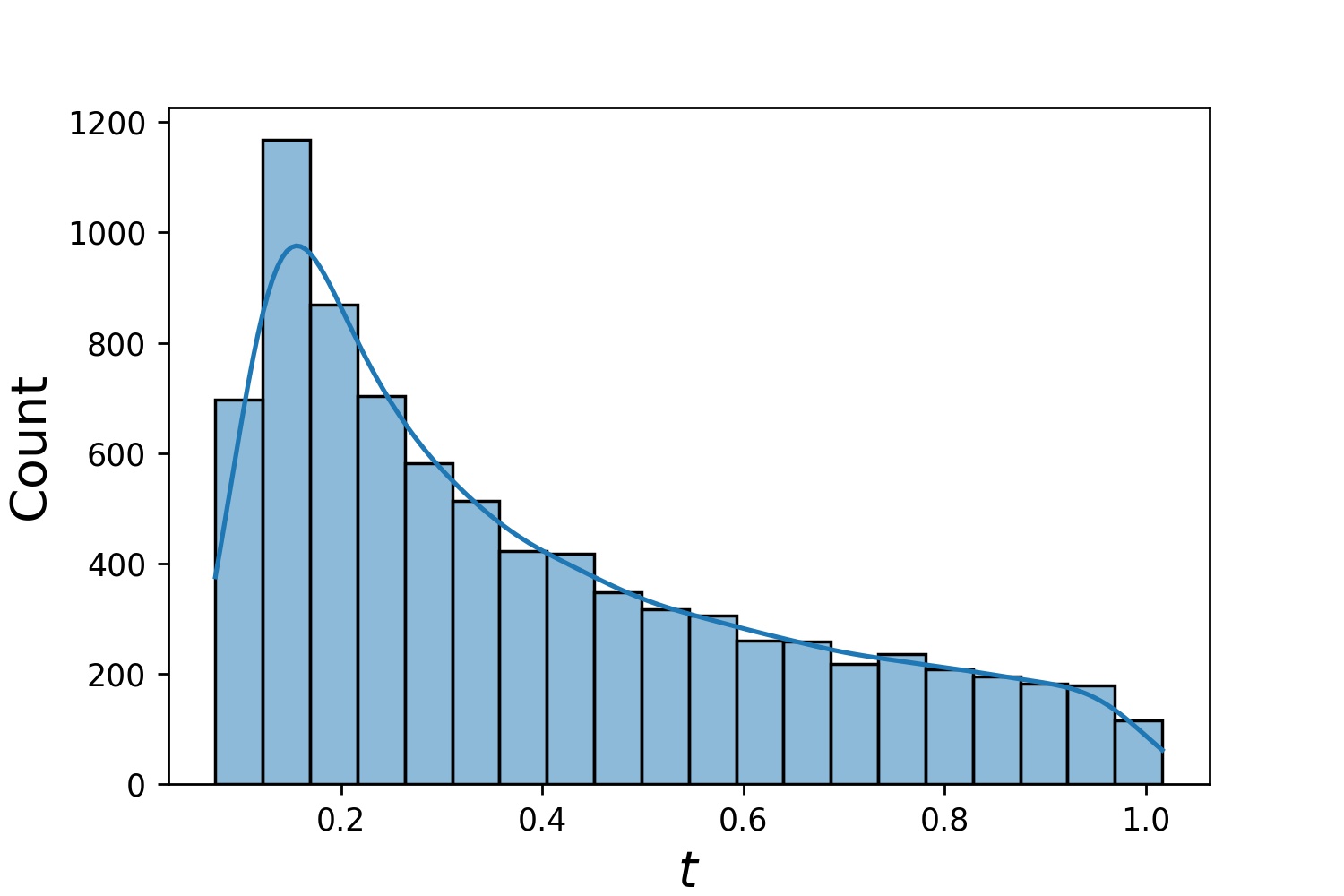注意，当同时指定train_generator和valid_generator时，可以在Solver1D(...)中省略t_min和t_max。事实上，即使您同时传递t_min、t_max、train_generator、valid_generator，t_min和t_max仍将被忽略。

组合生成器

生成器的另一个很好的特性是可以将它们连接在一起，例如

g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))
g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2))
g = g1 + g2

在这里，g将是一个输出g1和g2组合样本的生成器

g1	g2	g1 + g2

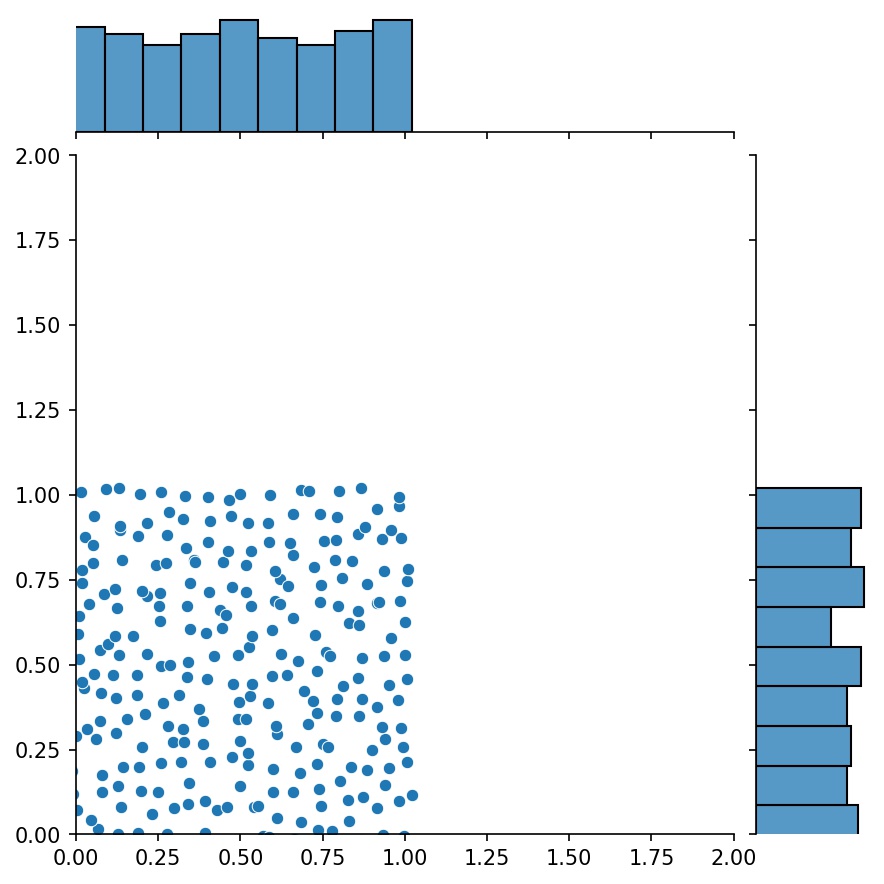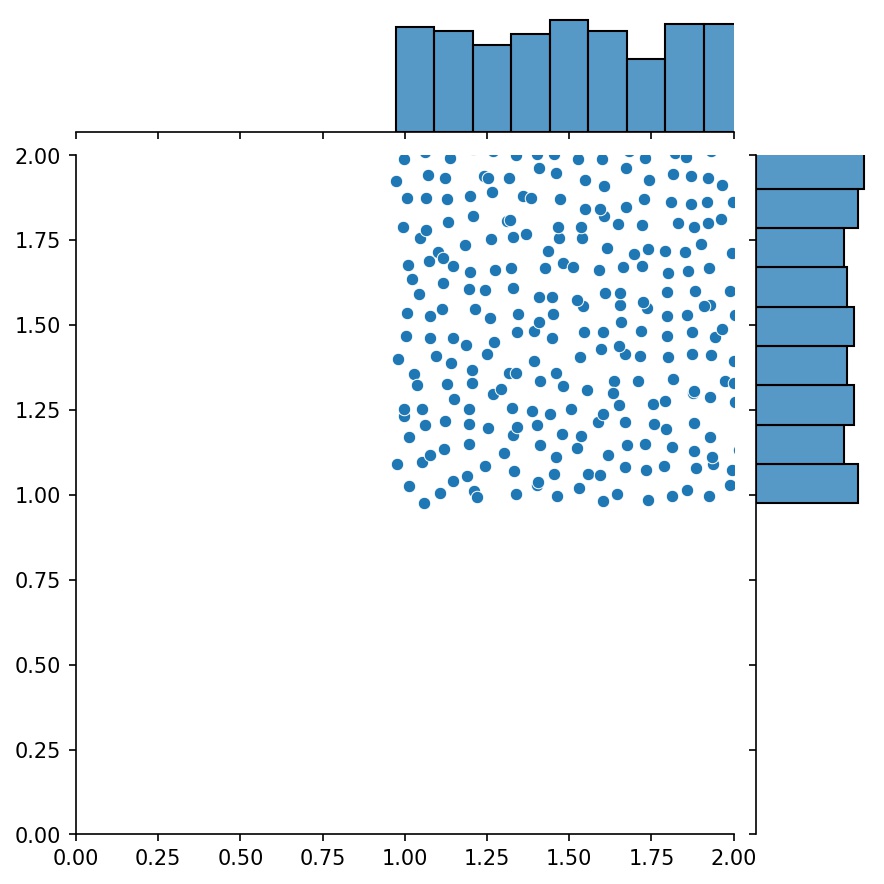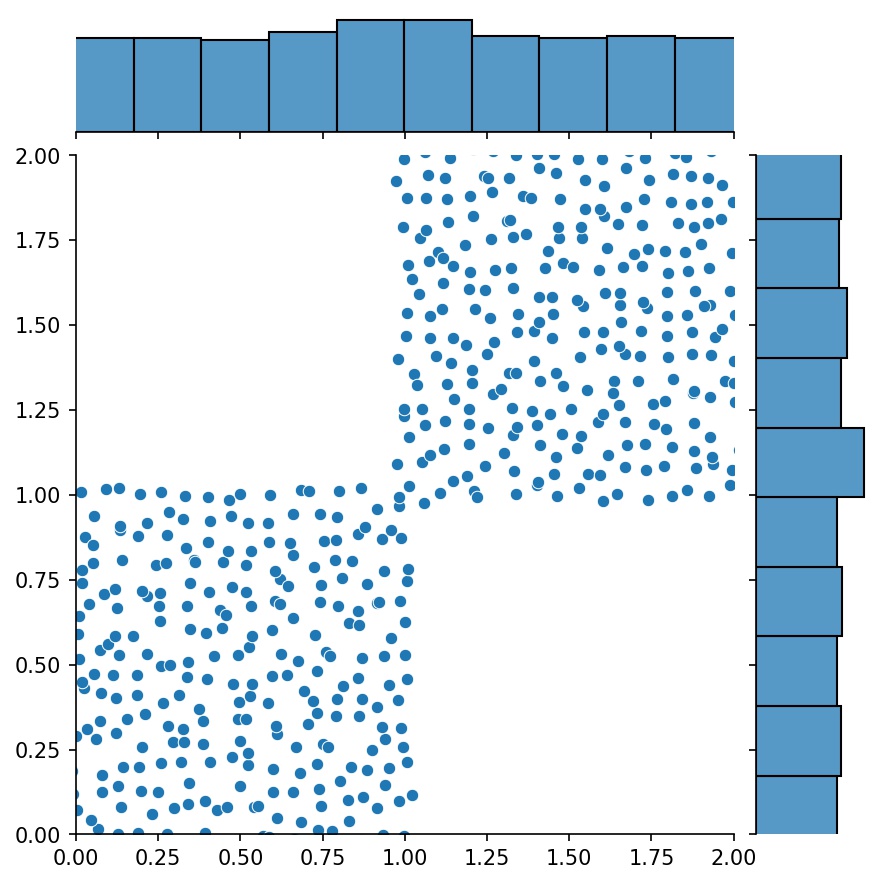采样高维空间

您可以使用Generator2D、Generator3D等来在高维空间中采样点。但还有另一种方法：

g1 = Generator1D(1024, 2.0, 3.0, method='uniform')
g2 = Generator1D(1024, 0.1, 1.0, method='log-spaced-noisy', noise_std=0.001)
g = g1 * g2

在这里，g将是一个生成器，每次产生1024个点，这些点位于二维矩形(2,3) × (0.1,1)中。这些点的x坐标从(2,3)区间内使用uniform策略抽取，y坐标从(0.1,1)区间内使用log-spaced-noisy策略抽取。

g1	g2	g1 * g2

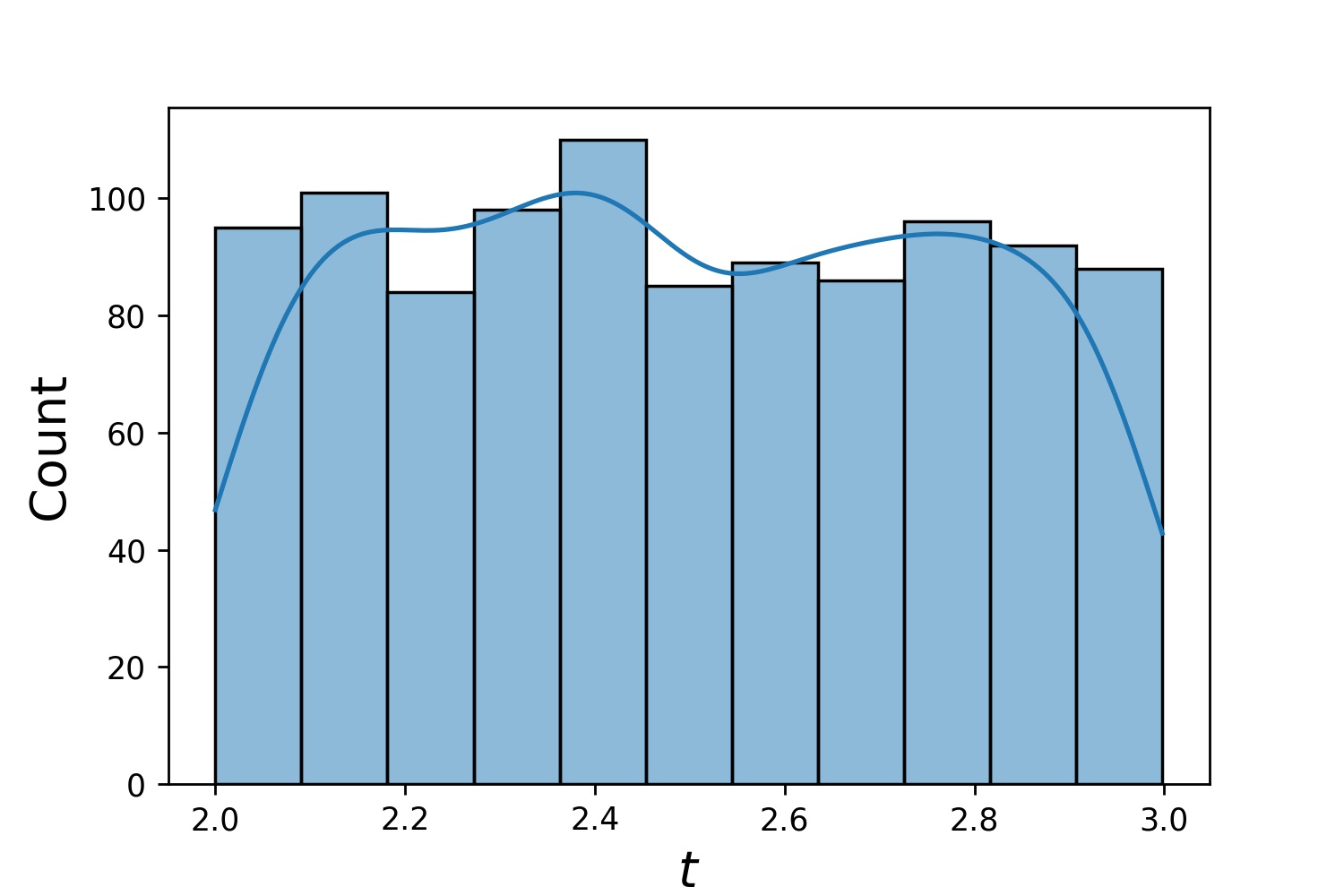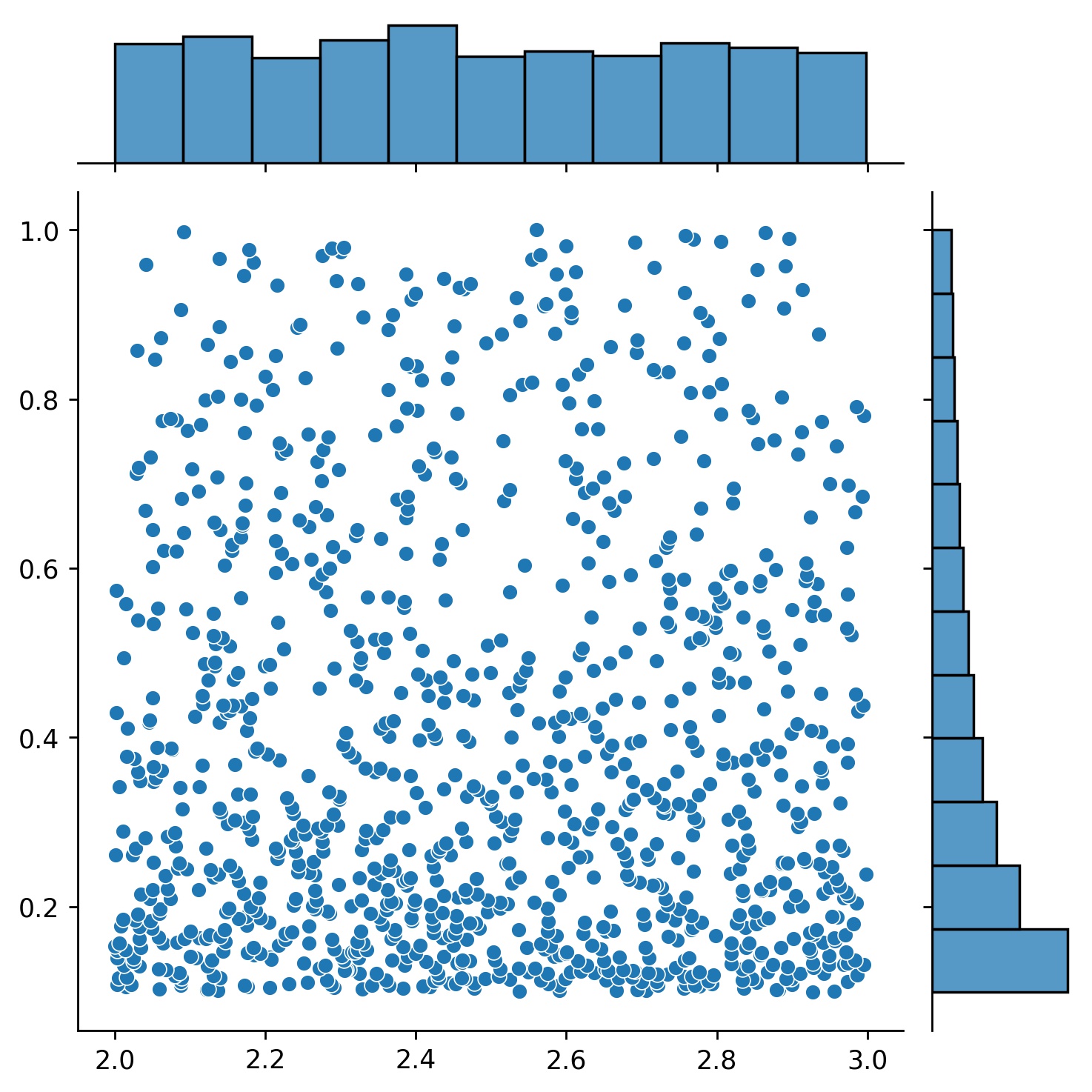解集和反问题

有时，一次性求解一组方程是很有意思的。例如，你可能想要求解形如du/dt + λu = 0的微分方程，其中初始条件为u(0) = U0。你可能想要一次性求解所有λ和U0的情况，通过将它们作为神经网络的输入来处理。

这种应用的一个例子是化学反应，其中反应速率是未知的。不同的反应速率对应不同的解，而只有一个解与观察到的数据点匹配。你可能对首先求解一组解，然后确定最佳反应速率（即方程参数）感兴趣。第二步被称为反问题。

以下是使用neurodiffeq来实现这一目标的示例：

1. 假设我们有一个方程du/dt + λu = 0和初始条件u(0) = U0，其中λ和U0是未知常数。我们还有一组观察值t_obs和u_obs。我们首先导入BundleSolver和BundleIVP，这对于获得解集是必要的：

   from neurodiffeq.conditions import BundleIVP
   from neurodiffeq.solvers import BundleSolver1D
   
   import matplotlib.pyplot as plt
   import numpy as np
   import torch
   from neurodiffeq import diff
   

2. 我们确定输入t的范围，以及参数λ和U0的范围。我们还需要决定参数的顺序。即哪个应该是第一个参数，哪个应该是第二个。为了演示的目的，我们选择λ作为第一个参数（索引0），U0作为第二个（索引1）。记住参数的索引非常重要。

   T_MIN, T_MAX = 0, 1
   LAMBDA_MIN, LAMBDA_MAX = 3, 5  # 第一个参数，索引 = 0
   U0_MIN, U0_MAX = 0.2, 0.6       # 第二个参数，索引 = 1
   

3. 然后我们像往常一样定义conditions和solver，只是我们使用BundleIVP和BundleSolver1D而不是IVP和Solver1D。这两者的接口与IVP和Solver1D非常相似。你可以在API参考中了解更多。

   # 方程参数跟在输入（通常是时间和空间坐标）之后
   diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]
   
   # BundleIVP中的关键字参数必须命名为"u_0"。如果你使用其他名称，如`y0`、`u0`等，将无法工作。
   conditions = [
       BundleIVP(t_0=0, u_0=None, bundle_param_lookup={'u_0': 1})  # u_0的索引为1
   ]
   
   solver = BundleSolver1D(
       ode_system=diff_eq,
       conditions=conditions,
       t_min=T_MIN, t_max=T_MAX, 
       theta_min=[LAMBDA_MIN, U0_MIN],  # λ的索引为0；u_0的索引为1
       theta_max=[LAMBDA_MAX, U0_MAX],  # λ的索引为0；u_0的索引为1
       eq_param_index=(0,),             # λ是唯一的方程参数，其索引为0
       n_batches_valid=1,
   )
   

   由于**λ是方程中的参数**，而**U0是初始条件中的参数**，我们必须在diff_eq中包含λ，在条件中包含U0。如果一个参数同时出现在方程和条件中，它必须同时包含在两个地方。传递给BundleSovler1D的conditions中的所有元素必须是Bundle*条件，即使它们没有参数。

4. 现在，我们可以像往常一样训练它并获得解决方案。

   solver.fit(max_epochs=1000)
   solution = solver.get_solution(best=True)
   

   该解决方案需要三个输入 - t、λ和U0。所有输入必须具有相同的形状。例如，如果你想固定λ=4和U0=0.4，并绘制t ∈ [0,1]范围内的解u，你可以这样做：

   t = np.linspace(0, 1)
   lmd = 4 * np.ones_like(t)
   u0 = 0.4 * np.ones_like(t)
   
   u = solution(t, lmd, u0, to_numpy=True)
   
   import matplotlib.pyplot as plt
   plt.plot(t, u)
   

5. 一旦你有了打包好的solution，你可以找到一组参数(λ, U0)，使其最接近观测到的数据点(t_i, u_i)。这可以通过简单的梯度下降来实现。在下面的示例中，我们假设只有三个数据点u(0.2) = 0.273、u(0.5)=0.129和u(0.8) = 0.0609。以下是经典的PyTorch工作流程。

   # 观测到的数据点
   t_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)
   u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)
   
   # λ和U0的随机初始化；跟踪它们的梯度
   lmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MIN
   u0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MIN
   adam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(True)], lr=1e-2)
   
   # 运行10000轮梯度下降
   for _ in range(10000):
       output = solution(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs))
       loss = ((output - u_obs) ** 2).mean()
       loss.backward()
       adam.step()
       adam.zero_grad()
      
   print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, loss = {loss.item()}")
   

常见问题

问：如何使用GPU进行训练？

很简单。在导入neurodiffeq时，库会自动检测你的机器上是否有可用的CUDA。由于该库基于PyTorch，如果找到兼容的GPU设备，它会将默认张量类型设置为torch.cuda.DoubleTensor。

问：如何使用预训练网络？

请参考自定义网络和迁移学习部分。

问：如何更改学习率？

使用标准的PyTorch方法。

1. 按照自定义网络中的说明构建你的网络：nets = [FCNN(), FCN(), ...]

2. 实例化一个自定义优化器，并将这些网络的所有参数传递给它

   parameters = [p for net in nets for p in net.parameters()]  # 所有网络的参数列表
   MY_LEARNING_RATE = 5e-3
   optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
   

3. 将你的nets和optimizer都传递给求解器：solver = Solver1D(..., nets=nets, optimizer=optimizer)

问：我得到了一个不好的解决方案。

与传统的数值方法（FEM、FVM等）不同，基于神经网络的解决方案需要一些超参数调整。该库提供了最大的灵活性来尝试任何超参数组合。

• 要使用不同的网络架构，你可以传入自定义的torch.nn.Module。
• 要使用不同的优化器，你可以将自己的优化器传递给solver = Solver(..., optimizer=my_optim)。
• 要使用不同的采样分布，你可以使用内置生成器或从头编写自己的生成器。
• 要使用不同的采样大小，你可以调整生成器或更改solver = Solver(..., n_batches_train)。
• 要在训练过程中动态更改超参数，请查看我们的回调功能。

问：有什么经验法则吗？

• 不要使用ReLU作为激活函数，因为它的二阶导数恒等于0。
• 将你的PDE/ODE重新缩放为无量纲形式，最好使所有内容都在[0,1]范围内。使用像[0,1000000]这样的域容易失败，因为a) PyTorch初始化模块权重相对较小，以及b) 大多数激活函数（如Sigmoid、Tanh、Swish）在0附近最不线性。
• 如果你的PDE/ODE太复杂，考虑尝试课程学习。开始在较小的域上训练你的网络，然后逐渐扩展直到覆盖整个域。

贡献

欢迎每个人为这个项目做出贡献。

在为这个仓库做出贡献时，我们考虑以下过程：

1. 打开一个issue来讨论你计划做出的更改。
2. 阅读贡献指南。
3. 在fork的仓库上进行更改，如果对接口做了更改，请更新README.md。
4. 打开一个拉取请求。