JavaScript 算法与数据结构

🇺🇦 乌克兰正遭受俄罗斯军队的攻击。平民正在被杀害。居民区正在遭受轰炸。

通过以下方式帮助乌克兰：

Serhiy Prytula 慈善基金会

Come Back Alive 慈善基金会

乌克兰国家银行

更多信息请访问 war.ukraine.ua 和乌克兰外交部

repo size

本仓库包含了多种基于 JavaScript 的算法与数据结构的示例。

每种算法和数据结构都有自己的 README，其中包含相关说明和进一步阅读的链接（包括YouTube视频链接）。

其他语言版本： 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Türkçe, Italiana, Bahasa Indonesia, Українська, Arabic, Tiếng Việt, Deutsch, Uzbek

☝ 请注意，这个项目仅用于学习和研究目的，不适用于生产环境。

数据结构

数据结构是一种在计算机中组织和存储数据的特定方式，使其能够高效地被访问和修改。更确切地说，数据结构是数据值的集合，它们之间的关系，以及可以应用于数据的函数或操作。

请记住，每种数据结构都有其自身的权衡。你需要更多地关注为什么选择某种数据结构，而不是如何实现它。

B - 初级, A - 高级

B 链表
B 双向链表
B 队列
B 栈
B 哈希表
B 堆 - 最大堆和最小堆
B 优先队列
A 字典树
A 树
- A 二叉搜索树
- A AVL 树
- A 红黑树
- A 线段树 - 包含最小/最大/总和范围查询示例
- A 树状数组 (二进制索引树)
A 图 (有向图和无向图)
A 并查集 - 一种联合-查找数据结构
A 布隆过滤器
A LRU 缓存 - 最近最少使用（LRU）缓存

算法

算法是解决一类问题的明确规范。它是一系列精确定义操作序列的规则集。

B - 初级, A - 高级

按主题分类的算法

数学
- B 位运算 - 设置/获取/更新/清除位，乘/除以二，取负数等
- B 二进制浮点数 - 浮点数的二进制表示
- B 阶乘
- B 斐波那契数 - 经典和闭式版本
- B 质因数 - 寻找质因数并使用Hardy-Ramanujan定理计数
- B 素数测试 (试除法)
- B 欧几里得算法 - 计算最大公约数（GCD）
- B 最小公倍数 (LCM)
- B 埃拉托斯特尼筛法 - 找出给定限制内的所有质数
- B 判断2的幂 - 检查数字是否为2的幂（朴素和位运算算法）
- B 杨辉三角
- B 复数 - 复数及其基本运算
- B 弧度和角度 - 弧度与角度的互相转换
- B 快速幂
- B 霍纳法则 - 多项式求值
- B 矩阵 - 矩阵及基本矩阵运算（乘法、转置等）
- B 欧几里得距离 - 点/向量/矩阵之间的距离
- A 整数拆分
- A 平方根 - 牛顿法
- A 刘徽割圆术 - 基于N边形的π近似计算
- A 离散傅里叶变换 - 将时间函数（信号）分解为构成它的频率
集合
- B 笛卡尔积 - 多个集合的乘积
- B Fisher–Yates 洗牌算法 - 有限序列的随机排列
- A 幂集 - 集合的所有子集（位运算、回溯和级联解法）
- A 排列 (有重复和无重复)
- A 组合 (有重复和无重复)
- A 最长公共子序列 (LCS)
- A 最长递增子序列
- A 最短公共超序列 (SCS)
- A 背包问题 - "0/1"和"无界"两种情况
- A 最大子数组 - "暴力法"和"动态规划"（Kadane算法）
- A 组合求和 - 找出形成特定和的所有组合
字符串
- B 汉明距离 - 符号不同的位置数
- B 回文串 - 检查字符串是否为回文
- A 莱温斯坦距离 - 两个序列之间的最小编辑距离
- A KMP算法 - 子串搜索（模式匹配）
- A Z算法 - 子串搜索（模式匹配）
- A Rabin Karp算法 - 子串搜索
- A 最长公共子串
- A 正则表达式匹配
搜索
- B 线性搜索
- B 跳转搜索（或块搜索）- 在排序数组中搜索
- B 二分查找 - 在排序数组中搜索
- B 插值搜索 - 在均匀分布的排序数组中搜索
排序
- B 冒泡排序
- B 选择排序
- B 插入排序
- B 堆排序
- B 归并排序
- B 快速排序 - 原地和非原地实现
- B 希尔排序
- B 计数排序
- B 基数排序
- B 桶排序
链表
- B 正向遍历
- B 反向遍历
树
- B 深度优先搜索 (DFS)
- B 广度优先搜索 (BFS)
图
- B 深度优先搜索 (DFS)
- B 广度优先搜索 (BFS)
- B 克鲁斯卡尔算法 - 寻找加权无向图的最小生成树 (MST)
- A 戴克斯特拉算法 - 找到单个顶点到所有图顶点的最短路径
- A 贝尔曼-福特算法 - 找到单个顶点到所有图顶点的最短路径
- A 弗洛伊德-沃沙尔算法 - 找到所有顶点对之间的最短路径
- A 检测环 - 对有向图和无向图（基于DFS和不相交集的版本）
- A 普里姆算法 - 寻找加权无向图的最小生成树 (MST)
- A 拓扑排序 - DFS 方法
- A 关节点 - Tarjan算法（基于DFS）
- A 桥 - 基于DFS的算法
A 欧拉路径和欧拉回路 - Fleury算法 - 每条边恰好访问一次
A 哈密顿回路 - 每个顶点恰好访问一次
A 强连通分量 - Kosaraju算法
A 旅行商问题 - 访问每个城市并返回起点城市的最短可能路线
密码学
- B 多项式哈希 - 基于多项式的滚动哈希函数
- B 栅栏密码 - 用于编码消息的换位密码算法
- B 凯撒密码 - 简单的替换密码
- B 希尔密码 - 基于线性代数的替换密码
机器学习
- B 纳米神经元 - 7个简单的JS函数，展示机器如何实际学习（前向/反向传播）
- B k-NN - k近邻分类算法
- B k均值 - k均值聚类算法
图像处理
- B 接缝裁剪 - 内容感知图像缩放算法
统计学
- B 加权随机 - 基于项目权重从列表中选择随机项
进化算法
- A 遗传算法 - 展示如何将遗传算法应用于训练自动泊车汽车的示例
未分类
- B 汉诺塔
- B 方阵旋转 - 原地算法
- B 跳跃游戏 - 回溯、动态规划（自顶向下+自底向上）和贪心示例
- B 不同路径 - 回溯、动态规划和基于帕斯卡三角形的示例
- B 雨水收集 - 接雨水问题（动态规划和暴力版本）
- B 递归楼梯 - 计算达到顶部的方法数（4种解法）
- B 买卖股票的最佳时机 - 分治和一次遍历示例
- A N皇后问题
- A 骑士巡游

按范式分类的算法

算法范式是一种通用方法或方法，是一类算法设计的基础。它是比算法更高层的抽象，就像算法是比计算机程序更高层的抽象一样。

暴力法 - 查看所有可能性并选择最佳解决方案
- B 线性搜索
- B 雨水收集 - 接雨水问题
- B 递归楼梯 - 计算达到顶部的方法数
- A 最大子数组
- A 旅行商问题 - 访问每个城市并返回原点的最短可能路线
- A 离散傅里叶变换 - 将时间函数（信号）分解为构成它的频率
贪心 - 在当前时间选择最佳选项，不考虑未来
- B 跳跃游戏
- A 无界背包问题
- A 迪杰斯特拉算法 - 找到所有图顶点的最短路径
- A 普里姆算法 - 寻找加权无向图的最小生成树 (MST)
- A 克鲁斯卡尔算法 - 寻找加权无向图的最小生成树 (MST)
分治法 - 将问题分解成更小的部分，然后解决这些部分
- B 二分查找
- B 汉诺塔
- B 杨辉三角
- B 欧几里得算法 - 计算最大公约数 (GCD)
- B 归并排序
- B 快速排序
- B 树深度优先搜索 (DFS)
- B 图深度优先搜索 (DFS)
- B 矩阵 - 生成和遍历不同形状的矩阵
- B 跳跃游戏
- B 快速幂
- B 最佳买卖股票时机 - 分治和一次遍历示例
- A 排列 (有重复和无重复)
- A 组合 (有重复和无重复)
- A 最大子数组
动态规划 - 使用先前找到的子解构建解决方案
- B 斐波那契数
- B 跳跃游戏
- B 不同路径
- B 雨水收集 - 接雨水问题
- B 递归楼梯 - 计算达到顶部的方法数
- B 接缝裁剪 - 内容感知图像缩放算法
- A 莱文斯坦距离 - 两个序列之间的最小编辑距离
- A 最长公共子序列 (LCS)
- A 最长公共子串
- A 最长递增子序列
- A 最短公共超序列
- A 0/1背包问题
- A 整数拆分
- A 最大子数组
- A 贝尔曼-福特算法 - 寻找所有图顶点的最短路径
- A 弗洛伊德算法 - 找到所有顶点对之间的最短路径
- A 正则表达式匹配
回溯法 - 类似于暴力法，尝试产生所有可能的解决方案，但每次生成下一个解决方案时测试如果它满足所有条件，只有在这种情况下才继续生成后续解决方案。否则，回溯，并继续寻找不同的解决方案路径。通常使用DFS遍历状态空间。
- B 跳跃游戏
- B 不同路径
- B 幂集 - 一个集合的所有子集
- A 哈密顿回路 - 恰好访问每个顶点一次
- A N皇后问题
- A 骑士巡逻
- A 组合总和 - 找出形成特定总和的所有组合
分支限界法 - 记住在回溯搜索的每个阶段找到的最低成本解决方案，并使用到目前为止找到的最低成本解决方案的成本作为下限，以丢弃成本大于最低成本解决方案的部分解决方案。通常，使用BFS遍历与DFS遍历状态空间树的组合。

如何使用此仓库

安装所有依赖

npm install

运行ESLint

你可能想运行它来检查代码质量。

npm run lint

运行所有测试

npm test

按名称运行测试

npm test -- 'LinkedList'

故障排除

如果lint或测试失败，尝试删除node_modules文件夹并重新安装npm包：

rm -rf ./node_modules
npm i

同时确保你使用的是正确的Node版本（>=16）。如果你使用nvm进行Node版本管理，你可以从项目的根文件夹运行nvm use，正确的版本将被选择。

游乐场

你可以在./src/playground/playground.js文件中使用数据结构和算法，并在./src/playground/__test__/playground.test.js中为其编写测试。

然后只需运行以下命令来测试你的游乐场代码是否按预期工作：

npm test -- 'playground'

有用信息

参考

大O表示法

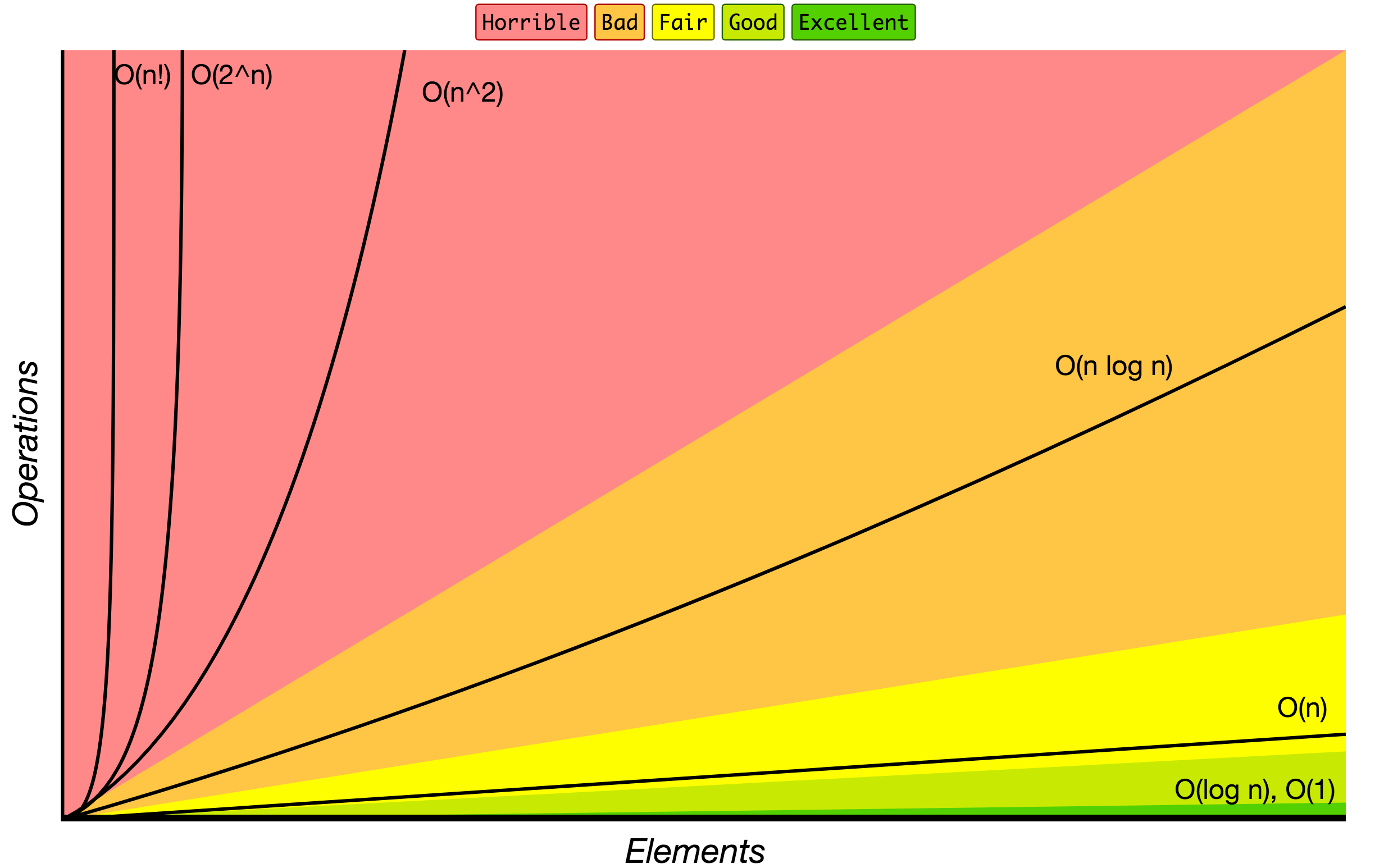
大O表示法用于根据输入大小的增长来分类算法的运行时间或空间需求如何增长。在下面的图表中，你可以找到最常见的算法增长阶数，用大O表示法指定。大O复杂度图表

来源：Big O 速查表。

以下是一些最常用的大O表示法及其在不同输入数据规模下的性能比较。

大O表示法	类型	10个元素的计算次数	100个元素的计算次数	1000个元素的计算次数
O(1)	常数	1	1	1
O(log N)	对数	3	6	9
O(N)	线性	10	100	1000
O(N log N)	线性对数	30	600	9000
O(N^2)	平方	100	10000	1000000
O(2^N)	指数	1024	1.26e+29	1.07e+301
O(N!)	阶乘	3628800	9.3e+157	4.02e+2567

数据结构操作复杂度

数据结构	访问	搜索	插入	删除	备注
数组	1	n	n	n
栈	n	n	1	1
队列	n	n	1	1
链表	n	n	1	n
哈希表	-	n	n	n	在完美哈希函数的情况下，复杂度为O(1)
二叉搜索树	n	n	n	n	在平衡树的情况下，复杂度为O(log(n))
B树	log(n)	log(n)	log(n)	log(n)
红黑树	log(n)	log(n)	log(n)	log(n)
AVL树	log(n)	log(n)	log(n)	log(n)
布隆过滤器	-	1	1	-	搜索时可能出现假阳性

数组排序算法复杂度

名称	最佳情况	平均情况	最坏情况	内存	稳定性	备注
冒泡排序	n	n²	n²	1	是
插入排序	n	n²	n²	1	是
选择排序	n²	n²	n²	1	否
堆排序	n log(n)	n log(n)	n log(n)	1	否
归并排序	n log(n)	n log(n)	n log(n)	n	是
快速排序	n log(n)	n log(n)	n²	log(n)	否	快速排序通常使用原地排序，栈空间为O(log(n))
希尔排序	n log(n)	取决于间隔序列	n (log(n))²	1	否
计数排序	n + r	n + r	n + r	n + r	是	r - 数组中的最大数
基数排序	n * k	n * k	n * k	n + k	是	k - 最长键的长度