k-means-constrained:带有最小和最大聚类大小约束的K-means聚类算法
K-means聚类是一种广泛使用的无监督学习算法,用于将数据点划分为K个簇。然而,传统的K-means算法不允许用户控制每个簇的大小,这在某些应用场景中可能会导致不理想的结果。为了解决这个问题,k-means-constrained算法应运而生。
k-means-constrained是一种改进的K-means聚类实现,它允许用户为每个聚类指定最小和最大大小约束。这种方法在保持K-means高效性的同时,提供了更灵活的聚类控制。
算法原理
k-means-constrained的核心思想是修改K-means算法的聚类分配步骤。具体来说,它将聚类分配问题转化为最小成本流(Minimum Cost Flow, MCF)线性网络优化问题。这个优化问题通过成本缩放推送重标记(cost-scaling push-relabel)算法求解,该算法使用了Google的Operations Research工具中的SimpleMinCostFlow实现,这是一个高效的C++实现。
这种方法的灵感来自Bradley等人的研究。k-means-constrained对原始的MCF网络进行了修改,使其不仅可以指定最小聚类大小,还可以指定最大聚类大小。
主要特点
-
大小约束: 允许用户为每个聚类指定最小和最大大小。
-
基于scikit-learn: 代码基于scikit-learn的
KMeans实现,保持了相似的API,便于用户使用。 -
高效实现: 利用Google的Operations Research工具实现最小成本流算法,保证了计算效率。
-
灵活性: 可以根据具体应用需求调整聚类大小约束。
安装
k-means-constrained可以通过pip轻松安装:
pip install k-means-constrained
该库支持Python 3.8及以上版本。
使用示例
以下是一个简单的使用示例:
from k_means_constrained import KMeansConstrained
import numpy as np
# 准备数据
X = np.array([[1, 2], [1, 4], [1, 0],
[4, 2], [4, 4], [4, 0]])
# 初始化KMeansConstrained
clf = KMeansConstrained(
n_clusters=2,
size_min=2,
size_max=5,
random_state=0
)
# 拟合数据并预测
labels = clf.fit_predict(X)
print("聚类标签:", labels)
# 获取聚类中心
print("聚类中心:\n", clf.cluster_centers_)
在这个例子中,我们指定了2个聚类,每个聚类的最小大小为2,最大大小为5。
时间复杂度和运行时间
k-means-constrained算法比传统的K-means算法更复杂,因此执行时间更长,扩展性也较差。假设数据点数量为n,聚类数量为c,则时间复杂度如下:
- K-means: O(nc)
- k-means-constrained: O((n³c+n²c²+nc³)log(n+c))
这里假设算法迭代次数和数据点特征维度是常数。当n和c同阶时:
- K-means: O(n²)
- k-means-constrained: O(n⁴log(n))
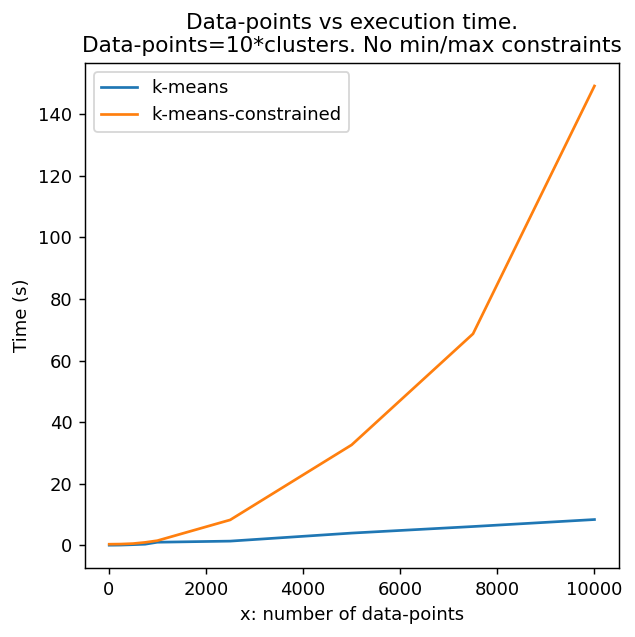
上图展示了K-means和k-means-constrained的运行时间对比。可以看出,随着数据点和聚类数量的增加,k-means-constrained的运行时间增长更快。
应用场景
k-means-constrained在许多实际应用中非常有用,例如:
-
电子组件装配: 在表面贴装技术(SMT)中,需要将电子元件分组,每组的元件数量不能超过给定的上限。
-
数据库挖掘: 在并行挖掘关联规则时,为了保证良好的并行性,需要控制每个分区的项集数量大致相同。
-
客户分群: 在市场细分中,可能需要控制每个细分市场的客户数量在一定范围内。
-
图像分割: 在某些图像处理任务中,可能需要控制每个分割区域的像素数量。
-
资源分配: 在资源分配问题中,可能需要确保每个组分配到的资源数量在一定范围内。
局限性
尽管k-means-constrained提供了更灵活的聚类控制,但它也有一些局限性:
-
计算复杂度: 相比传统K-means,k-means-constrained的计算复杂度更高,尤其是在处理大规模数据时。
-
初始化敏感: 与K-means类似,k-means-constrained的结果也可能受到初始化的影响。
-
约束可能导致次优解: 添加大小约束可能会导致算法收敛到局部最优解,而不是全局最优解。
-
不适用于高维数据: 在高维空间中,欧氏距离可能失去意义,影响聚类效果。
未来发展方向
-
算法优化: 进一步优化算法,提高大规模数据处理能力。
-
支持更多距离度量: 除欧氏距离外,添加对其他距离度量的支持。
-
并行化: 实现并行版本,以更好地利用多核处理器。
-
自适应约束: 开发自动调整聚类大小约束的方法。
-
与其他算法集成: 探索与其他聚类或降维技术的结合。
结论
k-means-constrained为传统K-means算法添加了大小约束,提供了更灵活的聚类控制。虽然计算复杂度较高,但在许多实际应用中,这种灵活性是非常有价值的。随着算法的不断优化和应用范围的扩大,k-means-constrained有望在数据科学和机器学习领域发挥更重要的作用。
对于那些需要精确控制聚类大小的应用场景,k-means-constrained无疑是一个强大而有用的工具。然而,使用者需要权衡其带来的灵活性和增加的计算成本,根据具体问题选择最适合的聚类方法。









