Documentation

k-means-constrained

K-means clustering implementation whereby a minimum and/or maximum size for each cluster can be specified.

This K-means implementation modifies the cluster assignment step (E in EM) by formulating it as a Minimum Cost Flow (MCF) linear network optimisation problem. This is then solved using a cost-scaling push-relabel algorithm and uses Google's Operations Research tools's SimpleMinCostFlow which is a fast C++ implementation.

This package is inspired by Bradley et al.. The original Minimum Cost Flow (MCF) network proposed by Bradley et al. has been modified so maximum cluster sizes can also be specified along with minimum cluster size.

The code is based on scikit-lean's KMeans and implements the same API with modifications.

Ref:

1. Bradley, P. S., K. P. Bennett, and Ayhan Demiriz. "Constrained k-means clustering." Microsoft Research, Redmond (2000): 1-8.
2. Google's SimpleMinCostFlow C++ implementation

Installation

You can install the k-means-constrained from PyPI:

pip install k-means-constrained

It is supported on Python 3.8 and above.

Example

More details can be found in the API documentation.

>>> from k_means_constrained import KMeansConstrained
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
...                [4, 2], [4, 4], [4, 0]])
>>> clf = KMeansConstrained(
...     n_clusters=2,
...     size_min=2,
...     size_max=5,
...     random_state=0
... )
>>> clf.fit_predict(X)
array([0, 0, 0, 1, 1, 1], dtype=int32)
>>> clf.cluster_centers_
array([[ 1.,  2.],
       [ 4.,  2.]])
>>> clf.labels_
array([0, 0, 0, 1, 1, 1], dtype=int32)

<details> <summary>Code only</summary>

from k_means_constrained import KMeansConstrained
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],
                [4, 2], [4, 4], [4, 0]])
clf = KMeansConstrained(
     n_clusters=2,
     size_min=2,
     size_max=5,
     random_state=0
 )
clf.fit_predict(X)
clf.cluster_centers_
clf.labels_

</details>

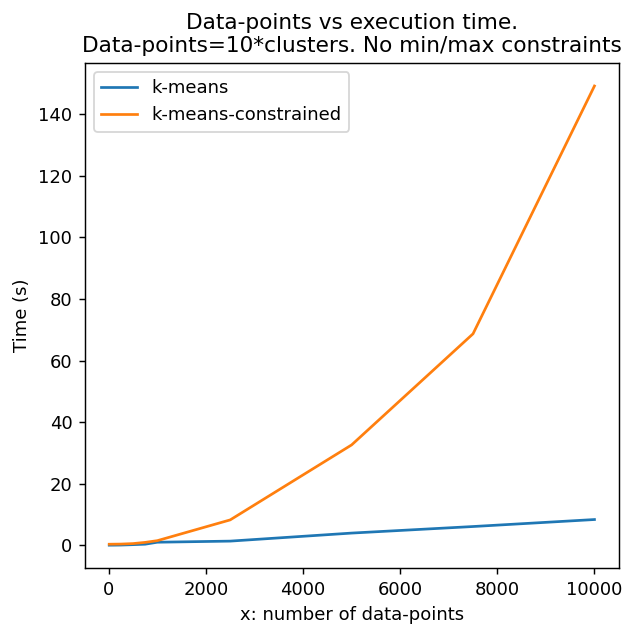
Time complexity and runtime

k-means-constrained is a more complex algorithm than vanilla k-means and therefore will take longer to execute and has worse scaling characteristics.

Given a number of data points $n$ and clusters $c$, the time complexity of:

• k-means: $\mathcal{O}(nc)$
• k-means-constrained¹: $\mathcal{O}((n^3c+n^2c^2+nc^3)\log(n+c)))$

This assumes a constant number of algorithm iterations and data-point features/dimensions.

If you consider the case where $n$ is the same order as $c$ ($n \backsim c$) then:

• k-means: $\mathcal{O}(n^2)$
• k-means-constrained¹: $\mathcal{O}(n^4\log(n)))$

Below is a runtime comparison between k-means and k-means-constrained whereby the number of iterations, initializations, multi-process pool size and dimension size are fixed. The number of clusters is also always one-tenth the number of data points $n=10c$. It is shown above that the runtime is independent of the minimum or maximum cluster size, and so none is included below.

<p align="center"> <img src="https://raw.githubusercontent.com/joshlk/k-means-constrained/master/etc/execution_time.png" alt="Data-points vs execution time for k-means vs k-means-constrained. Data-points=10*clusters. No min/max constraints" width="50%" height="50%"> </p> <details> <summary>System details</summary>

• OS: Linux-5.15.0-75-generic-x86_64-with-glibc2.35
• CPU: AMD EPYC 7763 64-Core Processor
• CPU cores: 120
• k-means-constrained version: 0.7.3
• numpy version: 1.24.2
• scipy version: 1.11.1
• ortools version: 9.6.2534
• joblib version: 1.3.1
• sklearn version: 1.3.0

</details> ---

¹: Ortools states the time complexity of their cost-scaling push-relabel algorithm for the min-cost flow problem as $\mathcal{O}(n^2m\log(nC))$ where $n$ is the number of nodes, $m$ is the number of edges and $C$ is the maximum absolute edge cost.

Citations

If you use this software in your research, please use the following citation:

@software{Levy-Kramer_k-means-constrained_2018,
author = {Levy-Kramer, Josh},
month = apr,
title = {{k-means-constrained}},
url = {https://github.com/joshlk/k-means-constrained},
year = {2018}
}