LoRA和DoRA:从零开始实现低秩适应技术

在深度学习领域,如何高效地微调大型预训练模型一直是一个热门话题。近年来,低秩适应(Low-Rank Adaptation, LoRA)技术因其出色的参数效率和微调性能而备受关注。最近,研究人员又提出了DoRA(Weight-Decomposed Low-Rank Adaptation)技术,进一步改进了LoRA的性能。本文将深入探讨LoRA和DoRA这两种先进的模型微调方法,并提供从零开始的PyTorch实现代码,帮助读者全面理解这些技术的原理和应用。

LoRA技术简介

LoRA是一种用于高效微调大型预训练模型的技术,特别适用于大型语言模型(LLM)和视觉Transformer等模型。其核心思想是:在微调过程中,不直接更新原始的大型权重矩阵,而是学习一个低秩的更新矩阵。这种方法大大减少了需要更新的参数数量,从而降低了计算成本和内存需求。

具体来说,LoRA的工作原理如下:

对于原始的权重矩阵W,LoRA引入两个小的矩阵A和B。
更新后的权重矩阵表示为:W' = W + AB
矩阵A和B的维度远小于W,因此参数量大大减少。

例如,如果W是一个1000x1000的矩阵,传统微调需要更新100万个参数。而使用LoRA,如果选择秩为2,那么A是1000x2的矩阵,B是2x1000的矩阵,总共只需要更新4000个参数,减少了250倍。

LoRA的PyTorch实现

下面我们来看看如何用PyTorch从零实现LoRA层:

import torch.nn as nn

class LoRALayer(nn.Module):
    def __init__(self, in_dim, out_dim, rank, alpha):
        super().__init__()
        std_dev = 1 / torch.sqrt(torch.tensor(rank).float())
        self.A = nn.Parameter(torch.randn(in_dim, rank) * std_dev)
        self.B = nn.Parameter(torch.zeros(rank, out_dim))
        self.alpha = alpha

    def forward(self, x):
        x = self.alpha * (x @ self.A @ self.B)
        return x

class LinearWithLoRA(nn.Module):
    def __init__(self, linear, rank, alpha):
        super().__init__()
        self.linear = linear
        self.lora = LoRALayer(
            linear.in_features, linear.out_features, rank, alpha
        )

    def forward(self, x):
        return self.linear(x) + self.lora(x)

这里的LoRALayer实现了LoRA的核心功能,而LinearWithLoRA则将LoRA应用到现有的线性层上。

DoRA:LoRA的进阶版本

DoRA(Weight-Decomposed Low-Rank Adaptation)是对LoRA的一种改进。DoRA的核心思想是将预训练权重矩阵分解为幅度向量和方向矩阵,然后仅对方向矩阵应用LoRA更新,同时单独训练幅度向量。

DoRA的工作流程如下:

将预训练权重矩阵W分解为幅度向量m和方向矩阵V。
对方向矩阵V应用LoRA更新。
在训练过程中同时更新幅度向量m。

DoRA的优势在于:

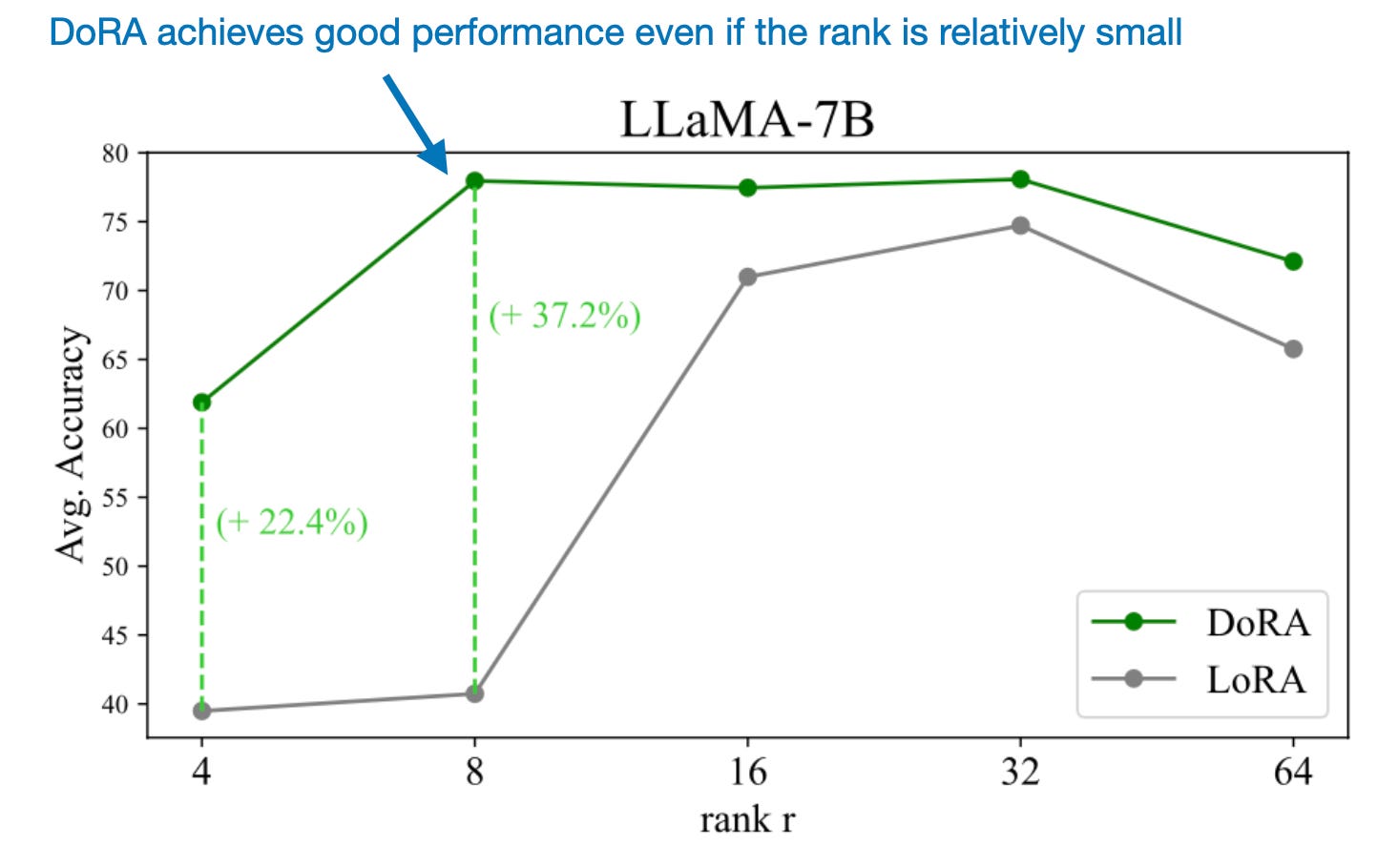
性能提升:在多项基准测试中,DoRA的表现优于LoRA。
参数效率:即使DoRA的秩减半,其性能仍然可以超过LoRA。
对秩参数不敏感:DoRA对秩的选择更加鲁棒,减少了超参数调优的工作量。

DoRA性能对比图

DoRA的PyTorch实现

下面是DoRA的PyTorch实现代码:

class LinearWithDoRAMerged(nn.Module):
    def __init__(self, linear, rank, alpha):
        super().__init__()
        self.linear = linear
        self.lora = LoRALayer(
            linear.in_features, linear.out_features, rank, alpha
        )
        self.m = nn.Parameter(
            self.linear.weight.norm(p=2, dim=0, keepdim=True))

    def forward(self, x):
        lora = self.lora.A @ self.lora.B
        numerator = self.linear.weight + self.lora.alpha*lora.T
        denominator = numerator.norm(p=2, dim=0, keepdim=True)
        directional_component = numerator / denominator
        new_weight = self.m * directional_component
        return F.linear(x, new_weight, self.linear.bias)

这个实现中,我们首先计算LoRA更新,然后将其应用到原始权重上。接着,我们对更新后的权重进行归一化,得到方向矩阵。最后,我们将方向矩阵与可学习的幅度向量相乘,得到最终的权重矩阵。

实际应用

在实际应用中,我们可以轻松地将现有神经网络中的线性层替换为DoRA层:

model.layers[0] = LinearWithDoRAMerged(model.layers[0], rank=4, alpha=8)
model.layers[2] = LinearWithDoRAMerged(model.layers[2], rank=4, alpha=8)
model.layers[4] = LinearWithDoRAMerged(model.layers[4], rank=4, alpha=8)

然后,我们可以冻结原始线性层的权重,只训练DoRA层的参数:

def freeze_linear_layers(model):
    for child in model.children():
        if isinstance(child, nn.Linear):
            for param in child.parameters():
                param.requires_grad = False
        else:
            freeze_linear_layers(child)

freeze_linear_layers(model)