NeuroDiffEq: 基于神经网络求解微分方程的强大工具

NeuroDiffEq简介

NeuroDiffEq是一个开源的Python库,旨在利用人工神经网络求解微分方程。它基于PyTorch构建,为用户提供了一套灵活而强大的工具,可以轻松地解决各种复杂的常微分方程(ODE)和偏微分方程(PDE)问题。

微分方程是描述函数与其导数之间关系的方程,在科学和工程领域有着广泛的应用。传统上,这类问题通常通过数值方法(如有限差分法、有限元法等)来求解。尽管这些方法行之有效,但它们在函数表示上存在一定的局限性。而NeuroDiffEq则提供了一种新的思路 - 利用神经网络来逼近微分方程的解,从而得到连续可微的解析解。

作为通用函数逼近器,人工神经网络已被证明具有求解常微分方程和偏微分方程的潜力。NeuroDiffEq的目标就是将这些现有的技术实现为一个灵活的软件包,使其能够适用于广泛的用户定义问题。

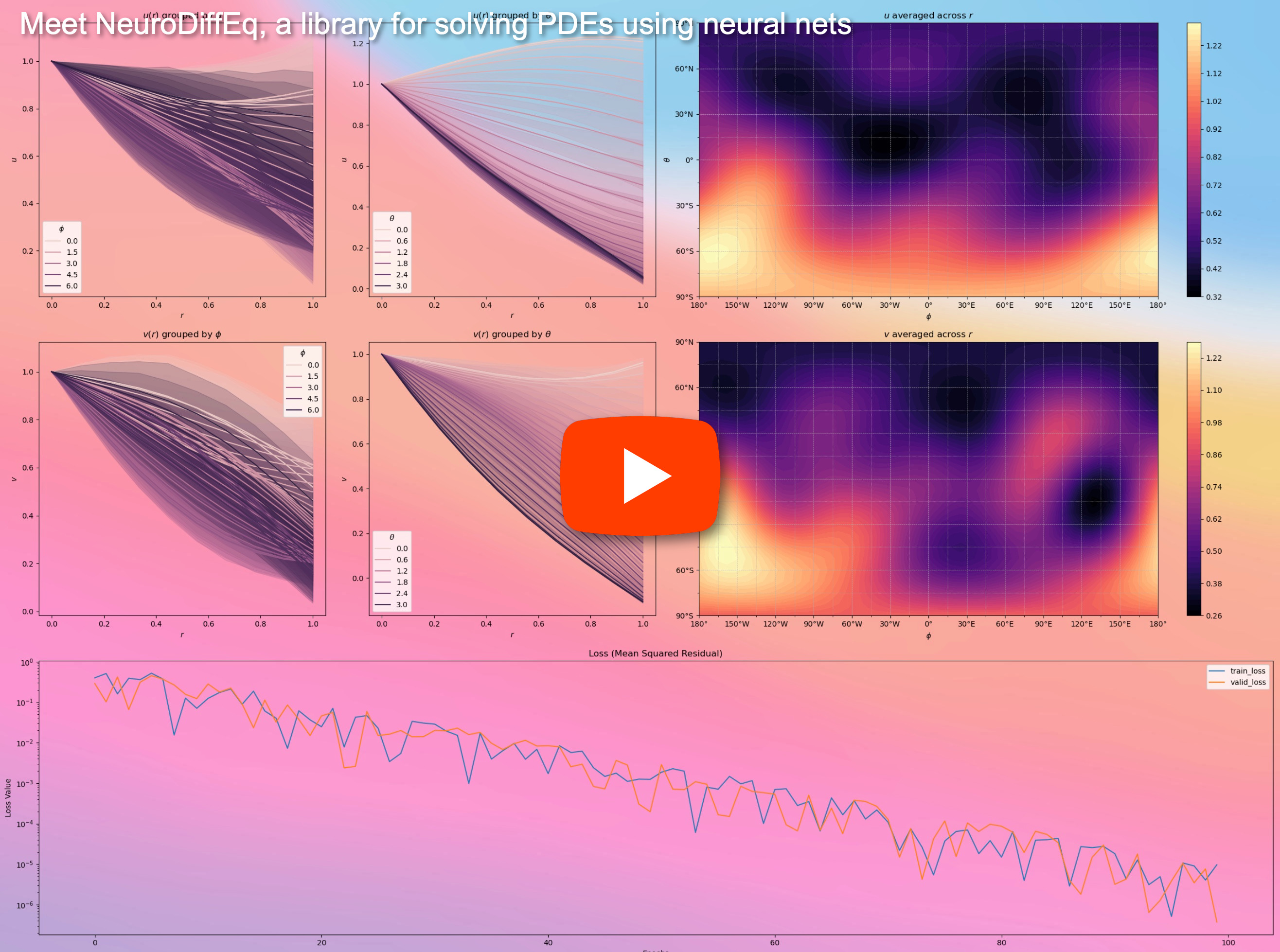
NeuroDiffEq的主要特性

NeuroDiffEq具有以下几个主要特性:

1. 基于神经网络的求解: 利用神经网络的强大拟合能力来逼近微分方程的解。

2. 支持多种方程类型: 可以求解常微分方程(ODE)和偏微分方程(PDE),包括初值问题和边值问题。

3. 灵活的网络架构: 用户可以自定义神经网络结构,以适应不同的问题复杂度。

4. 多种采样策略: 提供多种采样方法来生成训练数据点,以提高求解精度。

5. 可视化监控: 内置监控工具,可以实时查看求解过程和结果。

6. 支持GPU加速: 自动检测并利用GPU资源进行加速计算。

7. 支持迁移学习: 可以利用预训练模型来加速新问题的求解。

安装和使用

NeuroDiffEq可以通过pip轻松安装:

pip install -U neurodiffeq

对于想要获取最新开发版本的用户,也可以通过GitHub直接安装:

git clone https://github.com/NeuroDiffGym/neurodiffeq.git
cd neurodiffeq && pip install -r requirements
pip install .

使用示例

下面我们通过两个简单的例子来展示NeuroDiffEq的基本用法。

求解ODE系统

首先,我们来看一个非线性ODE系统的例子 - 著名的Lotka–Volterra方程(捕食者-猎物模型):

from neurodiffeq import diff
from neurodiffeq.solvers import Solver1D
from neurodiffeq.conditions import IVP
from neurodiffeq.networks import FCNN, SinActv

def ode_system(u, v, t): 
    return [diff(u,t)-(u-u*v), diff(v,t)-(u*v-v)]

conditions = [IVP(t_0=0.0, u_0=1.5), IVP(t_0=0.0, u_0=1.0)]
nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]

solver = Solver1D(ode_system, conditions, t_min=0.1, t_max=12.0, nets=nets)
solver.fit(max_epochs=3000)
solution = solver.get_solution()

这段代码定义了Lotka–Volterra方程系统,设置了初值条件,并使用NeuroDiffEq提供的求解器来求解。求解结果如下图所示:

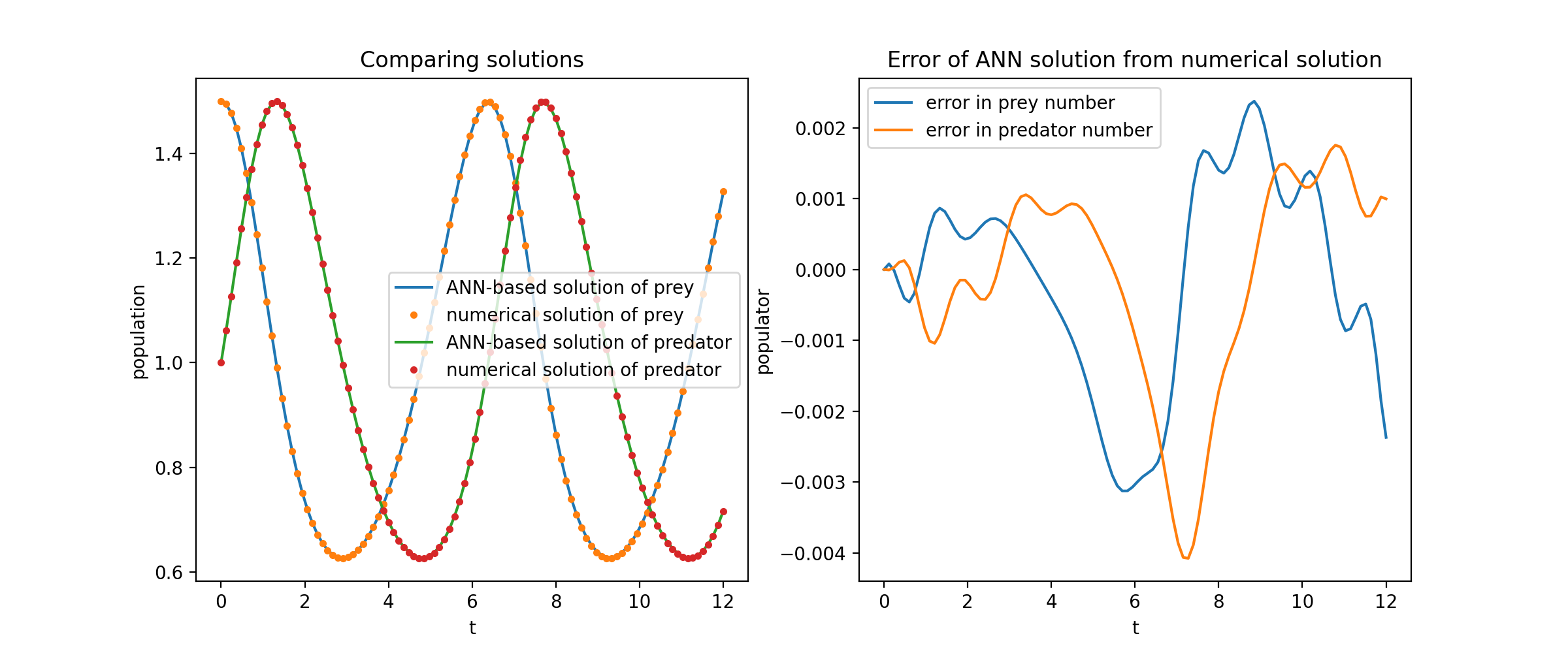
求解PDE系统

接下来,我们来看一个PDE的例子 - 求解具有Dirichlet边界条件的Laplace方程:

from neurodiffeq.solvers import Solver2D
from neurodiffeq.conditions import DirichletBVP2D

def pde_system(u, x, y):
    return [diff(u, x, order=2) + diff(u, y, order=2)]

conditions = [
    DirichletBVP2D(
        x_min=0, x_min_val=lambda y: torch.sin(np.pi*y),
        x_max=1, x_max_val=lambda y: 0,                   
        y_min=0, y_min_val=lambda x: 0,                   
        y_max=1, y_max_val=lambda x: 0,                   
    )
]
nets = [FCNN(n_input_units=2, n_output_units=1, hidden_units=(512,))]

solver = Solver2D(pde_system, conditions, xy_min=(0, 0), xy_max=(1, 1), nets=nets)
solver.fit(max_epochs=2000)
solution = solver.get_solution()

求解结果如下图所示:

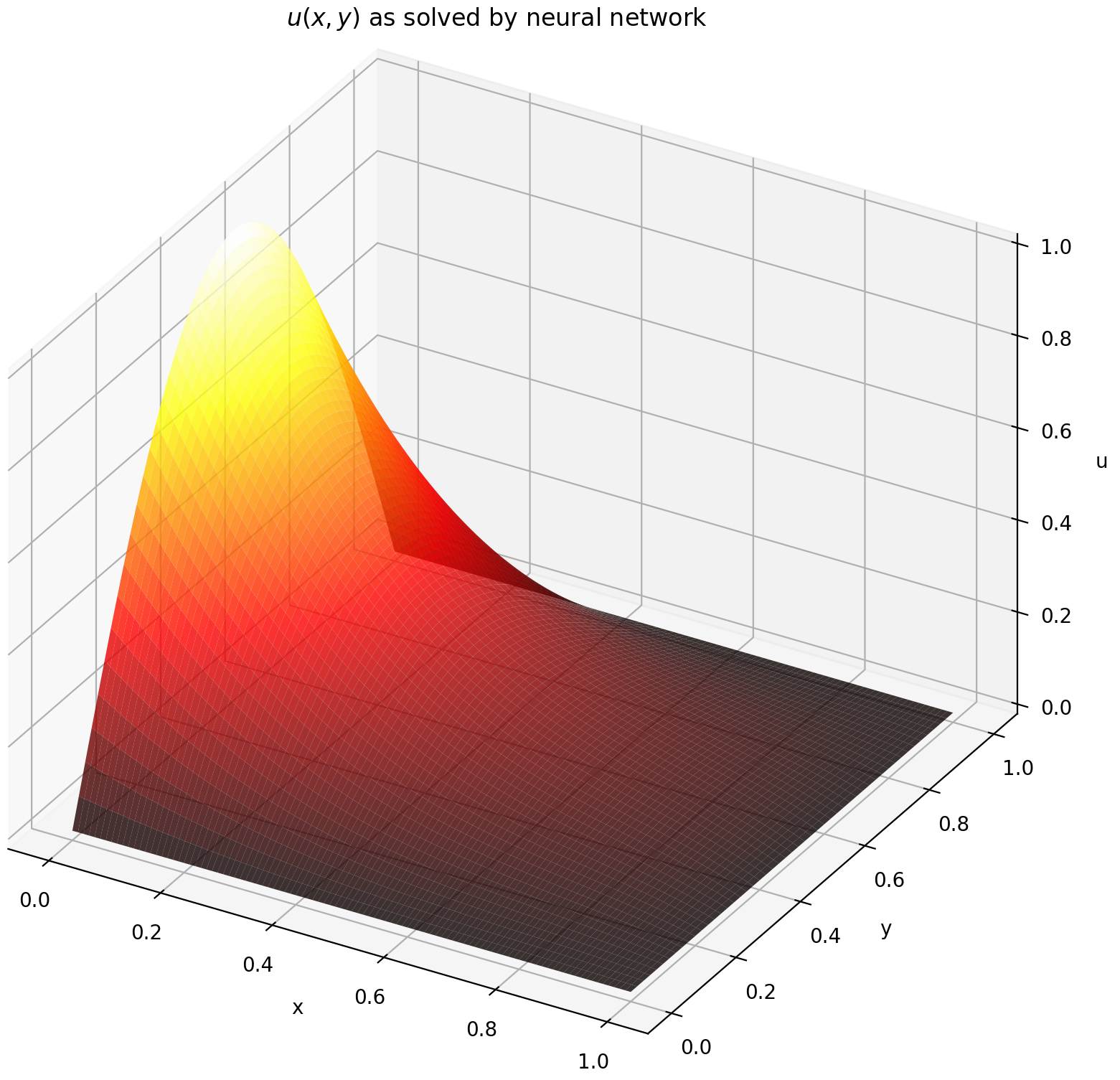
高级功能

除了基本的求解功能,NeuroDiffEq还提供了许多高级特性,使其能够应对更复杂的问题和场景。

自定义网络

NeuroDiffEq允许用户自定义神经网络结构。默认提供了全连接神经网络(FCNN),用户可以根据需要调整网络的层数、每层的神经元数量以及激活函数:

from neurodiffeq.networks import FCNN
net = FCNN(n_input_units=..., n_output_units=..., hidden_units=[..., ..., ...], activation=...)

对于更高级的用户,还可以使用任何自定义的PyTorch模块作为求解网络。

采样策略

NeuroDiffEq提供了多种采样策略,用于生成训练和验证数据点。用户可以通过自定义生成器来控制采样点的数量、分布和边界:

from neurodiffeq.generators import Generator1D

g1 = Generator1D(size=..., t_min=..., t_max=..., method=..., noise_std=...)
g2 = Generator1D(size=..., t_min=..., t_max=..., method=..., noise_std=...)

solver = Solver1D(..., train_generator=g1, valid_generator=g2)

监控和可视化

NeuroDiffEq提供了监控工具,可以实时查看求解过程中的损失变化和解的形态:

from neurodiffeq.monitors import Monitor1D

monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)
solver.fit(..., callbacks=[monitor.to_callback()])

解集束和反问题

NeuroDiffEq还支持求解方程族(解集束)和反问题。这在处理具有未知参数的方程时特别有用,例如化学反应速率未知的情况。用户可以先求解一族解,然后通过与观测数据比较来确定最佳参数。

总结

NeuroDiffEq为微分方程求解提供了一种新颖而强大的方法。它结合了神经网络的灵活性和传统数值方法的精确性,为科研工作者和工程师提供了一个强大的工具。无论是求解简单的ODE还是复杂的PDE系统,NeuroDiffEq都能够胜任。

随着深度学习技术的不断发展,基于神经网络的微分方程求解方法必将在未来发挥越来越重要的作用。NeuroDiffEq作为这一领域的先驱工具之一,值得所有对计算科学感兴趣的人深入探索和使用。

要了解更多关于NeuroDiffEq的信息,欢迎访问其GitHub仓库或官方文档。无论你是科研工作者、工程师还是学生,NeuroDiffEq都将为你的微分方程求解之旅带来新的可能性。