《统计学习方法》笔记:从原理到R语言实现

《统计学习方法》是李航教授所著的机器学习经典教材,深入浅出地介绍了统计学习的基本方法。本文将对该书的核心内容进行详细解读,并结合R语言代码实现,帮助读者更好地理解和掌握统计学习的理论与实践。

统计学习方法概述

统计学习方法是一类从数据中学习的方法,用于解决分类、回归、聚类等问题。其基本思路是:通过给定的训练数据集,学习出一个模型,再利用模型对新数据进行预测。

统计学习的三要素是:模型、策略和算法。模型是所要学习的条件概率分布或决策函数;策略是模型选择的准则,通常是损失函数或风险函数最小化;算法是学习模型的具体计算方法。

在模型选择时,需要注意过拟合与欠拟合的问题。过拟合是指模型在训练数据上表现很好,但在测试数据上表现较差;欠拟合则相反。解决这一问题的方法包括正则化、交叉验证等。

感知机

感知机是二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别。感知机学习旨在求得一个分离超平面,使得正实例和负实例分布在超平面的两侧。

感知机学习算法的原始形式是:

1. 选取初始值w0,b0
2. 在训练集中选取数据(xi,yi)
3. 如果yi(w·xi+b)≤0,则更新w和b: w <- w + ηyixi b <- b + ηyi
4. 重复步骤2和3直到没有误分类点

这里η是学习率。可以证明,当训练数据线性可分时,感知机学习算法的收敛性是有保证的(Novikoff定理)。

感知机算法的对偶形式将w和b表示为实例xi和yi的线性组合,可以更方便地计算内积。

# R语言实现感知机算法
perceptron <- function(X, y, max_iter = 1000, eta = 0.1) {
  n <- nrow(X)
  d <- ncol(X)
  w <- rep(0, d)
  b <- 0
  
  for (iter in 1:max_iter) {
    wrong <- 0
    for (i in 1:n) {
      if (y[i] * (sum(w * X[i,]) + b) <= 0) {
        w <- w + eta * y[i] * X[i,]
        b <- b + eta * y[i]
        wrong <- wrong + 1
      }
    }
    if (wrong == 0) break
  }
  
  return(list(w = w, b = b))
}

k近邻法

k近邻法(kNN)是一种基本分类与回归方法。kNN的基本做法是:对给定的测试实例,在训练集中找到与之最邻近的k个实例,然后基于这k个实例的主要类别来进行预测。

kNN算法的关键在于如何确定距离或相似度。常用的距离度量包括:

1. 欧氏距离
2. 曼哈顿距离
3. 闵可夫斯基距离
4. 马氏距离

为了提高kNN算法的效率,通常需要使用特殊的数据结构如kd树。kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。

# R语言实现kNN算法
library(class)

knn_predict <- function(train, test, train_labels, k) {
  predictions <- knn(train, test, train_labels, k)
  return(predictions)
}

朴素贝叶斯

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。朴素贝叶斯法的基本思路是:对于给定的输入x,通过学习先验概率分布P(Y=ck)和条件概率分布P(X=x|Y=ck),利用贝叶斯定理求出后验概率P(Y=ck|X=x),将后验概率最大的类作为x的类输出。

朴素贝叶斯法的关键假设是特征条件独立性,即:

P(X=x|Y=ck) = P(X1=x1|Y=ck) * P(X2=x2|Y=ck) * ... * P(Xn=xn|Y=ck)

朴素贝叶斯法的学习与分类算法可概括为:

1. 计算先验概率及条件概率
2. 对于给定实例,计算后验概率
3. 确定实例的类别

# R语言实现朴素贝叶斯
library(e1071)

nb_model <- naiveBayes(x_train, y_train)
predictions <- predict(nb_model, x_test)

决策树

决策树是一种基本的分类与回归方法。决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程;在回归问题中,表示将输入空间划分为单元,并在每个单元上确定输出值的过程。

决策树学习的三个步骤是:特征选择、决策树的生成和决策树的修剪。

特征选择的常用准则有:

1. 信息增益
2. 信息增益比
3. 基尼指数

ID3算法使用信息增益选择特征,C4.5算法使用信息增益比选择特征,CART算法使用基尼指数选择特征。

决策树生成算法的基本思路是:

1. 对数据集选择一个最优特征
2. 按该特征的不同取值将数据集分割成子集
3. 对子集重复步骤1、2,直到满足停止条件

为了防止过拟合,通常需要对生成的决策树进行剪枝。剪枝的基本策略是:从已生成的树上剪掉一些子树或叶节点,并将其根节点或父节点作为新的叶节点,使决策树变小。

# R语言实现决策树
library(rpart)

dt_model <- rpart(formula, data = train_data, method = "class")
predictions <- predict(dt_model, test_data, type = "class")

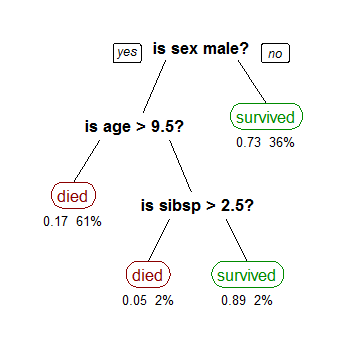
逻辑斯蒂回归与最大熵模型

逻辑斯蒂回归是一种常用的分类方法,可以看作是感知机的推广。逻辑斯蒂回归模型是:

P(Y=1|x) = 1 / (1 + exp(-(w·x + b)))

逻辑斯蒂回归的参数估计通常采用极大似然估计法。

最大熵模型是统计学习的重要方法,其核心思想是:在所有可能的概率模型中,熵最大的模型是最好的模型。最大熵模型的学习可以形式化为约束最优化问题,通常采用改进的迭代尺度法(IIS)或拟牛顿法求解。

# R语言实现逻辑斯蒂回归
glm_model <- glm(formula, data = train_data, family = binomial())
predictions <- predict(glm_model, newdata = test_data, type = "response")

支持向量机

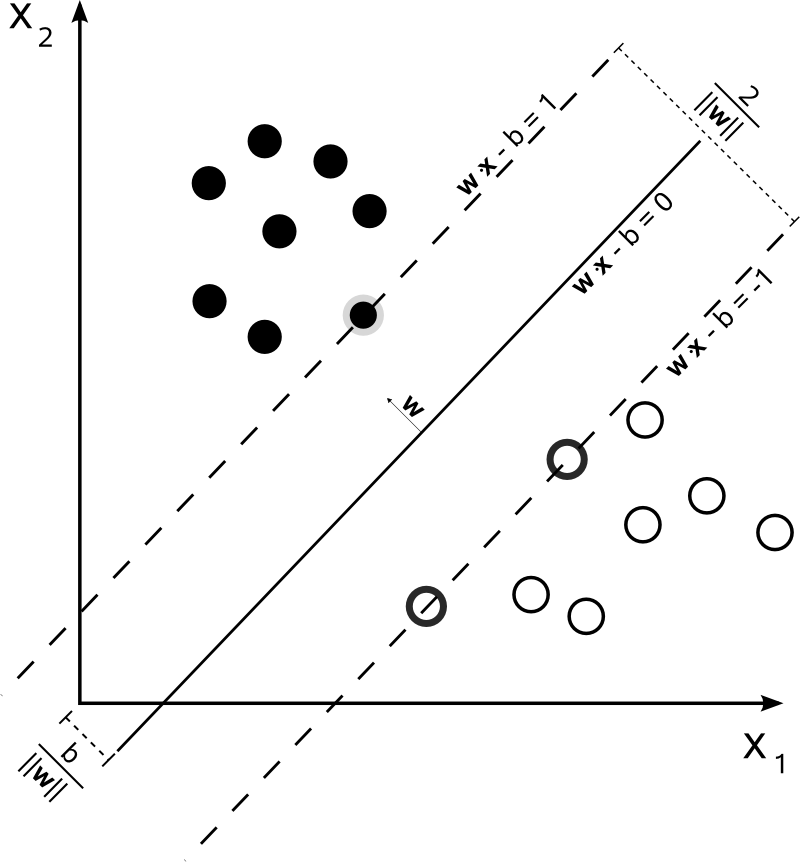
支持向量机(SVM)是一种二类分类模型,其基本模型是定义在特征空间上的间隔最大的线性分类器。SVM的学习策略是间隔最大化,可形式化为一个求解凸二次规划的问题。

SVM的基本思想是:求解能够正确划分训练数据集并且几何间隔最大的分离超平面。SVM的优势在于:

1. 有严格的数学理论支持
2. 能够处理高维数据
3. 解是稀疏的
4. 能有效避免过拟合

当训练数据线性不可分时,可以使用核技巧将原特征空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。常用的核函数包括:

1. 线性核
2. 多项式核
3. 高斯核(RBF核)
4. sigmoid核

# R语言实现SVM
library(e1071)

svm_model <- svm(formula, data = train_data, kernel = "radial")
predictions <- predict(svm_model, newdata = test_data)

集成学习

集成学习通过构建并结合多个学习器来完成学习任务,有效地提高了学习系统的泛化能力。常见的集成学习方法包括Bagging、Boosting和Random Forest等。

Bagging的基本思想是从原始数据集中有放回地随机抽取多个训练集,分别在各个训练集上训练出基学习器,再将这些基学习器进行结合。Random Forest是Bagging的一个变体,它在决策树的训练过程中引入了随机属性选择。

Boosting的思想是将弱学习器提升为强学习器。其代表算法AdaBoost的基本流程是:

1. 初始化训练数据的权值分布
2. 训练弱学习器
3. 计算弱学习器的错误率,更新数据权值分布
4. 将弱学习器线性组合

# R语言实现Random Forest
library(randomForest)

rf_model <- randomForest(formula, data = train_data)
predictions <- predict(rf_model, newdata = test_data)

总结

本文详细介绍了《统计学习方法》一书中的核心算法,包括感知机、k近邻、朴素贝叶斯、决策树、逻辑斯蒂回归、支持向量机等,并给出了相应的R语言实现。这些算法构成了机器学习的基础,对于理解更复杂的算法和模型至关重要。

在实际应用中,需要根据具体问题选择合适的算法。同时,数据预处理、特征工程、模型评估和调优等步骤也是机器学习过程中不可或缺的环节。希望本文能够帮助读者更好地理解统计学习方法,并在实践中灵活运用。