hurst

Hurst指数评估和R/S分析

hurst是一个用于分析__随机游走__和评估__Hurst指数(H)__的小型Python模块。

H = 0.5 — 布朗运动，
0.5 < H < 1.0 — 持续性行为，
0 < H < 0.5 — 反持续性行为。

安装

使用以下命令安装hurst模块
pip install hurst
或者
pip install -e git+https://github.com/Mottl/hurst#egg=hurst

使用方法

import numpy as np
import matplotlib.pyplot as plt
from hurst import compute_Hc, random_walk

# 使用random_walk()函数或手动生成随机游走序列：
# series = random_walk(99999, cumprod=True)
np.random.seed(42)
random_changes = 1. + np.random.randn(99999) / 1000.
series = np.cumprod(random_changes)  # 从随机变化创建随机游走

# 评估Hurst方程
H, c, data = compute_Hc(series, kind='price', simplified=True)

# 绘图
f, ax = plt.subplots()
ax.plot(data[0], c*data[0]**H, color="deepskyblue")
ax.scatter(data[0], data[1], color="purple")
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel('时间间隔')
ax.set_ylabel('R/S比率')
ax.grid(True)
plt.show()

print("H={:.4f}, c={:.4f}".format(H,c))

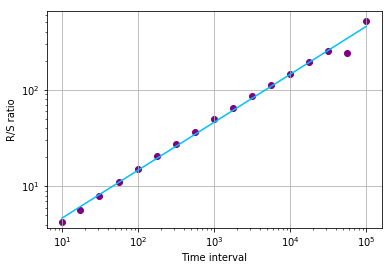
H=0.4964, c=1.4877

序列类型

compute_Hc函数的kind参数可以具有以下值：
'change'：序列仅为随机值（如np.random.randn(...)）
'random_walk'：序列为变化的累积和（如np.cumsum(np.random.randn(...))）
'price'：序列为变化的累积乘积（如np.cumprod(1+epsilon*np.random.randn(...))

布朗运动、持续性和反持续性随机游走

您可以使用random_walk()函数生成随机游走，如下所示：

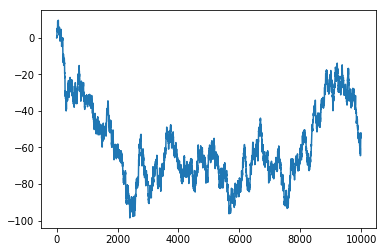
布朗运动

brownian = random_walk(99999, proba=0.5)

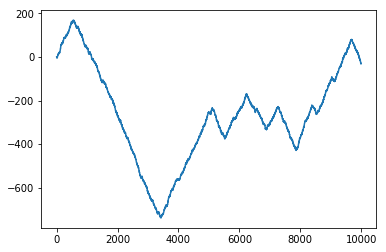
持续性

persistent = random_walk(99999, proba=0.7)

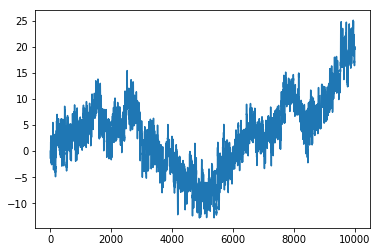
反持续性

antipersistent = random_walk(99999, proba=0.3)