GPU 难题

作者：Sasha Rush - srush_nlp

GPU 架构对机器学习至关重要，而且似乎每天都变得更加重要。然而，你可以成为机器学习专家而不需要接触 GPU 代码。通过抽象层面来获得直觉是很困难的。

这个笔记本试图以一种完全交互的方式教授初学者 GPU 编程。它不是提供概念性的文字说明，而是直接让你编写和构建 GPU 内核。这些练习使用 NUMBA，它可以将 Python 代码直接映射到 CUDA 内核。它看起来像 Python，但基本上与编写底层 CUDA 代码相同。我认为你可以在几个小时内从基础知识入手，理解当今 99% 深度学习背后的实际算法。如果你想阅读手册，可以在这里找到：

NUMBA CUDA 指南

我建议在 Colab 中完成这些练习，因为它很容易上手。请确保创建自己的副本，在设置中开启 GPU 模式（运行时 / 更改运行时类型，然后将硬件加速器设置为GPU），然后开始编码。

（如果你喜欢这种类型的难题，也可以看看我的 Tensor 难题，适用于 PyTorch。）

详细指南

!pip install -qqq git+https://github.com/danoneata/chalk@srush-patch-1
!wget -q https://github.com/srush/GPU-Puzzles/raw/main/robot.png https://github.com/srush/GPU-Puzzles/raw/main/lib.py

import numba
import numpy as np
import warnings
from lib import CudaProblem, Coord

warnings.filterwarnings(
    action="ignore", category=numba.NumbaPerformanceWarning, module="numba"
)

难题 1：映射

实现一个"内核"（GPU 函数），将向量 a 的每个位置加 10，并将结果存储在向量 out 中。每个位置使用 1 个线程。

警告这段代码看起来像 Python，但实际上是 CUDA！你不能使用标准的 Python 工具，如列表推导式，也不能获取 Numpy 属性，如形状或大小（如果你需要大小，它会作为参数给出）。这些难题只需要进行简单的操作，基本上是 +、*、简单的数组索引、for 循环和 if 语句。你可以使用局部变量。如果你遇到错误，可能是因为你做了一些复杂的操作 :)。

提示：把函数 call 看作是为每个线程运行一次。唯一的区别是每次 cuda.threadIdx.x 都会改变。

def map_spec(a):
    return a + 10


def map_test(cuda):
    def call(out, a) -> None:
        local_i = cuda.threadIdx.x
        # 在此填写代码（大约 1 行）

    return call


SIZE = 4
out = np.zeros((SIZE,))
a = np.arange(SIZE)
problem = CudaProblem(
    "Map", map_test, [a], out, threadsperblock=Coord(SIZE, 1), spec=map_spec
)
problem.show()

# 映射
 
   每线程最高分数：
   |  全局读取 | 全局写入 |  共享读取 | 共享写入 |
   |         0 |       0 |         0 |       0 |

svg

problem.check()

测试失败。
你的结果：[0. 0. 0. 0.]
预期结果：[10 11 12 13]

难题 2 - 压缩

实现一个内核，将 a 和 b 的每个位置相加，并将结果存储在 out 中。每个位置使用 1 个线程。

def zip_spec(a, b):
    return a + b


def zip_test(cuda):
    def call(out, a, b) -> None:
        local_i = cuda.threadIdx.x
        # 在此填写代码（大约 1 行）

    return call


SIZE = 4
out = np.zeros((SIZE,))
a = np.arange(SIZE)
b = np.arange(SIZE)
problem = CudaProblem(
    "Zip", zip_test, [a, b], out, threadsperblock=Coord(SIZE, 1), spec=zip_spec
)
problem.show()

# 压缩
 
   每线程最高分数：
   |  全局读取 | 全局写入 |  共享读取 | 共享写入 |
   |         0 |       0 |         0 |       0 |

svg

problem.check()

测试失败。
你的结果：[0. 0. 0. 0.]
预期结果：[0 2 4 6]

难题 3 - 保护

实现一个内核，将 a 的每个位置加 10，并将结果存储在 out 中。线程数量多于位置数量。

def map_guard_test(cuda):
    def call(out, a, size) -> None:
        local_i = cuda.threadIdx.x
        # 在此填写代码（大约 2 行）

    return call


SIZE = 4
out = np.zeros((SIZE,))
a = np.arange(SIZE)
problem = CudaProblem(
    "Guard",
    map_guard_test,
    [a],
    out,
    [SIZE],
    threadsperblock=Coord(8, 1),
    spec=map_spec,
)
problem.show()

# 保护
 
   每线程最高分数：
   |  全局读取 | 全局写入 |  共享读取 | 共享写入 |
   |         0 |       0 |         0 |       0 |

svg

problem.check()

测试失败。
你的结果：[0. 0. 0. 0.]
预期结果：[10 11 12 13]

难题 4 - 2D 映射

实现一个内核，将 a 的每个位置加 10，并将结果存储在 out 中。输入 a 是二维的且为正方形。线程数量多于位置数量。

def map_2D_test(cuda):
    def call(out, a, size) -> None:
        local_i = cuda.threadIdx.x
        local_j = cuda.threadIdx.y
        # 在此填写代码（大约 2 行）

    return call


SIZE = 2
out = np.zeros((SIZE, SIZE))
a = np.arange(SIZE * SIZE).reshape((SIZE, SIZE))
problem = CudaProblem(
    "Map 2D", map_2D_test, [a], out, [SIZE], threadsperblock=Coord(3, 3), spec=map_spec
)
problem.show()

# 2D 映射
 
   每线程最高分数：
   |  全局读取 | 全局写入 |  共享读取 | 共享写入 |
   |         0 |       0 |         0 |       0 |

svg

problem.check()

测试失败。
你的结果：[[0. 0.]
 [0. 0.]]
预期结果：[[10 11]
 [12 13]]

难题 5 - 广播

实现一个内核，将 a 和 b 相加，并将结果存储在 out 中。输入 a 和 b 是向量。线程数量多于位置数量。

def broadcast_test(cuda):
    def call(out, a, b, size) -> None:
        local_i = cuda.threadIdx.x
        local_j = cuda.threadIdx.y
        # 在此填写代码（大约 2 行）

    return call


SIZE = 2
out = np.zeros((SIZE, SIZE))
a = np.arange(SIZE).reshape(SIZE, 1)
b = np.arange(SIZE).reshape(1, SIZE)
problem = CudaProblem(
    "Broadcast",
    broadcast_test,
    [a, b],
    out,
    [SIZE],
    threadsperblock=Coord(3, 3),
    spec=zip_spec,
)
problem.show()

广播

分数(每线程最大值): | 全局读取 | 全局写入 | 共享读取 | 共享写入 | | 0 | 0 | 0 | 0 |

svg

problem.check()

测试失败。你的结果: [[0. 0.] [0. 0.]] 规范结果: [[0 1] [1 2]]

谜题 6 - 块

实现一个内核,将 a 的每个位置加 10 并存储在 out 中。每个块的线程数少于 a 的大小。

提示: 一个块是一组线程。每个块的线程数是有限的,但我们可以有很多不同的块。变量 cuda.blockIdx 告诉我们当前在哪个块中。

def map_block_test(cuda):
    def call(out, a, size) -> None:
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        # 在此填写代码(大约2行)

    return call


SIZE = 9
out = np.zeros((SIZE,))
a = np.arange(SIZE)
problem = CudaProblem(
    "Blocks",
    map_block_test,
    [a],
    out,
    [SIZE],
    threadsperblock=Coord(4, 1),
    blockspergrid=Coord(3, 1),
    spec=map_spec,
)
problem.show()

块

分数(每线程最大值): | 全局读取 | 全局写入 | 共享读取 | 共享写入 | | 0 | 0 | 0 | 0 |

svg

problem.check()

测试失败。你的结果: [0. 0. 0. 0. 0. 0. 0. 0. 0.] 规范结果: [10 11 12 13 14 15 16 17 18]

谜题 7 - 2D块

在2D中实现相同的内核。在两个方向上,每个块的线程数都少于 a 的大小。

def map_block2D_test(cuda):
    def call(out, a, size) -> None:
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        # 在此填写代码(大约4行)

    return call


SIZE = 5
out = np.zeros((SIZE, SIZE))
a = np.ones((SIZE, SIZE))

problem = CudaProblem(
    "Blocks 2D",
    map_block2D_test,
    [a],
    out,
    [SIZE],
    threadsperblock=Coord(3, 3),
    blockspergrid=Coord(2, 2),
    spec=map_spec,
)
problem.show()

2D块

分数(每线程最大值): | 全局读取 | 全局写入 | 共享读取 | 共享写入 | | 0 | 0 | 0 | 0 |

svg

problem.check()

测试失败。你的结果: [[0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.]] 规范结果: [[11. 11. 11. 11. 11.] [11. 11. 11. 11. 11.] [11. 11. 11. 11. 11.] [11. 11. 11. 11. 11.] [11. 11. 11. 11. 11.]]

谜题 8 - 共享

实现一个内核,将 a 的每个位置加 10 并存储在 out 中。每个块的线程数少于 a 的大小。

警告: 每个块只能有固定数量的共享内存,该块中的线程可以读写。这需要是一个字面的 Python 常量,而不是变量。写入共享内存后,你需要调用 cuda.syncthreads 以确保线程不会交叉。

(这个例子实际上并不需要共享内存或 syncthreads,但它是一个演示。)

TPB = 4
def shared_test(cuda):
    def call(out, a, size) -> None:
        shared = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x

        if i < size:
            shared[local_i] = a[i]
            cuda.syncthreads()

        # 在此填写代码(大约2行)

    return call


SIZE = 8
out = np.zeros(SIZE)
a = np.ones(SIZE)
problem = CudaProblem(
    "Shared",
    shared_test,
    [a],
    out,
    [SIZE],
    threadsperblock=Coord(TPB, 1),
    blockspergrid=Coord(2, 1),
    spec=map_spec,
)
problem.show()

共享

分数(每线程最大值): | 全局读取 | 全局写入 | 共享读取 | 共享写入 | | 1 | 0 | 0 | 1 |

svg

problem.check()

测试失败。你的结果: [0. 0. 0. 0. 0. 0. 0. 0.] 规范结果: [11. 11. 11. 11. 11. 11. 11. 11.]

谜题 9 - 池化

实现一个内核,将 a 的最后3个位置相加并存储在 out 中。每个位置有1个线程。每个线程只需要1次全局读取和1次全局写入。

提示: 记得要小心同步。

def pool_spec(a):
    out = np.zeros(*a.shape)
    for i in range(a.shape[0]):
        out[i] = a[max(i - 2, 0) : i + 1].sum()
    return out


TPB = 8
def pool_test(cuda):
    def call(out, a, size) -> None:
        shared = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        # 在此填写代码(大约8行)

    return call


SIZE = 8
out = np.zeros(SIZE)
a = np.arange(SIZE)
problem = CudaProblem(
    "Pooling",
    pool_test,
    [a],
    out,
    [SIZE],
    threadsperblock=Coord(TPB, 1),
    blockspergrid=Coord(1, 1),
    spec=pool_spec,
)
problem.show()

池化

分数(每线程最大值): | 全局读取 | 全局写入 | 共享读取 | 共享写入 | | 0 | 0 | 0 | 0 |

svg

problem.check()

测试失败。你的结果: [0. 0. 0. 0. 0. 0. 0. 0.] 规范结果: [ 0. 1. 3. 6. 9. 12. 15. 18.]

谜题 10 - 点积

实现一个内核,计算 a 和 b 的点积并将结果存储在 out 中。每个位置有1个线程。每个线程只需要2次全局读取和1次全局写入。

注意: 对于这个问题,你不需要担心共享读取的次数。我们稍后会处理这个挑战。

def dot_spec(a, b):
    return a @ b

TPB = 8
def dot_test(cuda):
    def call(out, a, b, size) -> None:
        shared = cuda.shared.array(TPB, numba.float32)

        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        # 在此填写代码(大约9行)
    return call
SIZE = 8
out = np.zeros(1)
a = np.arange(SIZE)
b = np.arange(SIZE)
problem = CudaProblem(
    "点积",
    dot_test,
    [a, b],
    out,
    [SIZE],
    threadsperblock=Coord(SIZE, 1),
    blockspergrid=Coord(1, 1),
    spec=dot_spec,
)
problem.show()

# 点积
 
   每线程最高得分:
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果: [0.]
规范结果: 140

题目11 - 一维卷积

实现一个计算 a 和 b 之间一维卷积并存储在 out 中的内核。你需要处理一般情况。每个线程只需要2次全局读取和1次全局写入。

def conv_spec(a, b):
    out = np.zeros(*a.shape)
    len = b.shape[0]
    for i in range(a.shape[0]):
        out[i] = sum([a[i + j] * b[j] for j in range(len) if i + j < a.shape[0]])
    return out


MAX_CONV = 4
TPB = 8
TPB_MAX_CONV = TPB + MAX_CONV
def conv_test(cuda):
    def call(out, a, b, a_size, b_size) -> None:
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x

        # 在此填写代码 (大约17行)

    return call


# 测试1

SIZE = 6
CONV = 3
out = np.zeros(SIZE)
a = np.arange(SIZE)
b = np.arange(CONV)
problem = CudaProblem(
    "一维卷积 (简单)",
    conv_test,
    [a, b],
    out,
    [SIZE, CONV],
    Coord(1, 1),
    Coord(TPB, 1),
    spec=conv_spec,
)
problem.show()

# 一维卷积 (简单)
 
   每线程最高得分:
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果: [0. 0. 0. 0. 0. 0.]
规范结果: [ 5.  8. 11. 14.  5.  0.]

测试2

out = np.zeros(15)
a = np.arange(15)
b = np.arange(4)
problem = CudaProblem(
    "一维卷积 (完整)",
    conv_test,
    [a, b],
    out,
    [15, 4],
    Coord(2, 1),
    Coord(TPB, 1),
    spec=conv_spec,
)
problem.show()

# 一维卷积 (完整)
 
   每线程最高得分:
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果: [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
规范结果: [14. 20. 26. 32. 38. 44. 50. 56. 62. 68. 74. 80. 41. 14.  0.]

题目12 - 前缀和

实现一个计算 a 的和并存储在 out 中的内核。如果 a 的大小大于块大小，则只存储每个块的和。

我们将使用共享内存中的并行前缀和算法来实现这一点。即算法的每一步应该将剩余数字的一半相加。请按照下图所示：

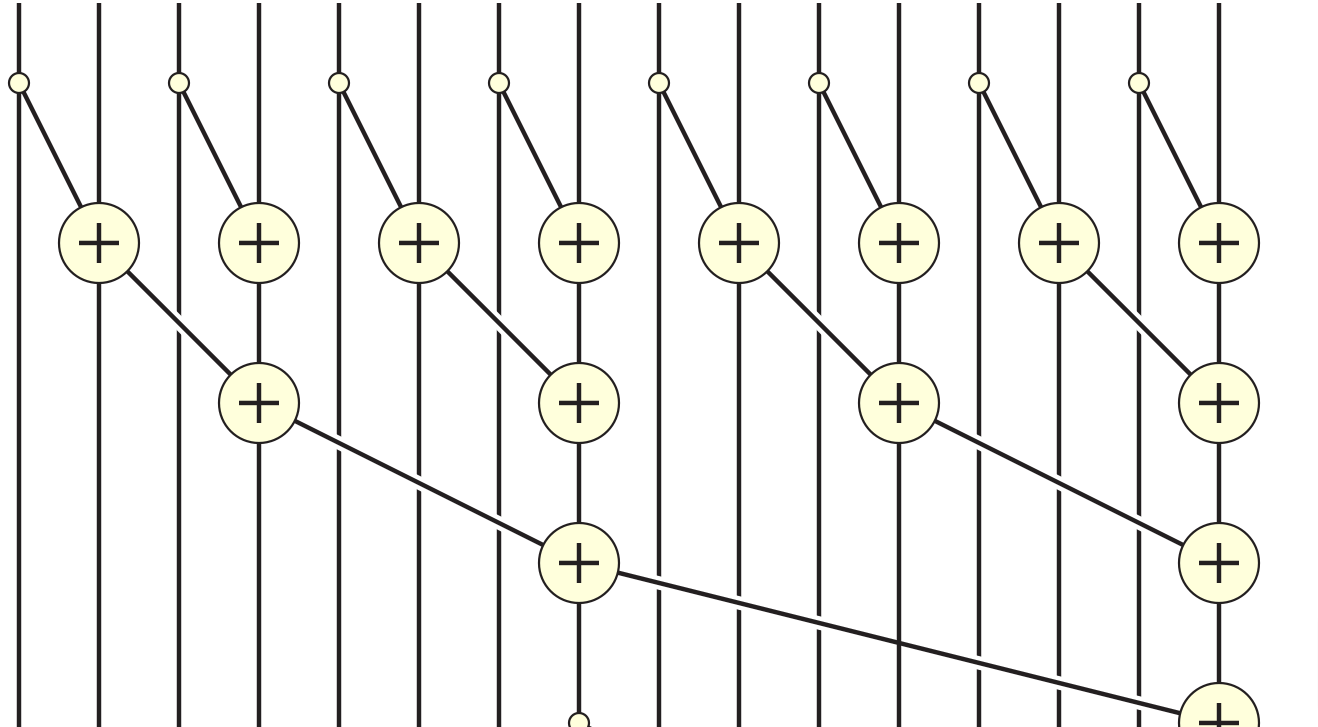
TPB = 8
def sum_spec(a):
    out = np.zeros((a.shape[0] + TPB - 1) // TPB)
    for j, i in enumerate(range(0, a.shape[-1], TPB)):
        out[j] = a[i : i + TPB].sum()
    return out


def sum_test(cuda):
    def call(out, a, size: int) -> None:
        cache = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        # 在此填写代码 (大约12行)

    return call


# 测试1

SIZE = 8
out = np.zeros(1)
inp = np.arange(SIZE)
problem = CudaProblem(
    "求和 (简单)",
    sum_test,
    [inp],
    out,
    [SIZE],
    Coord(1, 1),
    Coord(TPB, 1),
    spec=sum_spec,
)
problem.show()

# 求和 (简单)
 
   每线程最高得分:
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果: [0.]
规范结果: [28.]

测试2

SIZE = 15
out = np.zeros(2)
inp = np.arange(SIZE)
problem = CudaProblem(
    "求和 (完整)",
    sum_test,
    [inp],
    out,
    [SIZE],
    Coord(2, 1),
    Coord(TPB, 1),
    spec=sum_spec,
)
problem.show()

# 求和 (完整)
 
   每线程最高得分:
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果: [0. 0.]
规范结果: [28. 77.]

题目13 - 轴向求和

实现一个计算 a 的每列之和并存储在 out 中的内核。

TPB = 8
def sum_spec(a):
    out = np.zeros((a.shape[0], (a.shape[1] + TPB - 1) // TPB))
    for j, i in enumerate(range(0, a.shape[-1], TPB)):
        out[..., j] = a[..., i : i + TPB].sum(-1)
    return out


def axis_sum_test(cuda):
    def call(out, a, size: int) -> None:
        cache = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        batch = cuda.blockIdx.y
        # 在此填写代码 (大约12行)

    return call


BATCH = 4
SIZE = 6
out = np.zeros((BATCH, 1))
inp = np.arange(BATCH * SIZE).reshape((BATCH, SIZE))
problem = CudaProblem(
    "轴向求和",
    axis_sum_test,
    [inp],
    out,
    [SIZE],
    Coord(1, BATCH),
    Coord(TPB, 1),
    spec=sum_spec,
)
problem.show()

# 轴向求和
 
   每线程最高得分:
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果: [[0.]
 [0.]
 [0.]
 [0.]]
规范结果: [[ 15.]
 [ 51.]
 [ 87.]
 [123.]]

谜题14 - 矩阵相乘!

实现一个内核，将方阵 a 和 b 相乘，并将结果存储在 out 中。

提示：这里最高效的算法是在计算每个单独的行列点积之前，将一个块复制到共享内存中。如果矩阵适合共享内存，这很容易做到。先完成这种情况。然后更新你的代码以计算部分点积，并迭代地移动你复制到共享内存中的部分。你应该能够在6次全局读取中完成困难的情况。

def matmul_spec(a, b):
    return a @ b


TPB = 3
def mm_oneblock_test(cuda):
    def call(out, a, b, size: int) -> None:
        a_shared = cuda.shared.array((TPB, TPB), numba.float32)
        b_shared = cuda.shared.array((TPB, TPB), numba.float32)

        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        j = cuda.blockIdx.y * cuda.blockDim.y + cuda.threadIdx.y
        local_i = cuda.threadIdx.x
        local_j = cuda.threadIdx.y
        # 在此填写代码（大约14行）

    return call

# 测试1

SIZE = 2
out = np.zeros((SIZE, SIZE))
inp1 = np.arange(SIZE * SIZE).reshape((SIZE, SIZE))
inp2 = np.arange(SIZE * SIZE).reshape((SIZE, SIZE)).T

problem = CudaProblem(
    "矩阵乘法（简单）",
    mm_oneblock_test,
    [inp1, inp2],
    out,
    [SIZE],
    Coord(1, 1),
    Coord(TPB, TPB),
    spec=matmul_spec,
)
problem.show(sparse=True)

# 矩阵乘法（简单）
 
   得分（每线程最大）：
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果：[[0. 0.]
 [0. 0.]]
规范结果：[[ 1  3]
 [ 3 13]]

测试2

SIZE = 8
out = np.zeros((SIZE, SIZE))
inp1 = np.arange(SIZE * SIZE).reshape((SIZE, SIZE))
inp2 = np.arange(SIZE * SIZE).reshape((SIZE, SIZE)).T

problem = CudaProblem(
    "矩阵乘法（完整）",
    mm_oneblock_test,
    [inp1, inp2],
    out,
    [SIZE],
    Coord(3, 3),
    Coord(TPB, TPB),
    spec=matmul_spec,
)
problem.show(sparse=True)

# 矩阵乘法（完整）
 
   得分（每线程最大）：
   | 全局读取 | 全局写入 | 共享读取 | 共享写入 |
   |        0 |        0 |        0 |        0 |

svg

problem.check()

测试失败。
你的结果：[[0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]]
规范结果：[[  140   364   588   812  1036  1260  1484  1708]
 [  364  1100  1836  2572  3308  4044  4780  5516]
 [  588  1836  3084  4332  5580  6828  8076  9324]
 [  812  2572  4332  6092  7852  9612 11372 13132]
 [ 1036  3308  5580  7852 10124 12396 14668 16940]
 [ 1260  4044  6828  9612 12396 15180 17964 20748]
 [ 1484  4780  8076 11372 14668 17964 21260 24556]
 [ 1708  5516  9324 13132 16940 20748 24556 28364]]