深度解析TorchSDE: PyTorch中的可微分随机微分方程求解器

TorchSDE简介:随机微分方程的PyTorch实现

TorchSDE是由Google Research开发的一个开源Python库,旨在为随机微分方程(SDE)提供高效、可扩展的求解器。作为PyTorch的扩展,TorchSDE继承了PyTorch的易用性和灵活性,同时为处理复杂的随机动力系统提供了强大的工具。

TorchSDE的核心特性

1. GPU加速: TorchSDE充分利用GPU计算能力,大幅提升求解SDE的速度。

2. 高效反向传播: 库实现了高效的灵敏度分析,使得基于SDE的深度学习模型训练变得可行。

3. 多种求解方法: 提供多种数值方法来求解SDE,适应不同类型的问题。

4. 与PyTorch生态系统无缝集成: 作为PyTorch的扩展,可以轻松与其他PyTorch模块结合使用。

5. 丰富的示例和文档: 提供了详细的使用说明和多个实际应用示例。

深入理解随机微分方程

随机微分方程(SDE)是描述随机动力系统的重要数学工具。与常微分方程(ODE)不同,SDE引入了随机性,使其能够更好地模拟现实世界中的不确定性。

SDE的基本形式

一个典型的SDE可以表示为:

dX(t) = f(X(t), t)dt + g(X(t), t)dW(t)

其中:

• X(t)是随时间变化的状态变量
• f(X(t), t)是确定性项(漂移项)
• g(X(t), t)是随机项(扩散项)
• W(t)是维纳过程(布朗运动)

TorchSDE提供了一种直观的方式来定义和求解这类方程。

TorchSDE的安装与基本使用

安装

TorchSDE可以通过pip轻松安装:

pip install torchsde

要求Python版本≥3.8,PyTorch版本≥1.6.0。

基本使用示例

以下是一个简单的SDE定义和求解示例:

import torch
import torchsde

class SDE(torch.nn.Module):
    noise_type = 'general'
    sde_type = 'ito'

    def __init__(self):
        super().__init__()
        self.mu = torch.nn.Linear(3, 3)
        self.sigma = torch.nn.Linear(3, 3 * 2)

    def f(self, t, y):
        return self.mu(y)  # 漂移项

    def g(self, t, y):
        return self.sigma(y).view(32, 3, 2)  # 扩散项

sde = SDE()
y0 = torch.full((32, 3), 0.1)  # 初始状态
ts = torch.linspace(0, 1, 20)  # 时间点

# 求解SDE
ys = torchsde.sdeint(sde, y0, ts)

这个例子定义了一个简单的SDE模型,并使用torchsde.sdeint函数求解。

TorchSDE的高级应用

TorchSDE不仅限于简单的SDE求解,它还支持多种高级应用,特别是在深度学习和随机建模领域。

1. 潜在SDE (Latent SDE)

潜在SDE是一种将SDE与变分推断结合的方法,可以用于学习复杂时间序列数据的潜在表示。TorchSDE提供了实现潜在SDE的示例,展示了如何将SDE用作变分自编码器的先验和近似后验。

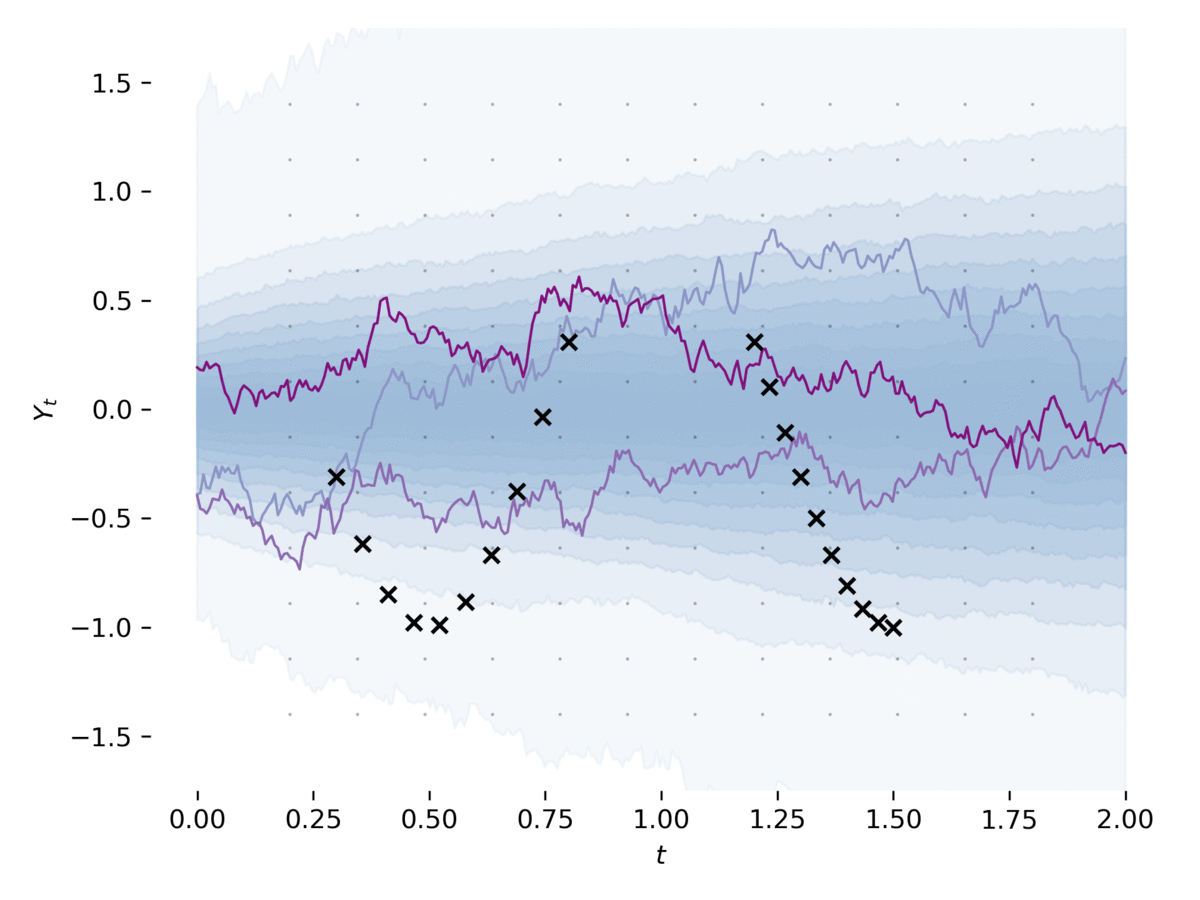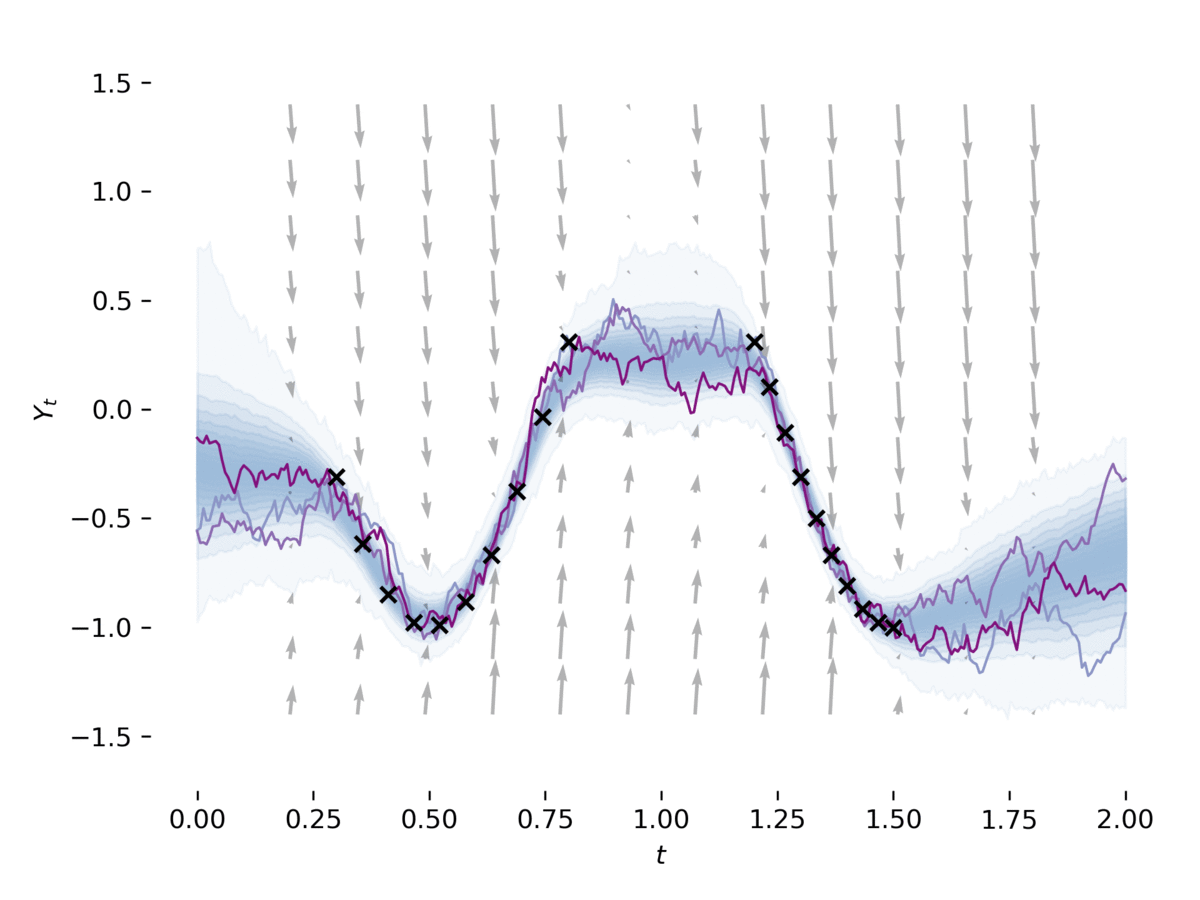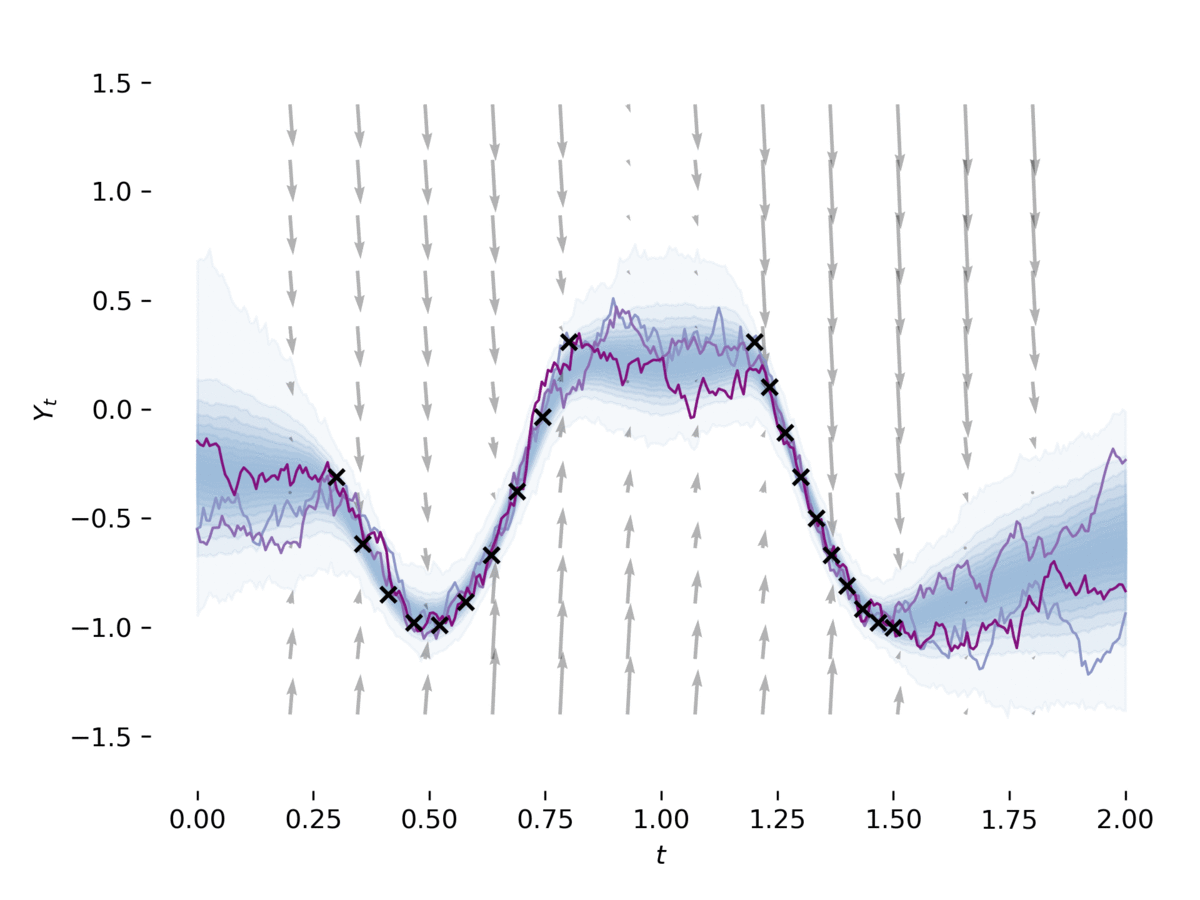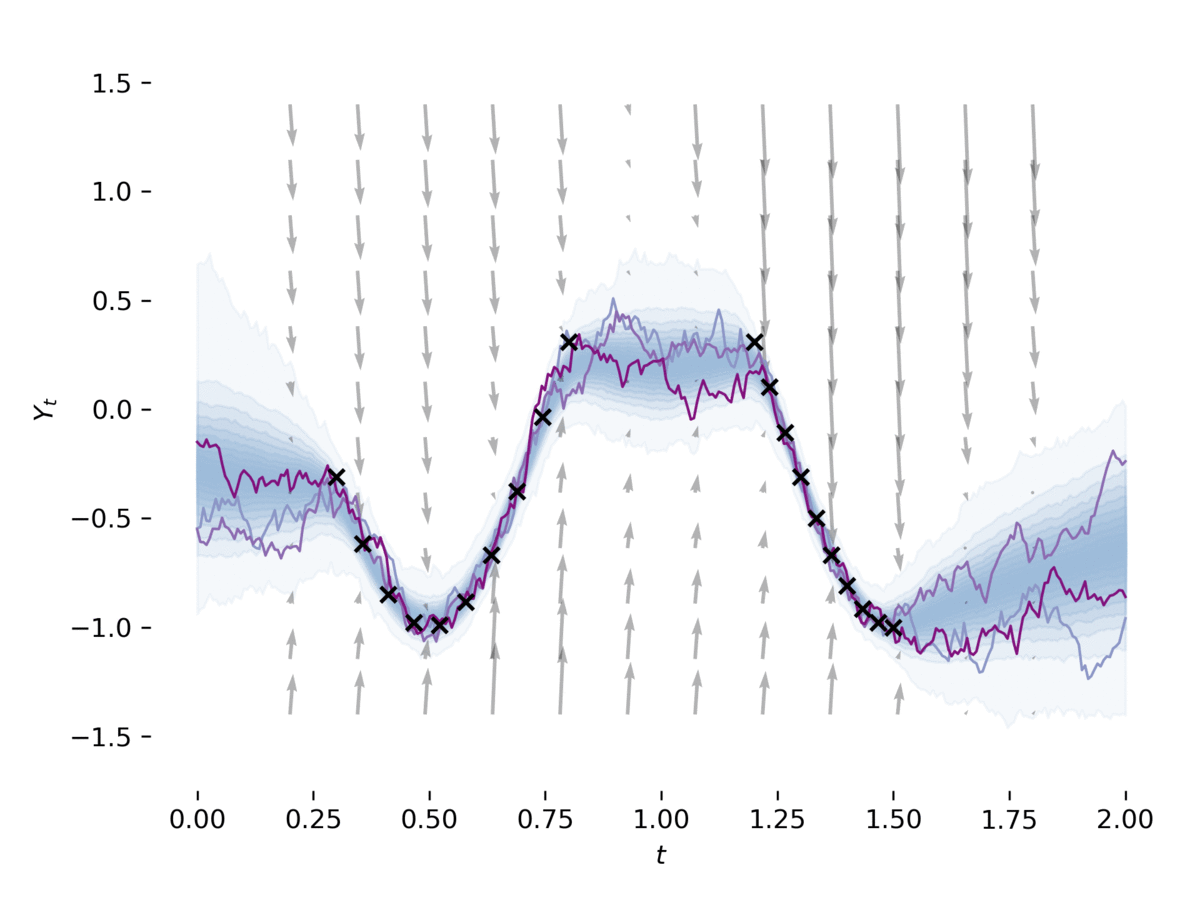
上图展示了使用潜在SDE学习的时间序列数据生成过程。

2. 神经SDE作为GAN

TorchSDE还支持将SDE用作生成对抗网络(GAN)的生成器。这种方法将连续时间随机过程与GAN框架结合,能够生成更加自然和连续的序列数据。

# SDE作为GAN生成器的简化示例
class SDEGenerator(torch.nn.Module):
    def __init__(self):
        super().__init__()
        # 定义SDE参数
    
def forward(self, t, y):
        # 实现SDE的漂移和扩散函数
        pass

# 使用神经CDE作为判别器
class NCDEDiscriminator(torch.nn.Module):
    def __init__(self):
        super().__init__()
        # 定义神经CDE参数
    
def forward(self, path):
        # 实现判别器逻辑
        pass

# 训练循环
generator = SDEGenerator()
discriminator = NCDEDiscriminator()
# ... GAN训练逻辑 ...

这种方法为生成连续时间序列数据提供了新的可能性。

TorchSDE在科学研究中的应用

TorchSDE不仅是一个技术工具,也是推动随机建模和深度学习研究前沿的重要基础。以下是几个TorchSDE在科研中的关键应用:

1. 金融建模: SDE在金融数学中扮演着核心角色,特别是在资产定价和风险管理方面。TorchSDE使得复杂金融模型的实现和校准变得更加高效。

2. 物理系统模拟: 许多物理系统本质上是随机的,如布朗运动、量子系统等。TorchSDE为这些系统提供了精确的数值模拟工具。

3. 生物系统建模: 在系统生物学中,SDE用于模拟基因调控网络和细胞信号通路。TorchSDE的高效计算能力使得大规模生物系统的模拟成为可能。

4. 气候模型: 气候系统的复杂性和不确定性使得SDE成为气候建模的有力工具。TorchSDE可以帮助研究人员更好地理解和预测气候变化。

5. 神经科学: 在神经科学中,SDE被用来模拟神经元活动和大脑网络动力学。TorchSDE为这一领域提供了灵活的建模框架。

TorchSDE的性能优化

TorchSDE不仅提供了功能强大的SDE求解器,还在性能方面做了大量优化,以满足大规模计算的需求。

GPU加速

TorchSDE充分利用了GPU的并行计算能力,大幅提升了SDE求解的速度。对于大规模的SDE系统或需要多次模拟的蒙特卡洛方法,GPU加速可以带来数量级的性能提升。

自动微分和反向传播

TorchSDE与PyTorch的自动微分系统深度集成,支持对SDE解的高效梯度计算。这使得基于SDE的深度学习模型能够高效训练,为随机控制和优化问题提供了强大工具。

内存优化

对于长时间序列或大规模系统,内存使用是一个关键问题。TorchSDE实现了多种内存优化技术,如检查点策略(checkpointing),使得即使在内存受限的情况下也能处理复杂的SDE问题。

TorchSDE的未来发展方向

作为一个活跃的开源项目,TorchSDE正在不断发展和改进。以下是一些潜在的未来发展方向:

1. 更多SDE类型支持: 扩展对更多类型SDE的支持,如跳跃扩散过程、分数SDE等。

2. 与其他深度学习架构的集成: 进一步探索SDE与其他深度学习架构(如transformer、图神经网络)的结合。

3. 分布式计算支持: 增加对大规模分布式计算的支持,以处理更大规模的SDE系统。

4. 领域特定优化: 针对特定应用领域(如金融、物理)提供优化的求解器和接口。

5. 可解释性工具: 开发工具来帮助理解和可视化SDE模型的行为和预测。

结语

TorchSDE为随机微分方程的数值求解和深度学习应用提供了一个强大而灵活的框架。它不仅是一个技术工具,更是推动随机建模和机器学习前沿研究的重要基础设施。随着深度学习和随机过程在各个领域的应用不断深入,TorchSDE将在科学计算、金融建模、物理模拟等多个方面发挥越来越重要的作用。

对于研究人员和工程师来说,掌握TorchSDE不仅能够提高处理随机动力系统的能力,还能为探索深度学习与随机过程结合的新前沿提供有力工具。随着项目的不断发展和社区的持续贡献,我们可以期待TorchSDE在未来带来更多exciting的可能性。