⚡️分阶段一致性模型⚡️
[论文] [项目主页 ✨] [🤗Hugging Face预训练模型] [演示] [Civitai]
作者:王富云1、黄照阳2、Alexander William Bergman3,6、沈大众4、 高鹏4、Michael Lingelbach3,6、孙可强1、边伟康1 宋广露5、刘宇4、李鸿升1、王晓刚1
1香港中文大学多媒体实验室 2Avolution AI 3Hedra 4上海人工智能实验室 5商汤科技 6斯坦福大学

@article{wang2024phased,
title={Phased Consistency Model},
author={Wang, Fu-Yun and Huang, Zhaoyang and Bergman, Alexander William and Shen, Dazhong and Gao, Peng and Lingelbach, Michael and Sun, Keqiang and Bian, Weikang and Song, Guanglu and Liu, Yu and others},
journal={arXiv preprint arXiv:2405.18407},
year={2024}
}
新闻
-
- 我们在CIFAR上的4步模型(无条件)达到了
FID 2.03。 - 我们在CIFAR上的8步模型(无条件)达到了
FID 1.94,Inception Score为10.05。 - 我们在ImageNet64上的4步模型(条件)达到了
FID 3.0,仅使用官方CM(4步使用LIPIPS损失:FID 4.3)的0.1%训练预算。
- 我们在CIFAR上的4步模型(无条件)达到了
- [2024.07.27]: 发布了使用Stable Diffusion XL的PCM-LoRA训练脚本。
- [2024.06.19]: 发布了使用Stable Diffusion 3的PCM-LoRA训练脚本。参见text_to_image_sd3。发布了Stable Diffusion 3的PCM-LORA权重。参见PCM_Weights。
| PCM-SD3-2步-确定性 | PCM-SD3-4步-确定性 | PCM-SD3-随机性(可视为更清晰的LCM) |
|---|---|---|
 |  |  |
- [2024.06.04]: Hugging Face演示已可使用。感谢@radames的贡献!
- [2024.06.01]: 在huggingface上发布了Stable Diffusion v1.5和Stable Diffusion XL的PCM-LoRA权重。
- [2024.06.01]: 发布了使用Stable Diffusion v1.5的PCM-LoRA训练脚本。参见tran_pcm_lora_sd15.sh。
我们使用8张A800显卡训练权重。但我初步实验结果表明,仅使用一张GPU也能取得不错的效果。
儿童节快乐!永远不会太老而无法庆祝童年的欢乐!
| HyperSD的单步生成对比 | PCM的单步生成对比 |
|---|---|
 |  |
| hypersd | 我们的方法 |
我们的模型在生成多样性方面明显优于同期工作HyperSD。
简介
分阶段一致性模型(PCM)可能是目前大型扩散模型中最强大的采样加速策略之一,用于快速文本条件图像生成。
一致性模型(CM),由杨松等人提出,是一种有前景的新型生成模型家族,可以在无条件和类别条件设置下用很少的步骤(通常是2步)生成高保真图像。之前的工作,潜在一致性模型(LCM),试图复制一致性模型在文本条件生成方面的能力,但通常无法达到令人满意的结果,特别是在低步骤范围(1~4步)。相反,我们认为PCM是原始一致性模型在高分辨率、文本条件图像生成方面更成功的扩展,更好地复制了原始一致性模型在更高级生成设置中的能力。
总的来说,我们发现(L)CM主要存在三个局限性:
- LCM在选择CFG方面缺乏灵活性,对负面提示不敏感。
- LCM无法在不同推理步骤下产生一致的结果。当步骤太多时(随机采样误差)或太少时(能力不足),其结果会变得模糊。
- LCM在低步骤范围内产生糟糕且模糊的结果。
这些局限性可以从下图中明显看出。
我们为高分辨率文本条件图像生成推广了一致性模型的设计空间,分析并解决了之前LCM工作中的局限性。

PF-ODE
从连续时间的角度来看,扩散模型实际上定义了一个前向条件概率路径,中间分布 $\mathbb P_{t}(\mathbf x | \mathbf x_0)$ 在 $\mathbf x_0$ 条件下的一般表示为 $\alpha_t \mathbf x_0 + \sigma_t \boldsymbol \epsilon \sim \mathcal N(\alpha_t\mathbf x_0, \sigma_{t}^2\mathbf I)$,这等同于随机微分方程 $\mathrm d\mathbf x_{t} = f_{t} \mathbf x_{t} \mathrm d t + g_{t} \mathrm d \boldsymbol w_{t}$,其中 $w_{t}$ 表示标准维纳过程。
对于前向 SDE,一个显著的特性是存在一个反向时间 ODE 轨迹,被 Song 等人称为 PF ODE,它不引入额外的随机性,仍然满足预定义的边缘分布,即:
$\mathrm d \mathbf x = (f_t - \frac{1}{2} g_{t}^2 \nabla_{\mathbf x} \log \mathbb P_{t}(\mathbf x)) \mathrm d t$,
其中 $\mathbb P_{t}(\mathbf x)= \mathbb E\left[\mathbb P_{t}(\mathbf x|\mathbf x_{0})| \mathbf x_{0}\right]$。扩散训练过程本质上使用深度神经网络 ($\boldsymbol s_{\theta}$) 训练一个得分估计器。
一般来说,反转 SDE 有无限多种可能的路径。然而,ODE 轨迹没有任何随机性,基本上更适合采样。在稳定扩散社区中应用的大多数调度器,包括 DDIM、DPM-solver、Euler 和 Heun 等,通常都基于更好地近似 ODE 轨迹的原则。大多数基于蒸馏的方法,包括 rectified-flow、guided distillation 等,也可以被视为用更大的步长更好地近似 ODE 轨迹(尽管大多数方法没有讨论相关部分)。
一致性模型旨在直接通过蒸馏或训练学习 ODE 轨迹的解点。
在 PCM 中,我们的工作重点是蒸馏,这通常更容易学习。对于训练,我们留待未来研究。
学习范式比较
一致性轨迹模型(CTM)指出,CM 在应用于多步采样以提高样本质量时存在随机性误差累积问题,并提出了一个更通用的框架,允许沿 ODE 轨迹的任意对移动。然而,它需要一个额外的目标时间步嵌入,这与传统扩散模型的设计空间不一致。此外,CTM 基本上更难训练。假设我们将 ODE 轨迹离散化为 N 个点,扩散模型和一致性模型的学习目标都是 $\mathcal O(N)$。然而,CTM 的学习目标数量是 $\mathcal O(N^2)$。我们提出的 PCM 也解决了随机性误差累积问题,但训练起来要容易得多。
我们方法的核心思想是将整个 ODE 轨迹分为多个子轨迹。 下图说明了扩散模型(DMs)、一致性模型(CMs)、一致性轨迹模型(CTMs)和我们提出的分阶段一致性模型(PCMs)之间的学习范式差异。
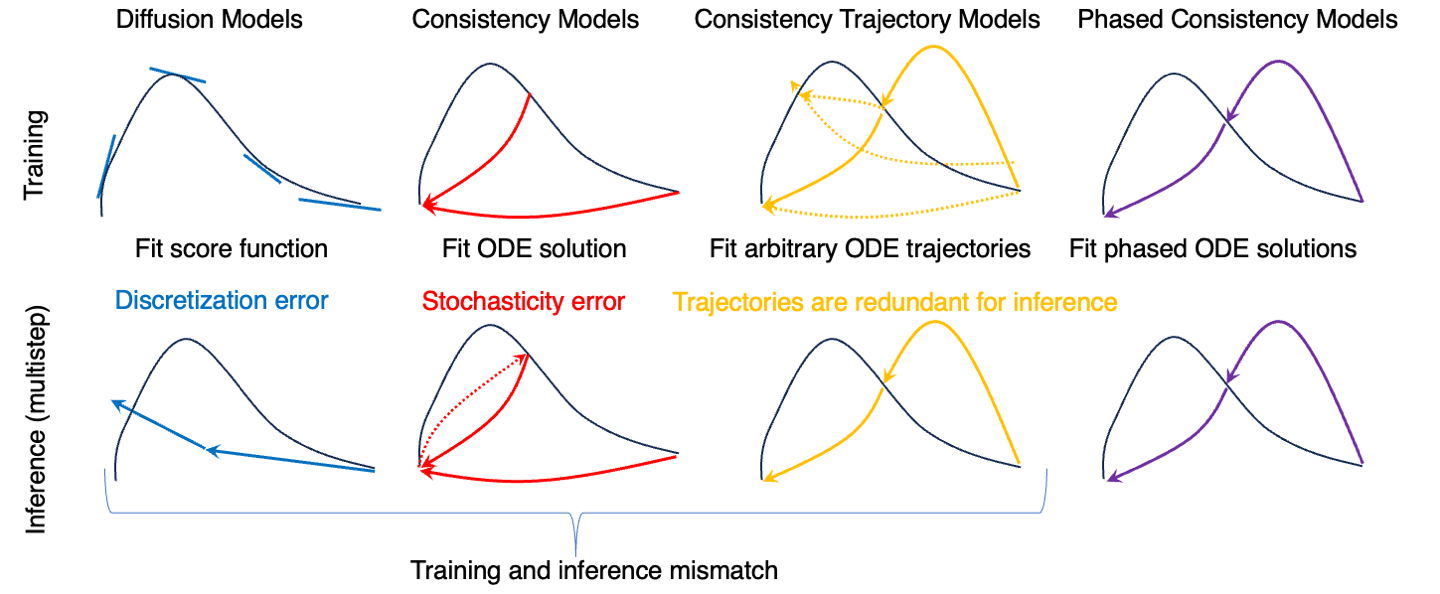
为了更好地比较,我们还实现了一个基线,我们称之为 simpleCTM。我们将 CTM 的高级思想从 k-diffusion 框架适配到具有稳定扩散的 DDPM 框架中,并比较其性能。在使用相同资源进行训练时,我们的方法取得了显著优越的性能。
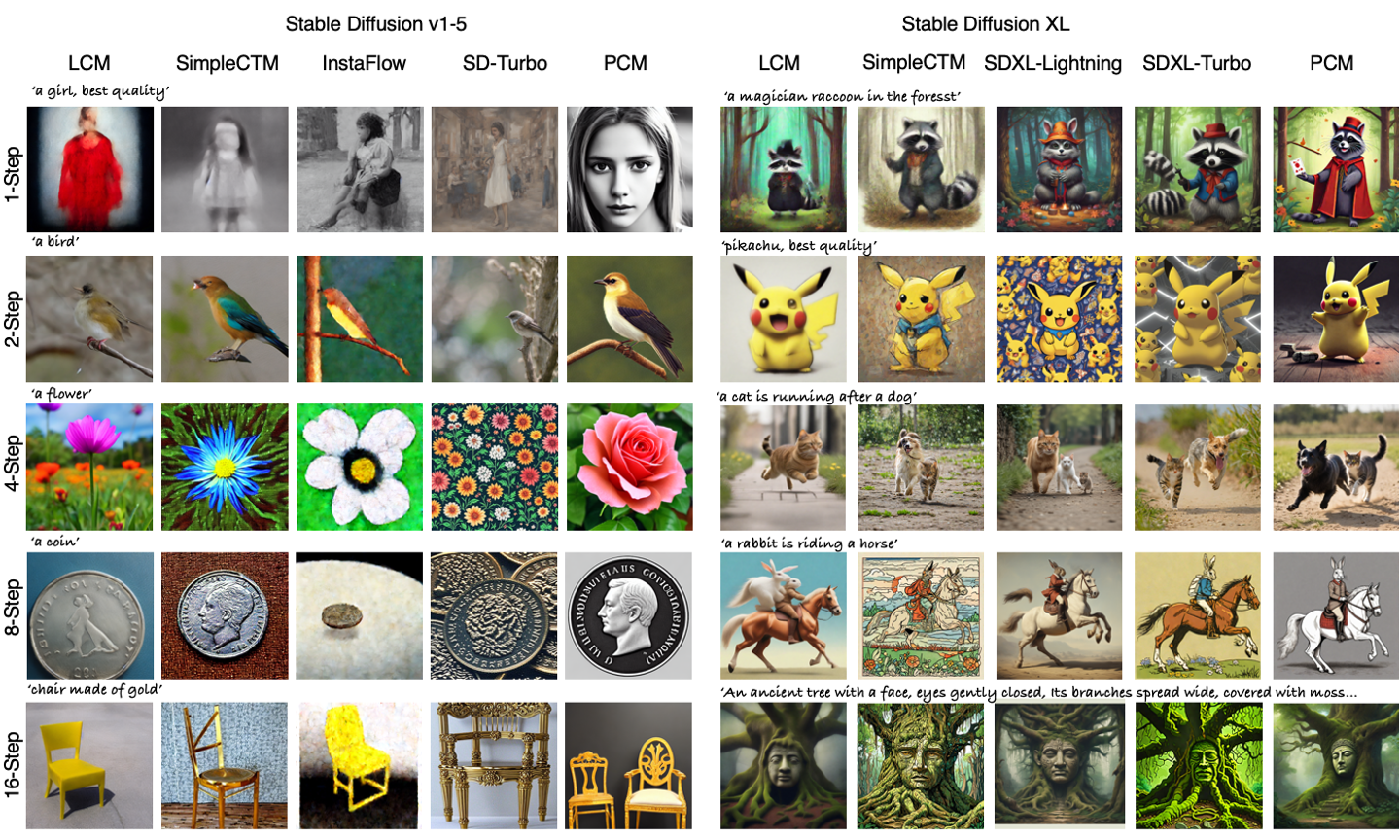
PCM 的样本
PCM 可以在 1、2、4、8、16 步内实现具有良好质量的文本条件图像合成。

对比
与当前可用的强大快速生成模型相比,PCM 实现了先进的生成结果,包括基于 GAN 的方法:SDXL-Turbo、SD-Turbo、SDXL-Lightning;基于 rectified-flow 的方法:InstaFlow;基于 CM 的方法:LCM、SimpleCTM。
联系与合作
如果您对代码有任何疑问,请随时与我联系!

 访问官网
访问官网 Github
Github Huggingface
Huggingface 论文
论文










