rliable

rliable 是一个开源 Python 库，用于对强化学习和机器学习基准进行可靠评估，即使只有少量运行结果。

要求	当前评估方法	我们的建议
总体性能的不确定性	点估计: <ul> <li> 忽视统计不确定性 </li> <li> 阻碍结果可重复性 </li></ul>	使用分层自助抽样置信区间 (CI) 的区间估计
跨任务和运行的性能变异性	任务平均分数表: <ul><li> 超过几个任务后难以理解 </li> <li> 经常省略标准差 </li> <li> 对多峰和重尾分布的描述不完整 </li> </ul>	分数分布 (性能曲线): <ul> <li> 显示跨任务所有运行的分数尾部分布 </li> <li> 允许定性比较 </li> <li> 易于读取任何分数百分位 </li> </ul>
总结基准性能的汇总指标	均值: <ul><li> 通常被异常任务的性能主导 </li></ul> 中位数: <ul> <li> 统计效率低（需要大量运行才能声称有改进） </li> <li> 整体性能指标不佳：近一半任务得分为 0 也不会改变 </li> </ul>	所有运行的四分位均值 (IQM): <ul> <li> 中间 50% 组合运行的性能 </li> <li> 对异常分数稳健，但统计效率高于中位数 </li> </ul> 为展示性能提升的其他方面，报告改进概率和最优性差距

rliable 提供以下支持：

分层自助抽样置信区间 (CI)
性能曲线（带绘图功能）
汇总指标
- 所有运行的四分位均值 (IQM)
- 最优性差距
- 改进概率

交互式 Colab

我们在 bit.ly/statistical_precipice_colab 提供了一个 Colab，展示了如何使用该库，并提供了在广泛使用的基准（包括 Atari 100k、ALE、DM Control 和 Procgen）上发布算法的示例。

Atari 100k、ALE、DM Control 和 Procgen 的单次运行数据

您可以通过此公共 GCP 存储桶访问单次运行的数据（您可能需要使用 Gmail 账户登录才能使用 Gcloud）：https://console.cloud.google.com/storage/browser/rl-benchmark-data。上述交互式 Colab 还允许您以编程方式访问数据。

论文

欲了解更多详情，请参阅随附的 NeurIPS 2021 论文（杰出论文奖）： Deep Reinforcement Learning at the Edge of the Statistical Precipice。

安装

要安装 rliable，请运行：

pip install -U rliable

要安装 rliable 的最新版本作为包，请运行：

pip install git+https://github.com/google-research/rliable

要导入 rliable，我们建议：

from rliable import library as rly
from rliable import metrics
from rliable import plot_utils

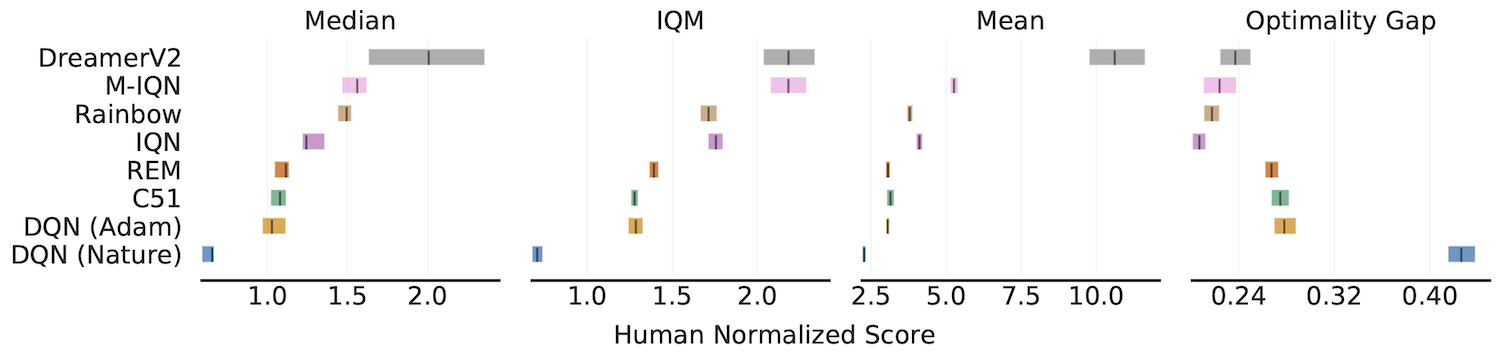
带有 95% 分层自助抽样置信区间的汇总指标

IQM、最优性差距、中位数、均值

algorithms = ['DQN (Nature)', 'DQN (Adam)', 'C51', 'REM', 'Rainbow',
              'IQN', 'M-IQN', 'DreamerV2']
# 加载 ALE 分数作为字典，将算法映射到其人类归一化
# 分数矩阵，每个矩阵的大小为 `(运行次数 x 游戏数)`。
atari_200m_normalized_score_dict = ...
aggregate_func = lambda x: np.array([
  metrics.aggregate_median(x),
  metrics.aggregate_iqm(x),
  metrics.aggregate_mean(x),
  metrics.aggregate_optimality_gap(x)])
aggregate_scores, aggregate_score_cis = rly.get_interval_estimates(
  atari_200m_normalized_score_dict, aggregate_func, reps=50000)
fig, axes = plot_utils.plot_interval_estimates(
  aggregate_scores, aggregate_score_cis,
  metric_names=['中位数', 'IQM', '均值', '最优性差距'],
  algorithms=algorithms, xlabel='人类归一化分数')

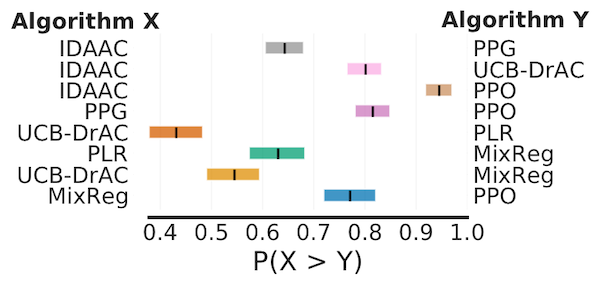
改进概率

# 将ProcGen分数加载为包含我们想要比较的算法对归一化分数矩阵对的字典
procgen_algorithm_pairs = {.. , 'x,y': (score_x, score_y), ..}
average_probabilities, average_prob_cis = rly.get_interval_estimates(
  procgen_algorithm_pairs, metrics.probability_of_improvement, reps=2000)
plot_utils.plot_probability_of_improvement(average_probabilities, average_prob_cis)

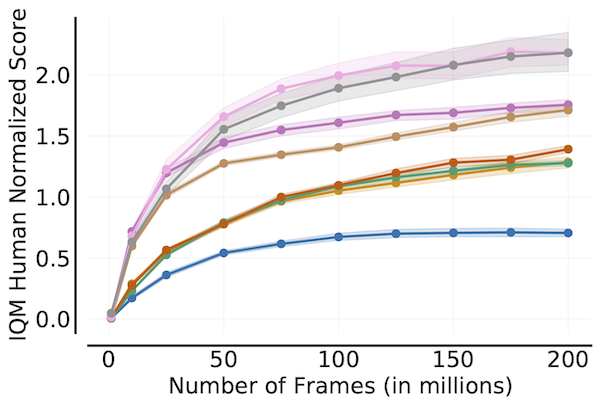
样本效率曲线

algorithms = ['DQN (Nature)', 'DQN (Adam)', 'C51', 'REM', 'Rainbow',
              'IQN', 'M-IQN', 'DreamerV2']
# 将ALE分数加载为字典，将算法映射到其在所有2亿帧中的人类归一化分数矩阵，
# 每个矩阵大小为`(运行次数 x 游戏数量 x 200)`，其中每百万帧记录一次分数。
ale_all_frames_scores_dict = ...
frames = np.array([1, 10, 25, 50, 75, 100, 125, 150, 175, 200]) - 1
ale_frames_scores_dict = {algorithm: score[:, :, frames] for algorithm, score
                          in ale_all_frames_scores_dict.items()}
iqm = lambda scores: np.array([metrics.aggregate_iqm(scores[..., frame])
                               for frame in range(scores.shape[-1])])
iqm_scores, iqm_cis = rly.get_interval_estimates(
  ale_frames_scores_dict, iqm, reps=50000)
plot_utils.plot_sample_efficiency_curve(
    frames+1, iqm_scores, iqm_cis, algorithms=algorithms,
    xlabel=r'帧数（百万）',
    ylabel='IQM人类归一化分数')

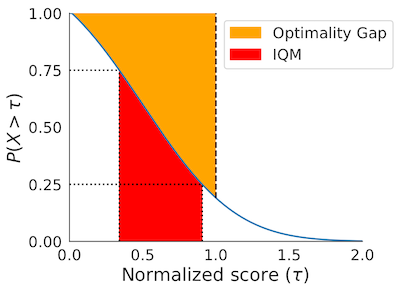
性能剖面

# 将ALE分数加载为字典，将算法映射到其人类归一化分数矩阵，
# 每个矩阵大小为`(运行次数 x 游戏数量)`。
atari_200m_normalized_score_dict = ...
# 人类归一化分数阈值
atari_200m_thresholds = np.linspace(0.0, 8.0, 81)
score_distributions, score_distributions_cis = rly.create_performance_profile(
    atari_200m_normalized_score_dict, atari_200m_thresholds)
# 绘制分数分布
fig, ax = plt.subplots(ncols=1, figsize=(7, 5))
plot_utils.plot_performance_profiles(
  score_distributions, atari_200m_thresholds,
  performance_profile_cis=score_distributions_cis,
  colors=dict(zip(algorithms, sns.color_palette('colorblind'))),
  xlabel=r'人类归一化分数 $(\tau)$',
  ax=ax)

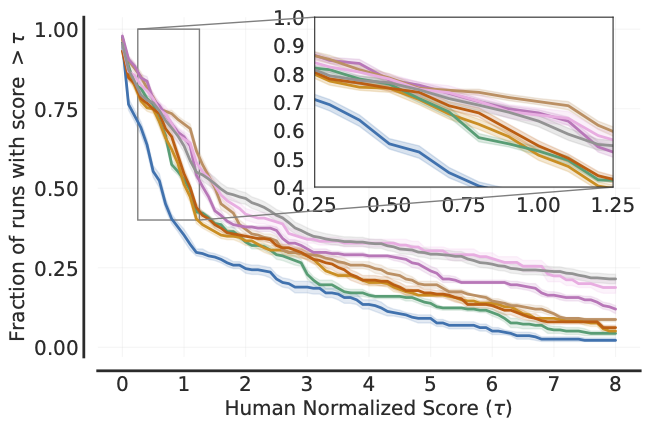
上述剖面也可以使用非线性缩放进行绘制，如下所示：

plot_utils.plot_performance_profiles(
  perf_prof_atari_200m, atari_200m_tau,
  performance_profile_cis=perf_prof_atari_200m_cis,
  use_non_linear_scaling=True,
  xticks = [0.0, 0.5, 1.0, 2.0, 4.0, 8.0]
  colors=dict(zip(algorithms, sns.color_palette('colorblind'))),
  xlabel=r'人类归一化分数 $(\tau)$',
  ax=ax)

依赖项

代码在Python>=3.7下测试，并使用以下包：

arch == 5.3.0
scipy >= 1.7.0
numpy >= 0.9.0
absl-py >= 1.16.4
seaborn >= 0.11.2

引用

如果您发现这个开源发布有用，请在您的论文中引用：

@article{agarwal2021deep,
  title={Deep Reinforcement Learning at the Edge of the Statistical Precipice},
  author={Agarwal, Rishabh and Schwarzer, Max and Castro, Pablo Samuel
          and Courville, Aaron and Bellemare, Marc G},
  journal={Advances in Neural Information Processing Systems},
  year={2021}
}

免责声明：这不是谷歌的官方产品。