MarkovJunior
MarkovJunior是一种概率性编程语言,程序是重写规则的组合,推理通过约束传播执行。MarkovJunior以数学家Andrey Andreyevich Markov命名,他定义并研究了现在被称为马尔可夫算法的内容。


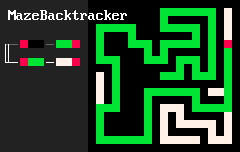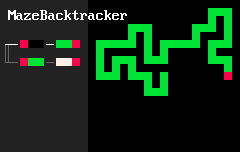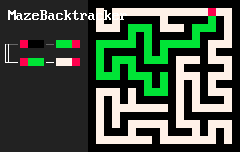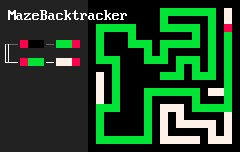
在基本形式中,一个MarkovJunior程序是一个有序的重写规则列表。例如,MazeBacktracker(左下动画)是一个包含2条重写规则的列表:
RBB=GGR或"用绿绿红替换红黑黑"。RGG=WWR或"用白白红替换红绿绿"。
在每个执行步骤中,MJ解释器都会找到列表中第一个在网格上有匹配的规则,找到该规则的所有匹配项并随机应用该规则。在迷宫回溯示例中,解释器首先应用一系列 RBB=GGR规则。但最终绿色自避免行走会陷入困境。此时第一个规则没有匹配,所以解释器应用第二个规则RGG=WWR直到行走摆脱困境。然后它可以再次应用第一个规则,依此类推。当没有任何规则有匹配时,解释器停止。

MarkovJunior中的概率推理允许对未来状态施加约束,并仅生成满足约束的运行。例如,在Sokoban规则{RWB=BRW RB=BR}的推理中,一组(红色)智能体会将(白色)箱子组织成指定的形状。
利用这些思想,我们构建了许多概率生成器,生成地牢、建筑、谜题和有趣的模拟。
附加资料:
- XML语法概述。
- 高分辨率截图和更多种子: ModernHouse, SeaVilla, Apartemazements, CarmaTower, Escheresque, PillarsOfEternity, Surface, Knots。
- 非官方技术笔记(Dan Ogles)和代码文档(Andrew Kay)。
马尔可夫算法
在字母表 A 上的马尔可夫算法是一个有序的规则列表。每条规则都是 x=y 的形式,其中 x 和 y 是 A 中的词,某些规则可能被标记为终止规则。将马尔可夫算法应用于单词 w 的过程如下:
- 找到第一条规则 x=y ,其中 x 是 w 的一个子串。如果没有这样的规则,则终止。
- 用 y 替换 w 中最左侧的 x。
- 如果找到的规则是终止规则,则终止。否则,转到步骤 1。
例如,考虑此字母表 {0, 1, x} 上的马尔可夫算法(ε 是空词):
1=0x
x0=0xx
0=ε
如果我们将其应用于字符串 110,我们会得到以下字符串序列:
110 -> 0x10 -> 0x0x0 -> 00xxx0 -> 00xx0xx -> 00x0xxxx -> 000xxxxxx -> 00xxxxxx -> 0xxxxxx -> xxxxxx
总的来说,该算法将数字的二进制表示转换为其单元表示。
马尔可夫的学生Vilnis Detlovs证明对于任何图灵机,都存在一个马尔可夫算法计算相同的函数。相比之下,语法是无序的重写规则集,L-系统是并行应用的重写规则。要了解更多有趣的马尔可夫算法示例,请查看马尔可夫的著作或在评论区中看到最大公约数示例,或参见维基百科上的乘法示例。
如何将马尔可夫算法推广到多维?首先,在多维中没有自然的方法将一个字符串插入到另一个字符串中,所以我们的重写规则的左右应该具有相同的大小。其次,没有自然的方法选择"最左边的"匹配。可能的选项有:
- 随机选择一个匹配项。这就是MJ的'(exists)'节点的做法。
- 选择所有匹配项。然而,这个选项存在问题,因为不同的匹配可能会重叠并产生冲突。可能的解决方案有:
- 贪婪地选择一个不相互冲突的最大子集。这就是MJ的'{forall}'节点的做法。
- 考虑所有匹配的叠加。也就是说,不是分离的值,而是在每个网格单元格保留波浪 - 布尔向量,告诉哪些时空模式是被禁止的,哪些是允许的。这就是MJ执行推理的方式。
我们失去了图灵完备性,因为我们的新过程不是确定性的,但实践表明,这种形式仍然允许描述大范围有趣的随机过程。
重写规则
最简单的MarkovJunior程序可能是(B=W)。它包含一条单一规则B=W。在每一次执行中,该程序将一个随机的黑色方块转换为白色方块。
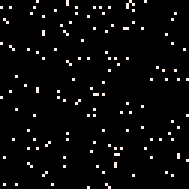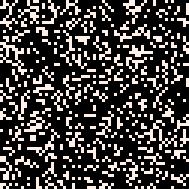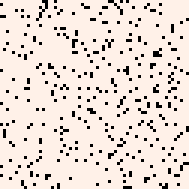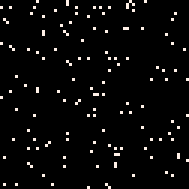
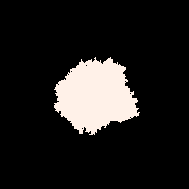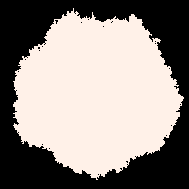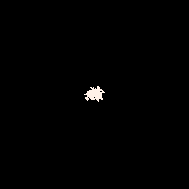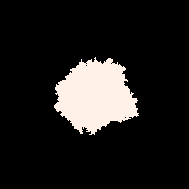


(B=W) | (WB=WW) | (WBB=WAW) | (WBB=WAW)
Growth模型(WB=WW)更有趣。在每一次执行中,它将相邻的黑白单元格对BW替换为白白单元格对WW。换句话说,在每一次执行中,它选择一个随机的黑色单元格,如果它相邻到一个白色单元格,就将其涂成白色。这个模型几乎与Eden生长模型相同:在每一次执行中,两个模型都选择相同集合中的黑色单元格。它们唯一的区别在于概率分布:一个是在相邻的黑白单元格对上的均匀分布,另一个是在黑色单元格上的均匀分布。
模型(WBB=WAW)以一行代码生成一个迷宫!将其与传统语言中的实现进行比较。任何MarkovJunior模型都可以在任意数量的维度上运行而不需要任何更改。在右侧,您可以看到MazeGrowth在3D中的最终结果,使用MagicaVoxel渲染。默认情况下,我们使用PICO-8调色板:



(RBB=WWR) | 删除环路的随机行走 | (RB=WR RW=WR)
我们可以把多条规则放在一个规则节点中。例如,(RBB=WWR RBW=GWP PWG=PBU UWW=BBU UWP=BBR)就是一种删除环路的随机行走。轨迹模型(RB=WR RW=WR)会生成不错的连通洞穴。
模型(RBB=WWR R*W=W*R)被称为Aldous-Broder迷宫生成算法。输入中的通配符符号*表示该方格可以是任意颜色。输出中的通配符表示该颜色在规则应用后不会改变。Aldous-Broder算法平均需要更多步骤来生成迷宫,但它有一个MazeGrowth没有的好特性:每个迷宫都有相同的概率被生成。换句话说,MazeTrail是一种无偏的迷宫生成算法,或者说它以均匀分布采样迷宫(或生成树)。Wilson算法是一种更高效的无偏迷宫生成算法。将其MarkovJunior实现[(models/Wilson.xml)]与常规语言的实现进行比较吧!
结合规则节点
我们可以把多个规则节点放在一个序列节点中,依次运行。在River模型中,我们首先构建一个随机Voronoi图,有2个源点,并将形成区域的边界作为河流的基础。然后我们生成一些额外的Voronoi种子来生长森林,同时从河流生长草地。最终我们得到了随机的河谷!
在Apartemazements中,我们从一个WFC节点开始,然后用规则节点进行构造性后处理:
- 准备约束条件:用单独的底色标记底部单元格,用单独的边界色标记其余的边界单元格(侧面和顶部)。边界单元格应映射到空,底部单元格应映射到除下之外的所有瓦片。
- 运行WFCPaths瓦片集生成封闭的楼梯环。
- 随机化光源。
- 从平面瓦片的角落删除列。
- 收缩双列、触地的列和触楼梯的列,但从转角瓦片生长的列除外。
- 在相邻的列之间生长窗户。
- 将窗户合并成更大的矩形。我们分几步进行:
- 检测窗户角触及窗户中点的不均匀模式。
- 标记这些模式并通过整个窗户边传播。
- 合并未标记的窗户边对。
- 将剩余的1x1窗户转换为墙。
结合节点的更有趣方式是将它们放入一个马尔可夫节点。马尔可夫节点大大扩展了我们的能力,因为它们允许返回到过去的节点。当一个马尔可夫节点处于活跃状态时,解释器会找到它的第一个匹配的子节点并应用它。在下一轮中,它会再次在列表中找到第一个匹配的节点,依此类推。马尔可夫节点使用的最简单例子是MazeBacktracker,在前面部分已经解释过了。
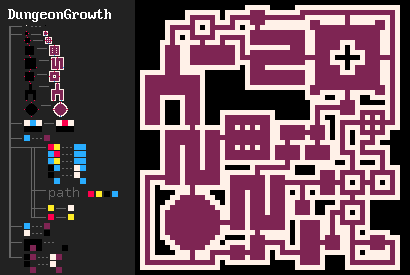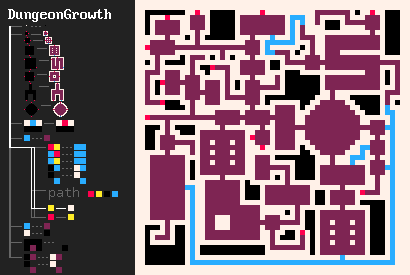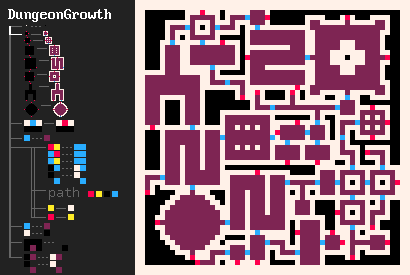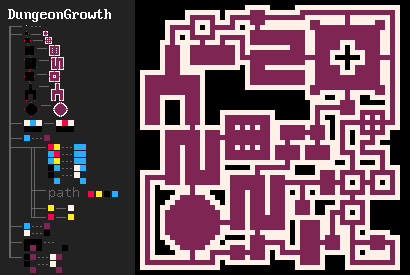
我最喜欢的例子之一,也是促使开发MarkovJunior的一个例子,是Bob Nystrom的地牢生成算法。它的步骤如下:
- 画一个网格
{PBB=**P}. - 生成一堆房间
(room.png). - 在剩余的网格上生成一个迷宫。我们可以使用任何迷宫生成算法,但MazeBacktracker是首选,因为它产生的分支点较少。
- 使生成的房间和走廊配置连通。这可以用一个马尔可夫节点优雅地实现
({GWW=**G}(GBW=*WG)). - 进行一些额外的连接
(GBG=*W* #5),使最终的地牢有循环。没有循环的地牢很无聊,因为玩家必须通过已经探索的区域返回。 - 收缩死胡同
{BBB/BWB=BBB/BBB}.
与REFAL一样,马尔可夫节点也可以嵌套:一旦进入子节点,我们就会忽略外部节点,直到子分支完成。
推理
MarkovJunior中的概率推理允许我们对未来状态施加约束,并只生成满足约束的运行。换句话说,推理将两个给定状态(或部分观察状态)用一系列重写规则连接起来。
使用推理的最简单例子是用路径连接两个点。在自回避行走模型(RBB=WWR)中,我们可以观察网格上的某个方格变为红色R。然后解释器只会生成导致该方格的行走。我们可以通过调节温度参数来更严格或更宽松地遵循目标。默认情况下,温度设置为0。
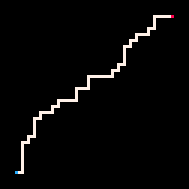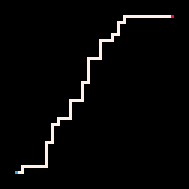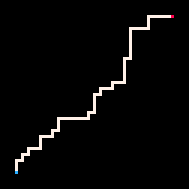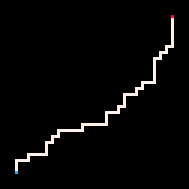
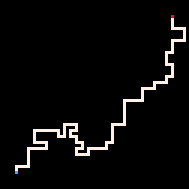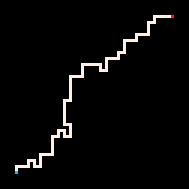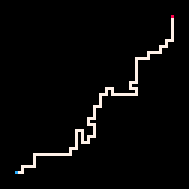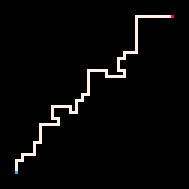
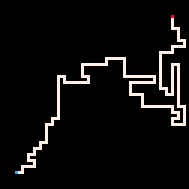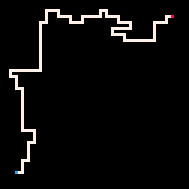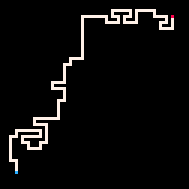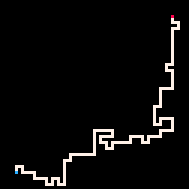

最冷 | 冷 | 热 | 最热
我们还可以观察所有奇数格子变为白色或红色。然后解释器会生成覆盖整个网格的自回避行走。
我们可以对任何重写规则进行推理。例如,对绘制楼梯规则进行推理可以连接两点并生成楼梯路径。对规则R**/**B=B**/**R进行推理会生成国际象棋马可以走的路径。在CrossCountry模型中的推理连接两点并考虑地形成本。对Sokoban规则集{RB=BR RWB=BRW}进行推理可以解决Sokoban谜题,甚至多智能体Sokoban谜题!

如果约束传播完成,这并不一定意味着目标状态是可实现的。但如果传播失败,我们就知道目标肯定是不可实现的。这使我们能够捕捉到在 Sokoban 中推箱子到错误的墙壁上,或者网格遍历路径将网格分成两个不连通部分的情况。除了这个布尔启发式外,我们也需要关注约束传播完成所需的最小步数。这个基于整数值的启发式是可接受的,我们在 A* 搜索中使用它来采样两个给定状态之间的重写规则路径。
开放问题
-
过程生成的程序合成。William Chyr 的演讲"Level Design in Impossible Geometry"并不是关于过程生成的,但我发现一张幻灯片非常能代表 pcg 实践。William 比较了他之前和后来的关卡设计方法。前者产生了混乱的关卡,而后者基于一个核心思想产生了更有结构、更有目的性的关卡。后来的关卡并不比之前简单,但更有记忆性,对玩家也更易感知。在我看来,左边的关卡就像是用过程生成的!它和我的过程体素拼图有着非常相似的感觉。我们能否制造出生成像右边那样关卡的生成器?这个问题似乎 AI 完备。但我认为它和经典的遗传编程问题,如 Koza 的割草机问题非常相似。例如,考虑一个简单的过程生成任务,就是在网格上生成 Hamiltonian 路径。即使对于像 29x29 这样小的网格尺寸,这个任务也是计算密集型的。但是,我们真的需要从所有可能的路径中采样吗?如果我们把这个任务交给一个人,他们可能会画一个螺旋形或者之字形曲线 - 这些设计比随机的 Hamiltonian 路径更有记忆性和目的性,而且可以推广到任意网格尺寸。总之,我们可以要求系统要么找到一条随机的 Hamiltonian 路径,要么找到一个生成 Hamiltonian 路径的短程序。在第一种情况下,结果会像幻灯片左边的关卡,在第二种情况下会像右边的关卡。解决后一个程序合成问题将创造出更有记忆性和目的性的生成器。
-
从样本合成模型。Markov 算法似乎是进行程序/模型合成的完美环境:没有变量、if 或 while,节点可以轻松移动而不破坏正确性,模型也很容易微分。随机 MJ 程序常常很有趣,能产生人性化的结果和行为。
- 我们能否从结果或一组结果合成一个 MJ 模型?
- 给定一个迷宫,是否可能确定(或给出概率)它是由MazeGrowth还是MazeBacktracker生成的?
- 通过推断 MarkovJunior 模型来解决抽象和推理挑战。反问题:利用 ARC 挑战的洞见构建一个更好的网格过程生成 DSL。
-
在波动空间运行的自定义算法。结合构造式和约束式过程生成的优点。相关:带有 Ising 能量或 ConvChain 能量等自定义能量函数的自定义算法(MJ 重写规则)。
-
概括模式的概念。
-
研究在其他(可能是非正则的)网格或任意图上的 MJ 类过程。
-
探索 Markov 算法的交互式扩展。可以将任何 MJ 模型转化为游戏,将特定的重写规则或节点分配给按键。
-
推进网格基础过程生成的前沿。ModernHouse还没有达到像Sims 2 的房屋这样人类设计房屋的结构多样性。使用更细微的约束。
评论
与图灵机和λ演算相比,Markov 算法可能是最简短、最简单的严格定义算法的方式。
练习:证明以下 Markov 算法可以找到用单元表示的两个数的最大公约数。例如,如果我们应用它到 111111*1111111111上,我们得到11。
1a=a1
1*1=a*
1*=*b
b=1
a=c
c=1
*=ε (halt)
快速模式匹配。MarkovJunior 解释器均匀地采样匹配,但它不会在每个回合扫描整个网格。为了保持模式匹配的快速,解释器记住之前找到的匹配,并只在被改变的地方进行搜索。当第一次遇到一个规则节点时,MJ 解释器使用Boyer-Moore 算法的多维版本。
随机放松。Markov 节点有一个很好的表示形式,它们是可微分节点的极限。考虑一个无序的重写规则集,每个规则 r 被赋予一个权重 w(r)。在每一步,解释器找到所有规则的所有匹配,并根据玻尔兹曼分布 p(r) ~ exp(-w(r)/t) 随机选择一个匹配。然后在冻结极限 t->0 下,我们得到一个由权重排序的 Markov 节点。这种构造的好处在于,对于任何 t>0 和一个典型的得分函数,多次运行的得分平均值将是权重的连续(对于实际应用来说也是平滑)函数。这意味着我们可以通过梯度下降找到最优权重,然后冻结系统以获得最终的离散程序。
请阅读Boris Kushner关于 A. A. Markov 及其构造数学工作的论文。
参考文献
主要参考文献:
- Andrey A. Markov, 算法理论, 1951。Markov 在 1947 年早期就用这些思想证明了半群中字词问题的算法不可判定性。另见后来的专著,有更详细的处理。我会感谢能找到英文公开获取的译本。
- Guilherme S. Tows, Imagegram, 2009。MarkovJunior 从 Imagegram 中取得了 forall 节点。
- Valentin Turchin, REFAL 语言, 1968。MJ 从 REFAL 中获取了嵌套 Markov 节点的思想。
- Brian Walker 等人, Dijkstra 映射的惊人威力, 2010。一个在 roguelike 社区中的讨论,包含了许多使用 Dijkstra 映射/距离域进行过程生成和 NPC AI 的技术。后续的文章:1,2。我们将 Dijkstra 映射泛化到任意重写规则。
- Pavlos S. Efraimidis, Paul Spirakis, 加权随机采样, 2005。
- 在自定义节点中使用的工作: 模型合成、波函数崩塌算法、ConvChain 算法。
- 经典算法: 约束传播、约束求解算法、图遍历、A* 搜索。
相关工作:
- Daniel Ritchie, 面向过程建模和设计的概率编程, 2016。
- Lingfeng Yang, 从执行跟踪到专门的推理, 2015。 源文本翻译如下:
示例来源:
- BasicKeys和Keys是Joris Dormans在Engineering Emergence: Applied Theory for Game Design中提出的图形语法的改编版本,2012年。这又发展自David Adams早期的工作Automatic Generation of Dungeons for Computer Games,2002年。我使用了这些模型的变体来生成SeaVilla中的钥匙-锁-桥拼图。
- CarmaTower是Antoine Lendrevie的一个体素场景的过程化版本。
- NystromDungeon模型是对Bob Nystrom地牢生成器的MarkovJunior移植版本。
- HamiltonianPath算法改编自此论文。可以将其与传统语言中的实现进行比较。
- DungeonGrowth中的房间形状取自r/proceduralgeneration帖子。需要注意的是,MJ解释器会自动执行该帖子中描述的优化。
- Wilson模型是对Wilson's algorithm的重写规则表达。可以将其与传统语言中的实现进行对比。
- MazeGrowth模型也被称为随机遍历的迷宫生成。可以将其与传统语言中的实现进行对比。
- Growth与Eden growth model密切相关。
- BernoulliPercolation是渗滤理论中广为研究的一个模型。
- NestedGrowth取自Imagegram。
- SmoothTrail改编自128_mhz的推特。
- SokobanLevel1似乎是Hiroyuki Imabayashi的Sokoban益智游戏的第一关。SokobanLevel2是Ionic Catalysts XI集合中的第452关。
- RainbowGrowth由mure在GitHub讨论中提出。
- MultiHeadedWalk、MultiHeadedDungeon和MultiHeadedWalkDungeon是基于Ilya Kudritsky的想法而创建的。
- Island模型由Guillaume Fiette开发。
- LostCity、Forest和Texture模型基于Andrew Kay的模型。
体素场景使用ephtracy开发的MagicaVoxel渲染。特别感谢Brian Bucklew向我展示了在roguelike关卡生成中Dijkstra场的威力,以及Kevin Chapelier给出的很多好的建议。GUI中使用的字体是Tamzen。
如何构建
MarkovJunior解释器是一个仅依赖于标准库的控制台应用程序。请下载.NET Core在Windows、Linux或macOS上运行:
dotnet run --configuration Release MarkovJunior.csproj
或者,下载并运行最新的发行版用于Windows。
生成的结果会放在output文件夹中。编辑models.xml来更改模型参数。使用MagicaVoxel打开.vox文件。
值得注意的移植、分支和衍生品
- Yuu制作了一个MarkovJunior的TypeScript版本,它在网页上运行,扩展了语言并添加了将节点绑定到按键的功能。
- Aseaday正在将MarkovJunior移植到JavaScript。
- Andrew Kay为C#源代码添加了XML文档。
- Dan Ogles编写了MarkovJunior技术笔记,重点关注字段和推理。
- Andrew Kay设计了MJr,这是一种基于模式重写的编译语言。
资金支持
MarkovJunior的开发得到了以下方的资助:

 Github
Github 文档
文档