Logo
Project Icon

sysidentpy

非线性系统识别和时序预测的Python工具库

SysIdentPyNARMAX模型系统识别时间序列预测非线性建模Github开源项目

SysIdentPy是一个开源Python库,专注于NARMAX模型及其变体的系统识别。该库提供先进的模型结构选择和参数估计技术,支持多种基函数,并可与神经网络和机器学习算法集成。它为时间序列分析和动态系统建模提供了灵活易用的框架,适用于构建动态非线性模型。

访问官网访问官网GithubGithub文档文档论文论文
介绍相关项目

DOI PyPI版本 许可证 未解决问题 已关闭问题 下载量 Python版本 状态 Discord 贡献者 星标

用于系统辨识和时间序列预测的NARMAX方法

从经典方法到神经网络

SysIdentPy提供最先进的技术来构建您的NARMAX模型，包括其变体NARX、NARMA、NAR、NFIR、ARMAX、ARX、ARMA等。它还包含大量有趣的示例，帮助您使用SysIdentPy构建非线性预测模型。

目录

简介

SysIdentPy是一个基于numpy构建的开源Python模块，用于使用NARMAX模型进行系统辨识，并在3-Clause BSD许可下分发。SysIdentPy为构建时间序列和动态系统的动态非线性模型提供了一个易于使用且灵活的框架。

使用SysIdentPy，您可以：

  • 构建和自定义非线性预测模型。
  • 使用最先进的技术进行模型结构选择和参数估计。
  • 尝试神经NARX模型和其他先进算法。

查看我们的文档！

如需深入了解，请查看我们的配套书籍：

非线性系统辨识

如何安装SysIdentPy？

安装SysIdentPy最简单的方法是使用pip

pip install sysidentpy

要求

SysIdentPy需要：

  • Python (>= 3.7)
  • NumPy (>= 1.9.2) 用于数值算法
  • Matplotlib >= 3.3.2 用于静态绘图和可视化
  • Pytorch (>=1.7.1) 用于构建NARX神经网络
  • scipy (>= 1.7.0) 用于数值和优化算法

该库兼容Linux、Windows和macOS。某些示例可能还需要额外的包，如pandas。

更多详情，请查看我们的安装指南

SysIdentPy的主要特性是什么？

特性这是什么？
NARMAX理念您可以构建NARMAX模型的变体，如NARX、NAR、NARMA、NFIR、ARMA、ARX、AR等。
模型结构选择易于使用的方法来选择构建模型的最佳项，包括FROLS和MetaMSS，以及与参数估计技术的多种组合来选择模型项。
基函数您可以使用不同的基函数来构建模型。您可以设置线性和非线性基函数，并将它们组合以获得自定义NARMAX模型。
参数估计超过15种方法来估计模型参数并测试不同的结构选择场景。
多目标参数估计您可以使用仿射信息来估计模型参数，最小化不同的目标函数。
模型仿真您可以使用SimulateNARMAX类轻松重现论文中的结果。此外，您可以使用不同的参数估计方法测试已发表的模型并比较性能。
神经NARX您可以使用SysIdentPy与Pytorch一起创建自定义神经NARX模型架构，支持Pytorch的所有优化器和损失函数。
通用估计器您可以使用来自scikit-learn、Catboost等包的估计器以及许多其他兼容接口和组合工具来创建NARMAX模型。

SysIdentPy 为何而生？

SysIdentPy 旨在成为一个免费开源的软件包，帮助社区为系统识别和时间序列预测设计 NARMAX 模型。更重要的是，它是目前最常用的 NARMAX 模型构建工具之一 —— Matlab 系统识别工具箱的免费且强大的替代品。

该项目由 Wilson R. L. Junior 积极维护，并正在寻找贡献者。

如何使用 SysIdentPy？

SysIdentPy 文档包含超过 20 个示例，帮助您入门：

  • 典型的"Hello World"示例，入门级介绍 SysIdentPy 的主要概念
  • 专门介绍 SysIdentPy 特性的章节，如模型结构选择算法、基函数、参数估计等
  • 专门介绍使用 SysIdentPy 处理真实世界数据集的用例章节。此外，还有与其他时间序列工具（如 Prophet、Neural Prophet、ARIMA 等）的简要比较和基准测试

示例

from torch import nn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sysidentpy.metrics import root_relative_squared_error
from sysidentpy.utils.generate_data import get_siso_data


# 生成模拟动态系统的数据集
x_train, x_valid, y_train, y_valid = get_siso_data(
  n=1000,
  colored_noise=False,
  sigma=0.001,
  train_percentage=80
)

使用 FROLS 算法构建多项式 NARX 模型

from sysidentpy.model_structure_selection import FROLS
from sysidentpy.basis_function import Polynomial
from sysidentpy.utils.display_results import results
from sysidentpy.utils.plotting import plot_residues_correlation, plot_results
from sysidentpy.residues.residues_correlation import compute_residues_autocorrelation
from sysidentpy.residues.residues_correlation import compute_cross_correlation

basis_function=Polynomial(degree=2)
model = FROLS(
  order_selection=True,
  n_info_values=10,
  extended_least_squares=False,
  ylag=2,
  xlag=2,
  info_criteria='aic',
  estimator='least_squares',
  basis_function=basis_function
)
model.fit(X=x_train, y=y_train)
yhat = model.predict(X=x_valid, y=y_valid)
rrse = root_relative_squared_error(y_valid, yhat)
print(rrse)
r = pd.DataFrame(
	results(
		model.final_model, model.theta, model.err,
		model.n_terms, err_precision=8, dtype='sci'
		),
	columns=['回归量', '参数', 'ERR'])
print(r)

回归量     参数        ERR
0        x1(k-2)     0.9000  0.95556574
1         y(k-1)     0.1999  0.04107943
2  x1(k-1)y(k-1)     0.1000  0.00335113

plot_results(y=y_valid, yhat=yhat, n=1000)
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="残差", ylabel="$e^2$")
x1e = compute_cross_correlation(y_valid, yhat, x2_val)
plot_residues_correlation(data=x1e, title="残差", ylabel="$x_1e$")

多项式

NARX 神经网络

from sysidentpy.neural_network import NARXNN
from sysidentpy.basis_function import Polynomial
from sysidentpy.utils.plotting import plot_residues_correlation, plot_results
from sysidentpy.residues.residues_correlation import compute_residues_autocorrelation
from sysidentpy.residues.residues_correlation import compute_cross_correlation

class NARX(nn.Module):
    def __init__(self):
        super().__init__()
        self.lin = nn.Linear(4, 10)
        self.lin2 = nn.Linear(10, 10)
        self.lin3 = nn.Linear(10, 1)
        self.tanh = nn.Tanh()

    def forward(self, xb):
        z = self.lin(xb)
        z = self.tanh(z)
        z = self.lin2(z)
        z = self.tanh(z)
        z = self.lin3(z)
        return z

basis_function=Polynomial(degree=1)

narx_net = NARXNN(
  net=NARX(),
  ylag=2,
  xlag=2,
  basis_function=basis_function,
  model_type="NARMAX",
  loss_func='mse_loss',
  optimizer='Adam',
  epochs=200,
  verbose=False,
  optim_params={'betas': (0.9, 0.999), 'eps': 1e-05} # 优化器的可选参数
)

narx_net.fit(X=x_train, y=y_train)
yhat = narx_net.predict(X=x_valid, y=y_valid)
plot_results(y=y_valid, yhat=yhat, n=1000)
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="残差", ylabel="$e^2$")
x1e = compute_cross_correlation(y_valid, yhat, x_valid)
plot_residues_correlation(data=x1e, title="残差", ylabel="$x_1e$")

神经网络

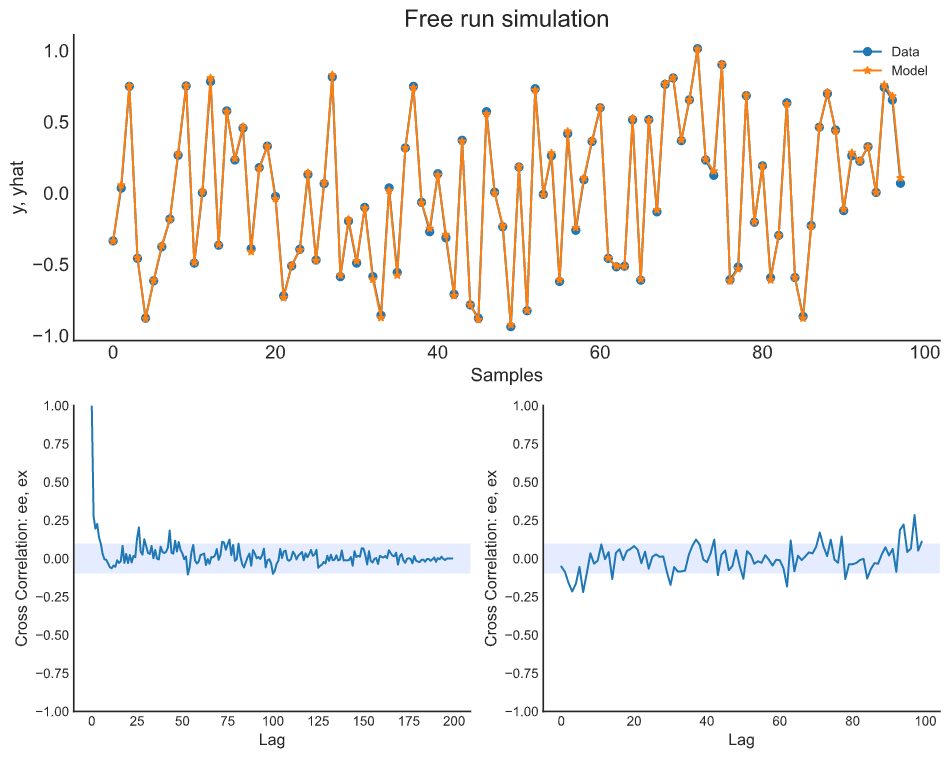
Catboost-narx

from catboost import CatBoostRegressor
from sysidentpy.general_estimators import NARX
from sysidentpy.basis_function import Polynomial
from sysidentpy.utils.plotting import plot_residues_correlation, plot_results
from sysidentpy.residues.residues_correlation import compute_residues_autocorrelation
from sysidentpy.residues.residues_correlation import compute_cross_correlation


basis_function=Polynomial(degree=1)
catboost_narx = NARX(
  base_estimator=CatBoostRegressor(
    iterations=300,
    learning_rate=0.1,
    depth=6),
  xlag=2,
  ylag=2,
  basis_function=basis_function,
  fit_params={'verbose': False}
)

catboost_narx.fit(X=x_train, y=y_train)
yhat = catboost_narx.predict(X=x_valid, y=y_valid)
plot_results(y=y_valid, yhat=yhat, n=1000)
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="残差", ylabel="$e^2$")
x1e = compute_cross_correlation(y_valid, yhat, x_valid)
plot_residues_correlation(data=x1e, title="残差", ylabel="$x_1e$")

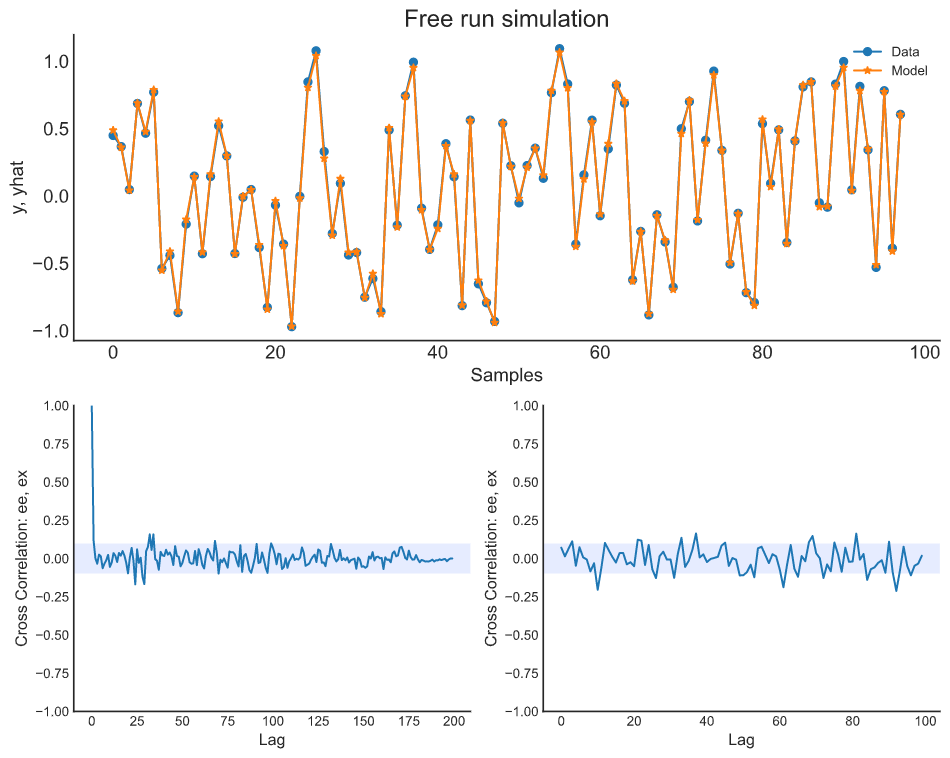
catboost

不使用NARX配置的Catboost

以下是不使用NARX配置的Catboost性能。


def plot_results_tmp(y_valid, yhat):
    _, ax = plt.subplots(figsize=(14, 8))
    ax.plot(y_valid[:200], label='数据', marker='o')
    ax.plot(yhat[:200], label='预测', marker='*')
    ax.set_xlabel("$n$", fontsize=18)
    ax.set_ylabel("$y[n]$", fontsize=18)
    ax.grid()
    ax.legend(fontsize=18)
    plt.show()

catboost = CatBoostRegressor(
  iterations=300,
  learning_rate=0.1,
  depth=6
)
catboost.fit(x_train, y_train, verbose=False)
plot_results_tmp(y_valid, catboost.predict(x_valid))

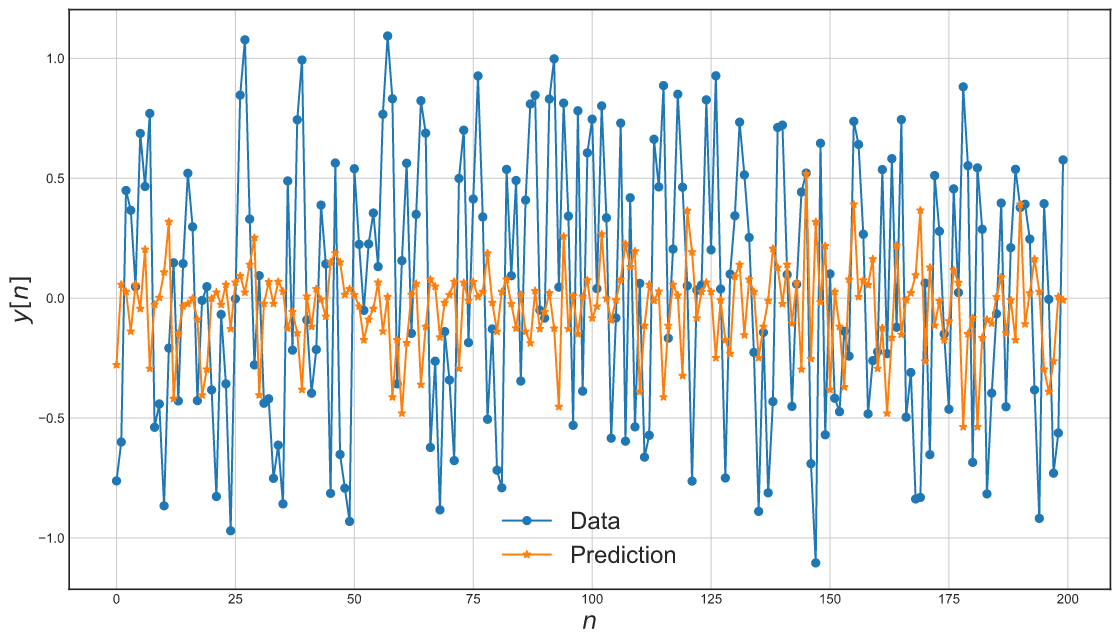
catboost

examples目录中有几个Jupyter笔记本，其中包含如何使用该软件包的教程以及sysidentpy的一些具体应用。试试看吧！

交流

引用

DOI

如果您在项目中使用了SysIdentPy，请给我发邮件。

如果您在科学出版物中使用了SysIdentPy，我们将感谢您引用以下论文：

  • Lacerda et al., (2020). SysIdentPy: A Python package for System Identification using NARMAX models. Journal of Open Source Software, 5(54), 2384, https://doi.org/10.21105/joss.02384
@article{Lacerda2020,
  doi = {10.21105/joss.02384},
  url = {https://doi.org/10.21105/joss.02384},
  year = {2020},
  publisher = {The Open Journal},
  volume = {5},
  number = {54},
  pages = {2384},
  author = {Wilson Rocha Lacerda Junior and Luan Pascoal Costa da Andrade and Samuel Carlos Pessoa Oliveira and Samir Angelo Milani Martins},
  title = {SysIdentPy: A Python package for System Identification using NARMAX models},
  journal = {Journal of Open Source Software}
}

灵感来源

文档和结构（甚至包括这一部分）公开地受到Scikit-learn、EinsteinPy和许多其他项目的启发，因为我们一直在使用它们来学习。

贡献者

赞助商

特别感谢我们的赞助商

黄金赞助商

Technium

月度赞助商

statisticallyinsifnificant

个人赞助商

Nath Keles
相关项目
项目侧边栏1项目侧边栏2
推荐项目
Project Cover

豆包MarsCode

豆包 MarsCode 是一款革命性的编程助手，通过AI技术提供代码补全、单测生成、代码解释和智能问答等功能，支持100+编程语言，与主流编辑器无缝集成，显著提升开发效率和代码质量。

Project Cover

AI写歌

Suno AI是一个革命性的AI音乐创作平台，能在短短30秒内帮助用户创作出一首完整的歌曲。无论是寻找创作灵感还是需要快速制作音乐，Suno AI都是音乐爱好者和专业人士的理想选择。

Project Cover

有言AI

有言平台提供一站式AIGC视频创作解决方案，通过智能技术简化视频制作流程。无论是企业宣传还是个人分享，有言都能帮助用户快速、轻松地制作出专业级别的视频内容。

Project Cover

Kimi

Kimi AI助手提供多语言对话支持，能够阅读和理解用户上传的文件内容，解析网页信息，并结合搜索结果为用户提供详尽的答案。无论是日常咨询还是专业问题，Kimi都能以友好、专业的方式提供帮助。

Project Cover

阿里绘蛙

绘蛙是阿里巴巴集团推出的革命性AI电商营销平台。利用尖端人工智能技术，为商家提供一键生成商品图和营销文案的服务，显著提升内容创作效率和营销效果。适用于淘宝、天猫等电商平台，让商品第一时间被种草。

Project Cover

吐司

探索Tensor.Art平台的独特AI模型，免费访问各种图像生成与AI训练工具，从Stable Diffusion等基础模型开始，轻松实现创新图像生成。体验前沿的AI技术，推动个人和企业的创新发展。

Project Cover

SubCat字幕猫

SubCat字幕猫APP是一款创新的视频播放器，它将改变您观看视频的方式！SubCat结合了先进的人工智能技术，为您提供即时视频字幕翻译，无论是本地视频还是网络流媒体，让您轻松享受各种语言的内容。

Project Cover

美间AI

美间AI创意设计平台，利用前沿AI技术，为设计师和营销人员提供一站式设计解决方案。从智能海报到3D效果图，再到文案生成，美间让创意设计更简单、更高效。

Project Cover

AIWritePaper论文写作

AIWritePaper论文写作是一站式AI论文写作辅助工具，简化了选题、文献检索至论文撰写的整个过程。通过简单设定，平台可快速生成高质量论文大纲和全文，配合图表、参考文献等一应俱全，同时提供开题报告和答辩PPT等增值服务，保障数据安全，有效提升写作效率和论文质量。

使用协议隐私政策广告服务
投诉举报邮箱: service@vectorlightyear.com
@2024 懂AI·鲁ICP备2024100362号-6·鲁公网安备37021002001498号