equiformer-pytorch - SE(3)/E(3)等变注意力网络的高效PyTorch实现

Equiformer - Pytorch（进行中）

这是Equiformer的实现，一个SE3/E3等变注意力网络，达到了新的最先进水平，并被EquiFold（Prescient Design）采用用于蛋白质折叠。

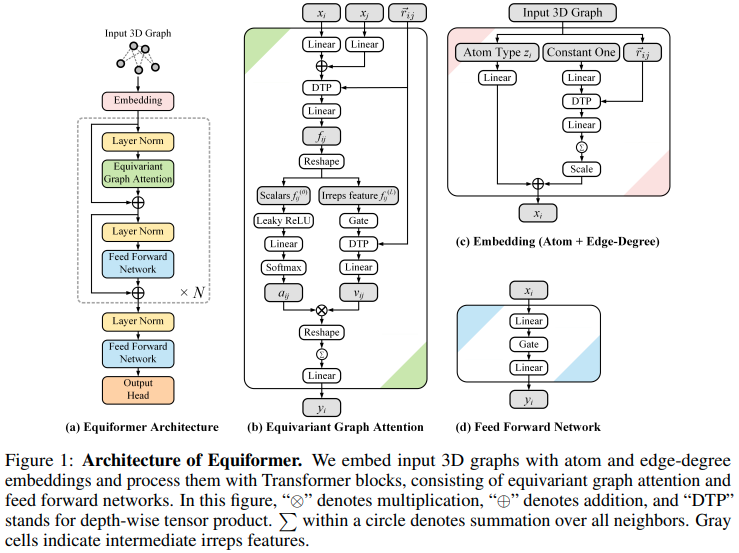
这个设计似乎是在SE3 Transformers的基础上构建的，将点积注意力替换为MLP注意力，并采用了GATv2中的非线性消息传递。它还进行了深度张量积以提高效率。如果您认为我有误解，请随时给我发邮件。

更新：最近有一项新的发展，使得SE3等变网络的度数扩展变得显著更好！这篇论文首先注意到，通过将表示对齐到z轴（或按其他惯例对齐到y轴），球谐函数变得稀疏。这从方程中消除了m_f维度。Passaro等人的后续论文指出Clebsch Gordan矩阵也变得稀疏，导致m_i和l_f的移除。他们还发现，将表示对齐到一个轴后，问题从SO(3)简化为SO(2)。Equiformer v2（官方仓库）在类transformer框架中利用这一点达到了新的最先进水平。

我肯定会在这方面投入更多的工作和探索。目前，我已经将前两篇论文中的技巧应用到Equiformer v1中，除了完全转换为SO(2)。

安装

$ pip install equiformer-pytorch

使用方法

import torch
from equiformer_pytorch import Equiformer

model = Equiformer(
    num_tokens = 24,
    dim = (4, 4, 2),               # 每种类型的维度，升序，长度必须与度数（num_degrees）匹配
    dim_head = (4, 4, 4),          # 每个注意力头的维度
    heads = (2, 2, 2),             # 注意力头的数量
    num_linear_attn_heads = 0,     # 全局线性注意力头的数量，可以看到所有邻居
    num_degrees = 3,               # 度数
    depth = 4,                     # 等变transformer的深度
    attend_self = True,            # 是否进行自注意力
    reduce_dim_out = True,         # 是否将输出维度降至1，例如用于预测类型1特征的新坐标
    l2_dist_attention = False      # 设为False以尝试MLP注意力
).cuda()

feats = torch.randint(0, 24, (1, 128)).cuda()
coors = torch.randn(1, 128, 3).cuda()
mask  = torch.ones(1, 128).bool().cuda()

out = model(feats, coors, mask) # (1, 128)

out.type0 # 不变类型0    - (1, 128)
out.type1 # 等变类型1  - (1, 128, 3)

这个仓库还包括一种使用可逆网络将内存使用与深度解耦的方法。换句话说，如果增加深度，内存成本将保持恒定，等于一个equiformer transformer块（注意力和前馈）的使用量。

import torch
from equiformer_pytorch import Equiformer

model = Equiformer(
    num_tokens = 24,
    dim = (4, 4, 2),
    dim_head = (4, 4, 4),
    heads = (2, 2, 2),
    num_degrees = 3,
    depth = 48,          # 深度为48 - 仅为展示它可以运行 - 实际上，在更高深度时似乎相当不稳定，所以架构仍需要更多工作
    reversible = True,   # 只需将此设为True以使用 https://arxiv.org/abs/1707.04585
).cuda()

feats = torch.randint(0, 24, (1, 128)).cuda()
coors = torch.randn(1, 128, 3).cuda()
mask  = torch.ones(1, 128).bool().cuda()

out = model(feats, coors, mask)

out.type0.sum().backward()

边

带有边的情况，例如原子键

import torch
from equiformer_pytorch import Equiformer
model = Equiformer(
    num_tokens = 28,
    dim = 64,
    num_edge_tokens = 4,       # 边类型数量，例如4种键类型
    edge_dim = 16,             # 边嵌入的维度
    depth = 2,
    input_degrees = 1,
    num_degrees = 3,
    reduce_dim_out = True
)

atoms = torch.randint(0, 28, (2, 32))
bonds = torch.randint(0, 4, (2, 32, 32))
coors = torch.randn(2, 32, 3)
mask  = torch.ones(2, 32).bool()

out = model(atoms, coors, mask, edges = bonds)

out.type0 # (2, 32)
out.type1 # (2, 32, 3)

使用邻接矩阵

import torch
from equiformer_pytorch import Equiformer

model = Equiformer(
    dim = 32,
    heads = 8,
    depth = 1,
    dim_head = 64,
    num_degrees = 2,
    valid_radius = 10,
    reduce_dim_out = True,
    attend_sparse_neighbors = True,  # 必须设置为true，此时它会断言你传入了邻接矩阵
    num_neighbors = 0,               # 如果设置为0，它将只考虑由邻接矩阵定义的连接邻居。但如果设置大于0的值，它将继续获取最近的点，直到达到这个数量，不包括邻接矩阵已经指定的点
    num_adj_degrees_embed = 2,       # 这将推导出二度连接并正确嵌入
    max_sparse_neighbors = 8         # 你可以限制邻居的数量，从邻接矩阵定义的稀疏邻居集合中采样，如果指定的话
)

feats = torch.randn(1, 128, 32)
coors = torch.randn(1, 128, 3)
mask  = torch.ones(1, 128).bool()

# 占位邻接矩阵
# 简单假设序列是一个长链(128, 128)

i = torch.arange(128)
adj_mat = (i[:, None] <= (i[None, :] + 1)) & (i[:, None] >= (i[None, :] - 1))

out = model(feats, coors, mask, adj_mat = adj_mat)

out.type0 # (1, 128)
out.type1 # (1, 128, 3)

致谢

- 感谢<a href="https://stability.ai/">StabilityAI</a>的慷慨赞助，以及我的其他赞助商

测试

等变性等测试

$ python setup.py test

示例

首先安装`sidechainnet`

$ pip install sidechainnet

然后运行蛋白质骨架去噪任务

$ python denoise.py

待办事项

- [x] 将xi和xj分离项目和求和逻辑移至Conv类
- [x] 将自交互键/值生成移至Conv，修复自交互卷积中无池化的问题
- [x] 采用朴素方法为DTP分割输入度的贡献
- [x] 对于高阶类型的点积注意力，尝试欧几里得距离
- [x] 考虑仅用于type0的全邻居注意力层，使用线性注意力

- [ ] 整合球面通道论文的新发现，followed by so(3) -> so(2)论文，将计算从O(L^6)降低到O(L^3)！
    - [x] 添加旋转矩阵 -> ZYZ欧拉角
    - [x] 用于推导r_ij -> (0, 1, 0)旋转矩阵的函数
    - [x] 准备get_basis以返回D，用于将表示旋转到(0, 1, 0)，大大简化球谐函数
    - [x] 添加批量旋转向量以与另一个对齐的测试 - 处理边缘情况(0, 0, 0)？
    - [x] 重做get_basis，只计算(0, 1, 0)的球谐函数Y并缓存
    - [x] 进行进一步优化以移除Clebsch-Gordan（因为m_i只依赖于m_o），如eSCN论文所述
    - [x] 验证是否可以在更高阶训练
    - [x] 弄清eSCN论文附录中的整个线性双射论点，以及为什么可以移除参数化lf
    - [x] 弄清为什么float32训练出现NaN
    - [ ] 重构为完整的so3 -> so2线性层，如eSCN论文所提议
    - [ ] 添加equiformer v2，并开始再次研究等变蛋白质骨架扩散

引用

@article{Liao2022EquiformerEG,
    title   = {Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs},
    author  = {Yi Liao and Tess E. Smidt},
    journal = {ArXiv},
    year    = {2022},
    volume  = {abs/2206.11990}
}
```bibtex
@article {Lee2022.10.07.511322,
    作者  = {李在贤 and Yadollahpour, Payman and Watkins, Andrew and Frey, Nathan C. and Leaver-Fay, Andrew and Ra, Stephen and 曹恭宏 and Gligorijevic, Vladimir and Regev, Aviv and Bonneau, Richard},
    标题   = {EquiFold: 使用新型粗粒度结构表示的蛋白质结构预测},
    定位号 = {2022.10.07.511322},
    年份    = {2022},
    doi     = {10.1101/2022.10.07.511322},
    出版社 = {冷泉港实验室},
    网址     = {https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322},
    电子预印本  = {https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322.full.pdf},
    期刊 = {bioRxiv}
}

@article{Shazeer2019FastTD,
    标题   = {快速Transformer解码：只需一个写入头},
    作者  = {Noam M. Shazeer},
    期刊 = {ArXiv},
    年份    = {2019},
    卷  = {abs/1911.02150}
}

@misc{ding2021cogview,
    标题   = {CogView: 通过Transformers掌握文本到图像生成},
    作者  = {丁明 and 杨卓艺 and 洪文毅 and 郑文迪 and 周畅 and 尹达 and 林俊阳 and 邹旭 and 邵周 and 杨红霞 and 唐杰},
    年份    = {2021},
    电子预印本  = {2105.13290},
    预印本库 = {arXiv},
    主要类别 = {cs.CV}
}

@inproceedings{Kim2020TheLC,
    标题   = {自注意力的Lipschitz常数},
    作者  = {Kim, Hyunjik and Papamakarios, George and Mnih, Andriy},
    会议名称 = {国际机器学习会议},
    年份    = {2020}
}

@article{Zitnick2022SphericalCF,
    标题   = {球面通道用于建模原子相互作用},
    作者  = {C. Lawrence Zitnick and Abhishek Das and Adeesh Kolluru and Janice Lan and Muhammed Shuaibi and Anuroop Sriram and Zachary W. Ulissi and Brandon C. Wood},
    期刊 = {ArXiv},
    年份    = {2022},
    卷  = {abs/2206.14331}
}

@article{Passaro2023ReducingSC,
  标题     = {将SO(3)卷积简化为SO(2)以实现高效的等变图神经网络},
  作者    = {Saro Passaro and C. Lawrence Zitnick},
  期刊   = {ArXiv},
  年份      = {2023},
  卷    = {abs/2302.03655}
}

@inproceedings{Gomez2017TheRR,
    标题   = {可逆残差网络：无需存储激活值的反向传播},
    作者  = {Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger Baker Grosse},
    会议名称 = {NIPS},
    年份    = {2017}
}

@article{Bondarenko2023QuantizableTR,
    标题   = {可量化的Transformers: 通过帮助注意力头不做任何事来去除异常值},
    作者  = {Yelysei Bondarenko and Markus Nagel and Tijmen Blankevoort},
    期刊 = {ArXiv},
    年份    = {2023},
    卷  = {abs/2306.12929},
    网址     = {https://api.semanticscholar.org/CorpusID:259224568}
}

@inproceedings{Arora2023ZoologyMA,
  标题   = {动物学：测量和改进高效语言模型的召回率},
  作者  = {Simran Arora and Sabri Eyuboglu and Aman Timalsina and Isys Johnson and Michael Poli and James Zou and Atri Rudra and Christopher R'e},
  年份    = {2023},
  网址     = {https://api.semanticscholar.org/CorpusID:266149332}
}