欢迎使用DYNAMAX!

测试状态

Dynamax是一个用JAX编写的概率状态空间模型(SSMs)库。它包含了各种SSMs的推断(状态估计)和学习(参数估计)代码，包括：

隐马尔可夫模型(HMMs)
线性高斯状态空间模型(又称线性动力系统)
非线性高斯状态空间模型
广义高斯状态空间模型(具有非高斯发射模型)

该库由一组核心的、功能纯粹的低级推断算法组成，以及一组提供更友好、面向对象接口的模型类组成。它与JAX生态系统中的其他库兼容，如optax(用于使用随机梯度下降估计参数)和Blackjax(用于使用哈密顿蒙特卡洛(HMC)或序贯蒙特卡洛(SMC)计算参数后验)。

文档

有关教程和API文档，请参见：https://probml.github.io/dynamax/。

对于支持结构化时间序列模型的dynamax扩展，请参见https://github.com/probml/sts-jax。

关于如何在bayeux中使用dynamax对SSM参数进行贝叶斯推断的示例，请参见https://jax-ml.github.io/bayeux/examples/dynamax_and_bayeux/。

安装和测试

要从PyPi安装最新版本的dynamax：

pip install dynamax                 # 安装dynamax和核心依赖项，或
pip install dynamax[notebooks]      # 安装演示笔记本依赖项

要安装最新的开发分支：

pip install git+https://github.com/probml/dynamax.git

最后，如果你是开发者，你可以安装dynamax及其测试和文档依赖项：

git clone git@github.com:probml/dynamax.git
cd dynamax
pip install -e '.[dev]'

运行测试：

pytest dynamax                         # 运行所有测试
pytest dynamax/hmm/inference_test.py   # 运行特定测试
pytest -k lgssm                        # 运行名称中包含lgssm的测试

什么是状态空间模型？

状态空间模型或SSM是一个部分观测的马尔可夫模型，其中隐藏状态$z_t$随时间按照马尔可夫过程演变，可能依赖于外部输入/控制/协变量$u_t$，并生成观测$y_t$。这在下面的图形模型中进行了说明。

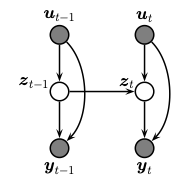
相应的联合分布具有以下形式(在dynamax中，我们仅关注离散时间系统)：

$$p(y_{1:T}, z_{1:T} | u_{1:T}) = p(z_1 | u_1) p(y_1 | z_1, u_1) \prod_{t=1}^T p(z_t | z_{t-1}, u_t) p(y_t | z_t, u_t)$$

这里$p(z_t | z_{t-1}, u_t)$被称为转移或动力学模型，$p(y_t | z_{t}, u_t)$被称为观测或发射模型。在这两种情况下，输入$u_t$是可选的；此外，观测模型可能具有自回归依赖性，在这种情况下我们写为$p(y_t | z_{t}, u_t, y_{1:t-1})$。

我们假设我们看到观测值$y_{1:T}$，并希望推断隐藏状态，可以使用在线滤波(即计算$p(z_t|y_{1:t})$)或离线平滑(即计算$p(z_t|y_{1:T})$)。我们可能还对预测未来状态$p(z_{t+h}|y_{1:t})$或未来观测$p(y_{t+h}|y_{1:t})$感兴趣，其中h是预测时间范围。(注意，通过使用隐藏状态来表示过去的观测，该模型可以具有"无限"记忆，不像标准的自回归模型。)所有这些计算都可以使用我们的库高效完成，我们将在下面讨论。此外，我们可以估计转移和发射模型的参数，我们也将在下面讨论。

更多信息可以在这些书籍中找到：

"机器学习：高级主题"，K. Murphy著，MIT出版社2023年。可在https://probml.github.io/pml-book/book2.html获得。

"贝叶斯滤波和平滑，第二版"，S. Särkkä和L. Svensson著，剑桥大学出版社，2023年。可在http://users.aalto.fi/~ssarkka/pub/bfs_book_2023_online.pdf获得。

使用示例

Dynamax包含许多种SSM的类。你可以使用这些模型来模拟数据，并可以使用标准学习算法如期望最大化(EM)和随机梯度下降(SGD)来拟合模型。下面我们演示了高斯发射的HMM的高级(面向对象)API。(有关此代码的可运行版本，请参见此笔记本。)

import jax.numpy as jnp
import jax.random as jr
import matplotlib.pyplot as plt
from dynamax.hidden_markov_model import GaussianHMM

key1, key2, key3 = jr.split(jr.PRNGKey(0), 3)
num_states = 3
emission_dim = 2
num_timesteps = 1000

# 创建高斯HMM并从中采样数据
hmm = GaussianHMM(num_states, emission_dim)
true_params, _ = hmm.initialize(key1)
true_states, emissions = hmm.sample(true_params, key2, num_timesteps)

# 创建新的高斯HMM并用EM拟合
params, props = hmm.initialize(key3, method="kmeans", emissions=emissions)
params, lls = hmm.fit_em(params, props, emissions, num_iters=20)

# 绘制EM迭代过程中的边际对数概率
plt.plot(lls)
plt.xlabel("EM迭代次数")
plt.ylabel("边际对数概率")

# 使用拟合模型进行后验推断
post = hmm.smoother(params, emissions)
print(post.smoothed_probs.shape) # (1000, 3)

JAX允许你使用vmap轻松地向量化这些操作。例如，你可以如下所示对一批发射进行采样和拟合。

from functools import partial
from jax import vmap

num_seq = 200
batch_true_states, batch_emissions = \
    vmap(partial(hmm.sample, true_params, num_timesteps=num_timesteps))(
        jr.split(key2, num_seq))
print(batch_true_states.shape, batch_emissions.shape) # (200,1000) 和 (200,1000,2)

# 创建新的高斯HMM并用EM拟合
params, props = hmm.initialize(key3, method="kmeans", emissions=batch_emissions)
params, lls = hmm.fit_em(params, props, batch_emissions, num_iters=20)

这些示例展示了dynamax模型，但我们也可以直接调用低级推断代码。

贡献

有关如何贡献的详细信息，请参见此页面。

关于

核心团队：Peter Chang, Giles Harper-Donnelly, Aleyna Kara, Xinglong Li, Scott Linderman, Kevin Murphy。

其他贡献者：Adrien Corenflos, Elizabeth DuPre, Gerardo Duran-Martin, Colin Schlager, Libby Zhang和其他此处列出的人。

MIT许可证。2022年