计算几何Unity库

这个库包含两个文件夹。一个用于测试目的,另一个文件夹是您拖入项目中的文件夹。

确保所有输入坐标都归一化到0-1范围,以避免浮点精度问题!有一个"Normalizer"对象可以帮助您进行归一化和反归一化。这并不总是必需的,但如果您发现算法不起作用,请尝试对输入坐标进行归一化。

其中一些算法以教程形式提供,地址如下:https://www.habrador.com/tutorials/math/ 和 https://www.habrador.com/tutorials/interpolation/

代码已使用Unity 2018.4 LTS进行测试,但应该适用于其他版本。

1. 相交
2. 生成网格
3. 凸包
4. 三角剖分
5. Voronoi图
6. 多边形裁剪
7. 沿曲线挤出网格
8. 变形网格
9. 其他
10. 待办事项
11. 主要更新

1. 相交

1.1 二维空间(部分也在三维空间中实现)

点-三角形

点-多边形 存在浮点精度问题

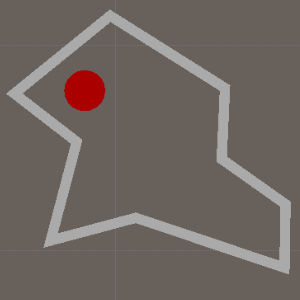
三角形-三角形

AABB-AABB

线-线

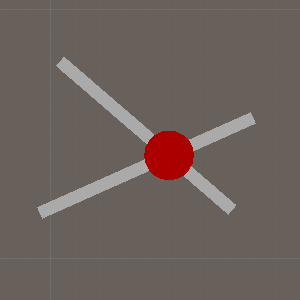
射线-平面

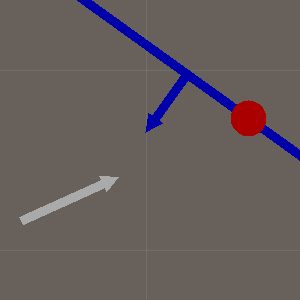
线-平面

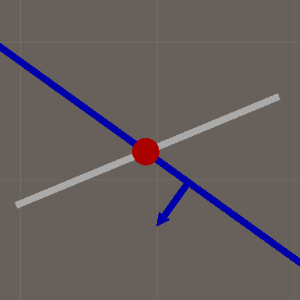
平面-平面

点-圆

2. 生成网格

网格网格

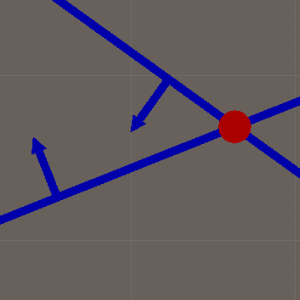
网格形状: 箭头、圆、线

3. 凸包

计算几何中的一个常见问题是找到一组点的凸包。

二维空间

Jarvis March算法 也称为"礼物包装"算法

这是最简单的算法。思路是:

1. 找到凸包上的一个点(可以是x坐标最小的点)
2. 要找到凸包上的下一个点,随机选择一个点,然后测试所有其他点,看其他点是否在凸包上最后一个点和随机选择的点之间的右侧。如果是,则这个点是更好的点。继续这样做,直到找不到更右侧的点。最后这个点也在凸包上。

这个算法可能很慢,但它很稳健,可以轻松处理共线点。有时使用一个易于理解的算法比使用更复杂的算法更好。

此算法的可视化可以在这里找到:https://www.youtube.com/watch?v=Z_wcJUgvohc

Quickhull算法

Valve的Dirk Gregorious写的"Implementing Quickhull"是一篇关于这个算法的好文章。它有图片,所以你可以看到发生了什么。但思路是:

1. 找到三个在凸包上的点形成的第一个三角形。现在你可以删除这个三角形内的所有点
2. 对于每条边(你从三角形的三条边开始),找到这条边"外部"的点
3. 对于每条边(并使用你知道在这条边外部的点),找到离这条边最远的点。这个点也在凸包上。现在原始三角形的边被分成了两条。删除原始边和两条新边形成的新三角形内的所有点。
4. 对每条新边重复步骤2和3

三维空间

迭代算法 与Quickhull非常相似。

1. 像二维Quickhull一样,你从找到一个三角形开始。但这是三维的,所以你必须找到另一个点以获得四面体。
2. 逐个添加所有其他点。如果点在目前的凸包内,忽略它。否则,你必须检查哪些三角形从该点可见,并删除它们。然后从刚刚删除的三角形的边界到新点构建三角形。

此算法的可视化可以在这里找到:https://www.youtube.com/watch?v=Yv2OhCV1BpU

4. 三角剖分

4.1 凸多边形三角剖分

你有一个凸包上的点集需要进行三角剖分。如果存在共线点（在同一直线上的点），你有四个选择：

1. 忽略共线点，对凸包进行三角剖分。覆盖的面积将保持不变。
2. 对凸包进行三角剖分，然后通过分割三角形边来添加共线点。
3. 在凸包内部添加一个点。
4. 使用下面称为"可见边算法的点集三角剖分"的算法。

4.2 凹多边形三角剖分

耳切法

目前只能处理孔洞，不能处理孔中孔。但它有优化措施以获得更好看的三角剖分。耳切算法借鉴了Delaunay三角剖分的思想，以获得更美观的三角形。因此，如果你遇到这个算法的问题（由于某些边界情况），你可以尝试约束Delaunay算法 - 它们应该给出相同的结果。我认为约束Delaunay更稳健，因为你不必用不可见的接缝连接孔洞。

这个算法的可视化演示可以在这里找到：https://www.youtube.com/watch?v=mw8aLh_lPoo

4.3 点集三角剖分

"可见边算法"的点集三角剖分

对于想要进行三角剖分的点集，你可以按以下步骤操作：

1. 对所有点按x方向然后y方向排序
2. 找到第一个三角形
3. 逐个添加剩余的排序点，并在现有三角剖分的可见边上构建三角形。要确定一条边是否从该点可见，你需要从现有三角形构建凸形状。然后对凸包中的每条边，与该点构建一个三角形。如果这个三角形是顺时针方向的，则该边是可见的，你可以添加一个新的三角形。

这个算法的可视化演示可以在这里找到：https://www.youtube.com/watch?v=MkMXKu1m6A4

"逐点"算法的点集三角剖分

对于想要进行三角剖分的点集，你可以按以下步骤操作：

1. 生成所有点的凸包。
2. 使用上面提到的几种算法之一对凸包进行三角剖分。
3. 逐个添加剩余的点，通过将它们所在的三角形分割成三个新的三角形。

4.4 Delaunay三角剖分

"增量"法

你在所有要进行三角剖分的点周围生成一个大三角形。然后逐个添加每个点。点所在的三角形被分割成三个新的三角形。分割后，通过翻转边来恢复Delaunay三角剖分。当所有点都添加完毕后，移除第一个大三角形的残余部分。这种方法也被称为Bowyer–Watson算法。这个算法的可视化演示可以在这里找到：https://www.youtube.com/watch?v=YNQR5tH-s40

"翻转边"法

你使用一种"不好"的三角剖分方法（在这种情况下，可以是上面提到的"可见边"或"逐点"方法）对点进行三角剖分。然后遍历所有边，检查是否应该翻转边以形成更好的三角形。当没有更多的边可以翻转时，你就完成了！这个算法的可视化演示可以在这里找到：https://www.youtube.com/watch?v=-d7Nb4fxL5s 和 https://www.youtube.com/watch?v=lR_SzgEkDwk

约束三角剖分

你将约束添加到点集中，并使用上述方法之一生成Delaunay三角剖分。使用这个三角剖分来找出哪些边与约束相交。然后翻转这些边，直到它们不再与约束相交。最后移除"在约束内部"的三角形。它可以处理多个孔洞和单个外壳，但不能处理孔中孔。如果你真的需要孔中孔，你可以总是运行算法两次，然后合并输出。类似的算法是耳切法三角剖分，但我认为这种方法更稳健。这个算法的可视化演示可以在这里找到：https://www.youtube.com/watch?v=Z-1ExrWMTfA

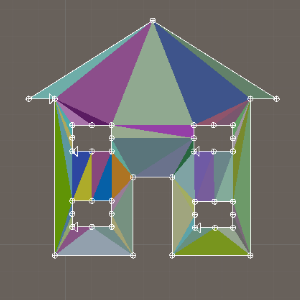
4.2 行进算法

行进方块：

对2D网格中的点进行三角剖分。

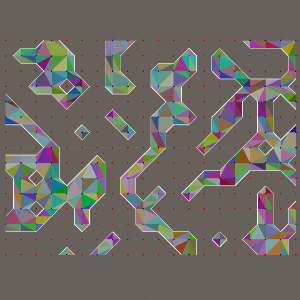
元圆：

元圆类似于元球，但在2D中。使用行进方块算法。

5. Voronoi图

从Delaunay三角剖分生成

你首先使用某种方法生成Delaunay三角剖分。然后利用从Delaunay三角剖分可以得到Voronoi图的事实。对于每个Delaunay三角形，你生成一个圆，使三角形的顶点位于圆的边缘。这个圆的中心是属于该三角形的Voronoi图面的一个角点。

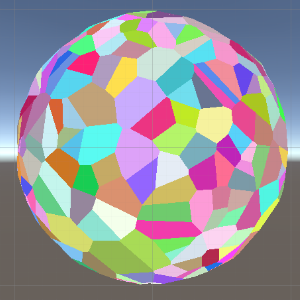
从球面上的Delaunay三角剖分生成

要获得球面上点的Delaunay三角剖分，你只需生成这些点的凸包。要在3D空间中生成Voronoi图，过程与2D空间相同 - 只是你需要在3D空间中找到给定圆边缘上三个点的圆心。

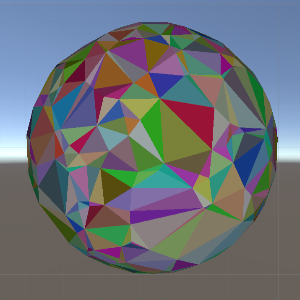
该算法的可视化演示可以在此处找到：https://www.youtube.com/watch?v=xAVL4qz_2AE

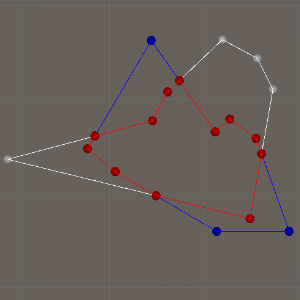
6. 多边形裁剪

Greiner-Hormann方法

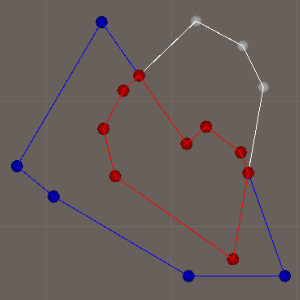
Sutherland-Hodgman方法

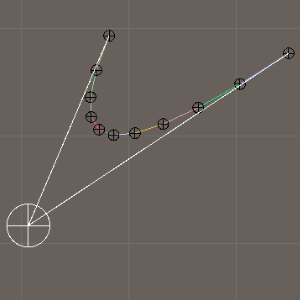
7. 沿曲线挤出网格

Catmull-Rom样条

贝塞尔曲线

• 线性

• 二次

• 三次

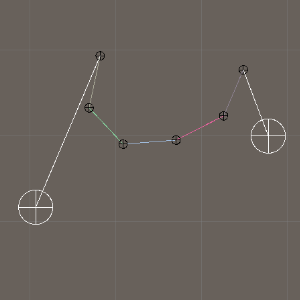
曲线操作

• 将曲线分割成等步长的方法

• 沿曲线挤出网格的方法。这里的难点是在曲线上的某一点找到一个方向，包括以下方法：

  • 固定向上
  • 弗莱纳法向（也称为弗莱纳框架）
  • 旋转最小化框架（也称为平行传输框架或毕肖普框架）

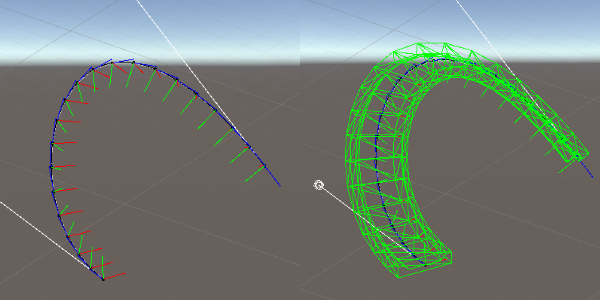
8. 变形网格

计算几何中最有趣的部分！

用平面切割网格（待完成）

如果新网格不连接，则会分离网格，因此切割后可能会得到两个以上的网格。

简化网格

将生成一个与原始网格相似但三角形更少的网格。用于生成LOD等。实现了以下算法：

• 使用二次误差度量（QEM）的迭代配对收缩。这是最常见的网格简化算法。该算法的可视化演示可以在此处找到：https://www.youtube.com/watch?v=biLY19kuGOs

9. 其他

三角形是否按顺时针方向排列？

点是在向量的左侧、上面还是右侧？

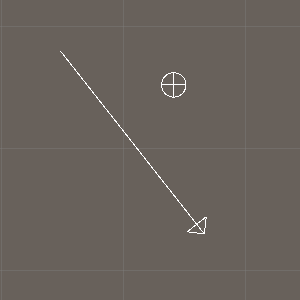
**点是在平面的左侧、上面还是右侧？**这与到平面的距离相同。

四边形是否为凸形？

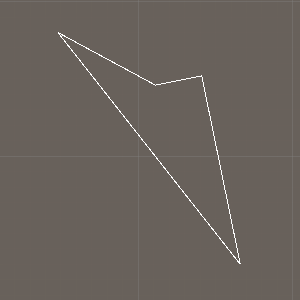
点是否在同一直线上的两点之间？

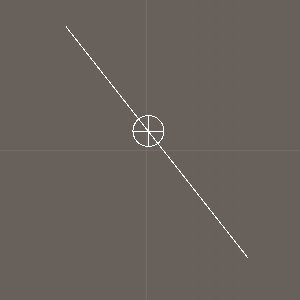
线段上的最近点？

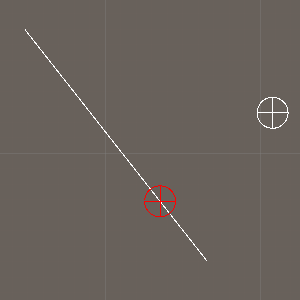
是否已经通过某点？

如果我们从A点到B点，如何知道我们是否已经通过B点？仅测量到B点的距离，并说如果我们距离B点小于x米就算通过，这种方法不够准确！

待办事项

需要实现的内容

• 2D凸包：
  • Graham扫描法
  • 迭代法
  • 分治法
• 3D凸包：
  • 分治法
  • 快速凸包算法
• 2D凹包：
  • Alpha形状
• 三角剖分：
  • 行进立方体
  • 动态约束Delaunay三角剖分
  • 使用行进立方体的元球体
  • 在三角剖分而不是网格上的行进正方形
  • 通过"水平分解为梯形"的多边形三角剖分
  • 生成无限Delaunay三角剖分的方法（用于地形等）
• 变形网格：
  • 网格贴花
  • 碰撞后变形网格，如车祸
  • 复制Twitter上的算法，可以拍摄世界的照片，然后将几何体放置在照片中任何想要的位置（https://twitter.com/mattstark256）
• Voronoi图：
  • Fortune算法
  • 逐点法
  • 从3D空间中的一组点生成
• 使用SAT的凸多边形-多边形相交
• 不规则网格（Oskar Stålberg风格）

待修复事项

• 制作一个测试场景，以测试"通过三角剖分步进法找出点所在的三角形"是否正常工作
• Delaunay算法中的"翻转边"可能在共线点上存在问题
• 移除或澄清2D和3D之间的转换
• 带有嵌套孔洞的耳切法
• 修复点在多边形内的浮点精度问题（参见《计算机图形学几何工具》）。这也可用于改进耳切法，因为使用了相同的思路
• 耳切法应使用半边数据结构，这样更易于翻转三角形，且更加标准化
• 在约束Delaunay三角剖分中，有一种更快的方法来找出哪些边与约束相交

主要更新

2020年12月

• 添加了用平面切割网格的功能
• 添加了使用迭代算法的3D凸包（与快速凸包算法非常相似）
• 添加了球面上的3D Voronoi图和Delaunay三角剖分
• 添加了使用"基于二次误差度量(QEM)的迭代对收缩"进行网格简化

2020年11月

• 添加了移动立方体算法
• 添加了元圆算法
• 添加了沿曲线挤出网格的功能
• 添加了耳切法三角剖分

2020年3月

• 添加了插值方法，如贝塞尔曲线和Catmull-Rom样条

社交媒体

• 访问我的作品集

• 在Twitter上关注我