llama2.c 傻瓜教程

目的

本仓库对 llama2.c 中的推理文件进行逐行详细解析。内容非常详尽，适合初学者阅读。

你需要对 Transformer 架构有一定了解。如果你是完全的新手，请先参考这篇excellent 博客。

前提知识

Transformer 架构:3个组成部分
1. 嵌入层(1次矩阵乘法)
2. 层:Q、K、V、O 和前馈网络权重 W1、W2 和 W3 的矩阵乘法(7次矩阵乘法)
3. 分类器:在我们的例子中,分类器只是 (vocab,768) x (768,1) 的矩阵乘法。基本上是给出每个下一个词元的概率。(1次矩阵乘法)

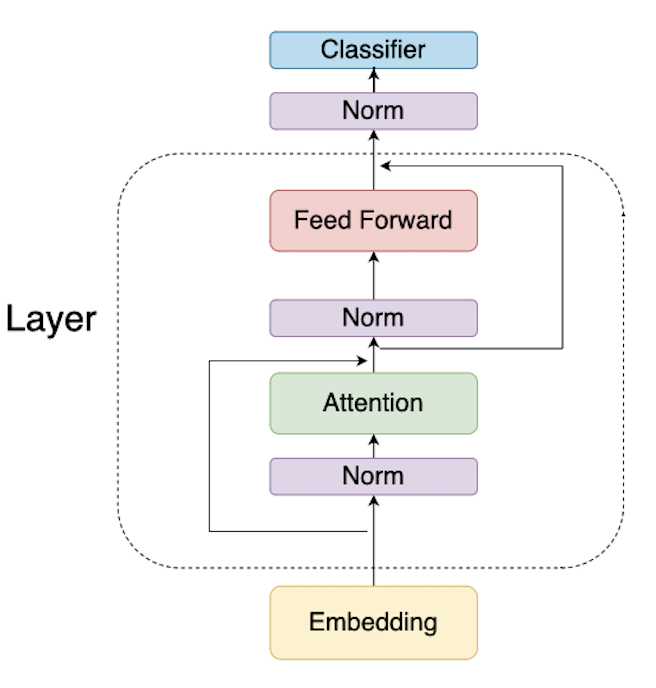
代码解析

代码分为3个部分:结构体、函数和 main() 中的读取逻辑。我们将首先看结构体,然后进入 main(),最后介绍重要的函数。

注意:代码取自提交 4e23ad83。原始仓库可能因为新的提交而有所不同。 但 99% 的逻辑应该保持不变 :)

第一部分:结构体

我们定义了3个结构体,用于存储模型配置、模型权重和前向传播过程中的中间值(运行状态)

Config 结构体:定义 transformer 模型。
1. n_layers, vocab_size:层数(例如 llama-2 有 32 层/BERT-base 有 12 层)和词汇表中的词元数量(英语通常是 30k)
2. dim 和 hidden_dim:定义 Q、K、V 和 O 的形状 (dim,dim),以及 W1、W2 (dim, hidden_dim) 和 W3 (hidden_dim, dim)
3. n_heads:查询(Q)的头数。如果 n_heads=12,则矩阵 Q=(768,768) 的行为/视为 (768, 768/12,768)
4. n_kv_heads:K 和 V 的头数。为什么这些与上面不同?:阅读多查询论文
5. seq_len:我们将生成的词元数量

typedef struct {
    int dim; // transformer 维度
    int hidden_dim; // 用于前馈网络层
    int n_layers; // 层数
    int n_heads; // 查询头数
    int n_kv_heads; // 键/值头数(可以 < 查询头数,因为多查询)
    int vocab_size; // 词汇表大小,通常为 256(字节级)
    int seq_len; // 最大序列长度
} Config;

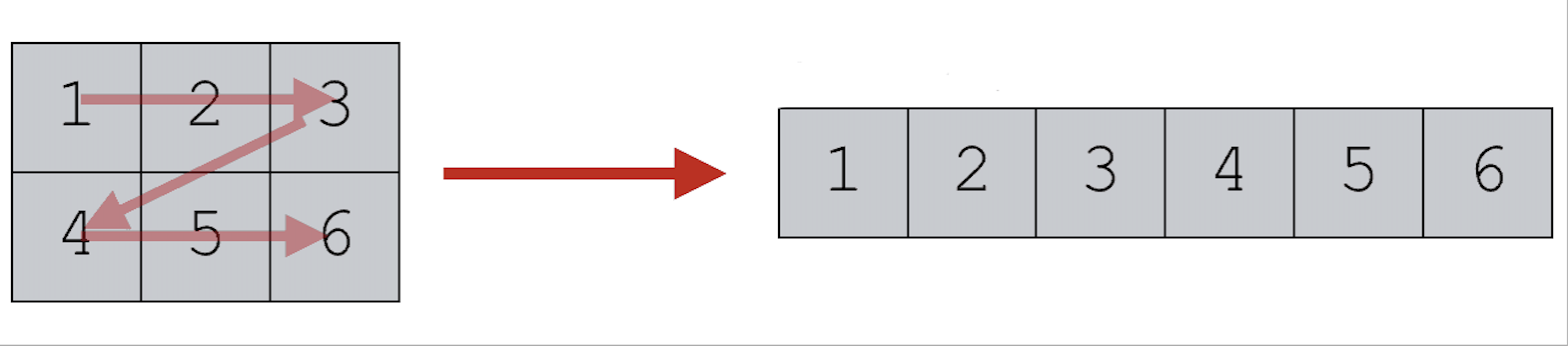
llama 的 Weight 结构体。这是我们 PyTorch 中 ffn=nn.Linear(...) 的对应部分。
1. 为什么它们是 float*?因为所有矩阵都只是一维展平数组。见下图
2. 代码是自解释的,并附有形状注释。rms_ 是用于归一化的权重,freq_cis_ 用于 RoPE 嵌入。我们稍后会详细介绍 RoPE。
3. wcls 是最终的分类器。大小为 (vocab, dim) 的矩阵,将最终嵌入从向量映射到词汇表中每个词元的概率。

typedef struct {
    // 词元嵌入表
    float* token_embedding_table;    // (vocab_size, dim)
    // rmsnorms 的权重
    float* rms_att_weight; // (layer, dim) rmsnorm 权重
    float* rms_ffn_weight; // (layer, dim)
    // 矩阵乘法的权重
    float* wq; // (layer, dim, dim)
    float* wk; // (layer, dim, dim)
    float* wv; // (layer, dim, dim)
    float* wo; // (layer, dim, dim)
    // 前馈网络的权重
    float* w1; // (layer, hidden_dim, dim)
    float* w2; // (layer, dim, hidden_dim)
    float* w3; // (layer, hidden_dim, dim)
    // 最终的 rmsnorm
    float* rms_final_weight; // (dim,)
    // RoPE 相对位置嵌入的 freq_cis
    float* freq_cis_real; // (seq_len, dim/2)
    float* freq_cis_imag; // (seq_len, dim/2)
    // (可选)最后一层的 logits 分类器权重
    float* wcls;
} TransformerWeights;

中间激活(运行状态)
1. 在前向传播过程中,我们需要存储中间值,例如矩阵乘法的输出或归一化后的输出。稍后我们将查看所有变量
2. key_cache 和 value_cache 存储先前词元的 key 和 value 输出。例如,在生成第 5 个词元时,这将存储前 4 个词元的 key 和 value。

typedef struct {
    // 当前激活波
    float *x; // 当前时间戳的激活 (维度,)
    float *xb; // 相同，但在残差分支内 (维度,)
    float *xb2; // 仅为方便而设的额外缓冲区 (维度,)
    float *hb; // 前馈网络中隐藏维度的缓冲区 (隐藏维度,)
    float *hb2; // 前馈网络中隐藏维度的缓冲区 (隐藏维度,)
    float *q; // 查询 (维度,)
    float *k; // 键 (维度,)
    float *v; // 值 (维度,)
    float *att; // 分数/注意力值的缓冲区 (注意力头数, 序列长度)
    float *logits; // 输出logits
    // kv缓存
    float* key_cache;   // (层数, 序列长度, 维度)
    float* value_cache; // (层数, 序列长度, 维度)
} RunState;

我们将在遇到函数时进行查看。现在让我们看看 main() 内的逻辑

第2部分：Main（如果你只对前向传播逻辑感兴趣，可以跳过这部分）

获取命令行参数。没什么特别的。目前你可以通过以下方式调用 run.c：
1. ./run llama2_7b.bin
2. ./run llama2_7b.bin 0.1 -> 带温度参数
3. ./run llama2_7b.bin 0.1 100 -> 带温度参数和步数（生成的输出token数）
最后声明 config 和 weights

int main(int argc, char *argv[]) {
    // 简易C语言参数解析
    char *checkpoint = NULL;  // 例如 out/model.bin
    float temperature = 0.9f; // 例如 1.0 或 0.0
    int steps = 256;          // 运行的最大步数，0：使用seq_len
    // 'checkpoint' 是必要参数
    if (argc < 2) {
        printf("用法: %s <checkpoint文件> [温度] [步数]\n", argv[0]);
        return 1;
    }
    if (argc >= 2) {
        checkpoint = argv[1];
    }
    if (argc >= 3) {
        // 可选温度。0.0 = （确定性）argmax采样。1.0 = 基准
        temperature = atof(argv[2]);
    }
    if (argc >= 4) {
        steps = atoi(argv[3]);
    }
    // 用时间作为随机数种子。如果你想要确定性行为，使用温度0.0
    srand((unsigned int)time(NULL)); 
    // 读取model.bin文件
    Config config;
    TransformerWeights weights;

读取 checkpoint 文件。
1. 如果你熟悉PyTorch，通常 config.json 和 model.bin 是分开的（我们像字典一样加载权重）。但这里 train.py 以特定格式将所有内容保存在一个 .bin 文件中。这种特定格式使我们能够轻松地先读取配置，然后逐一读取每个权重。

详细信息

shared_weights：输入嵌入矩阵和输出分类器矩阵是否应该相同？
接下来加载到 weights。通过 file_size = ftell(file); 获取文件大小。与普通PyTorch推理不同，我们不将所有权重加载到RAM中。相反，我们在需要时懒加载，调用 mmap(..) 来分配RAM内存。更多详情请阅读
最后调用 checkpoint_init_weights（下面是函数片段）。这里我们将权重指针映射到 mmap 返回的正确地址。由于我们已经读取了配置，我们在 float* weights_ptr = data + sizeof(Config)/sizeof(float); 这行中为其偏移。

void checkpoint_init_weights(TransformerWeights *w, Config* p, float* f, int shared_weights){
float* ptr = f;
w->token_embedding_table = ptr;
ptr += p->vocab_size * p->dim;
w->rms_att_weight = ptr;
.......
}

上述部分讨论的原始代码

    int fd = 0;
    float* data = NULL;
    long file_size;
    {
        FILE *file = fopen(checkpoint, "rb");
        if (!file) {
            printf("无法打开检查点文件 %s！\n", checkpoint);
            return 1;
        } 
        // 读取配置头
        if(fread(&config, sizeof(Config), 1, file) != 1) { return 1; }
        // 负的词汇表大小是表示非共享权重的一种取巧方式。有点奇怪。
        int shared_weights = config.vocab_size > 0 ? 1 : 0;
        config.vocab_size = abs(config.vocab_size);
        // 确定文件大小
        fseek(file, 0, SEEK_END); // 将文件指针移到文件末尾
        file_size = ftell(file); // 获取文件大小，以字节为单位
        fclose(file);
        
        // 将Transformer权重内存映射到data指针
        fd = open(checkpoint, O_RDONLY); // 以只读模式打开
        if (fd == -1) { printf("打开失败！\n"); return 1; }
        data = mmap(NULL, file_size, PROT_READ, MAP_PRIVATE, fd, 0);
        if (data == MAP_FAILED) { printf("mmap失败！\n"); return 1; }
        float* weights_ptr = data + sizeof(Config)/sizeof(float);
        checkpoint_init_weights(&weights, &config, weights_ptr, shared_weights);
    }

读取词汇文件 -> 大部分直接明了，只有几个细节
1. vocab 是 char** 类型，因为每个标记都是一个字符串，而 vocab 是标记列表。
2. 通过 vocab_size 进行循环，读取每个标记

// 目前我们无法运行超过 config.seq_len 步骤
    if (steps <= 0 || steps > config.seq_len) { steps = config.seq_len; }
    // 读取 tokenizer.bin 文件
    char** vocab = (char**)malloc(config.vocab_size * sizeof(char*));
    {
        FILE *file = fopen("tokenizer.bin", "rb");
        if (!file) {
            printf("无法打开分词器文件 tokenizer.bin！运行 "
            "python tokenizer.py 将 tokenizer.model 转换为 tokenizer.bin\n");
            return 1;
        }
        int len;
        for (int i = 0; i < config.vocab_size; i++) {
            if(fread(&len, sizeof(int), 1, file) != 1) { return 1; }
            vocab[i] = (char *)malloc(len + 1);
            if(fread(vocab[i], len, 1, file) != 1) { return 1; }
            vocab[i][len] = '\0'; // 添加字符串结束符
        }
        fclose(file);
    }

main 中的前向循环和采样（跳转到重要部分）

为运行状态/中间值分配内存。我们传入模型的第一个 token 是 BOS 标记（"语句开始"），其词汇索引为 1。

    RunState state;
    malloc_run_state(&state, &config);
    
    // 当前位置
    long start = time_in_ms();
    int next;
    int token = 1; // 1 = Llama-2 sentencepiece 中的 BOS 标记
    int pos = 0;
    printf("<s>\n"); // 显式打印初始 BOS 标记（=1），在风格上对称

前向循环：
1. transformer(token, pos, &config, &state, &weights); 将每个标记作为序列中下一个标记的分类器得分存储在 state.logits 中。（transformer 函数的内容将在下一节介绍）
2. 接下来我们进行采样。为什么需要采样以及如何进行？
  - 假设你想让 AI 完成电影对话，你的输入是 "卢克，我是你的" 。现在 llama 给出每个标记作为下一个词的得分。例如，假设我们的标记是 ["苹果", "足球", "父亲", "兄弟"]，llama 给它们的得分是 [0.3, 0.1, 0.9, 0.7]。现在要选择下一个标记，我们可以选择最高分（得分为 0.9 的 "父亲"），或者我们以与得分成比例的概率对标记进行采样，这样我们可以在预测中获得更多的多样性（在当今世界非常重要😁）。
3. 让我们讨论更多细节：如果 temperature=0，那就是最大采样。对于 temperate>0，我们使用 softmax 将 state.logits 转换为概率，并存回 state.logits。sample(..) 函数从 state.logits 概率分布中采样返回一个标记。在这里阅读更多内容
4. 生成的标记 next 成为下一个输入标记，在 token=next 这一行。

while (pos < steps) {
        // 前向传递 transformer 以获取下一个标记的 logits
        transformer(token, pos, &config, &state, &weights);
        // 采样下一个标记
        if(temperature == 0.0f) {
            // 贪婪最大值采样
            next = argmax(state.logits, config.vocab_size);
        } else {
            // 对 logits 应用温度
            for (int q=0; q<config.vocab_size; q++) { state.logits[q] /= temperature; }
            // 对 logits 应用 softmax 以获取下一个标记的概率
            softmax(state.logits, config.vocab_size);
            // 现在我们要从这个分布中采样以获取下一个标记
            next = sample(state.logits, config.vocab_size);
        }
        printf("%s", vocab[next]);
        fflush(stdout);

        // 前进
        token = next;
        pos++;
    }

实际前向传递

从 main() 调用的 transformer(token, pos, &config, &state, &weights); 的详细信息

以下部分大量使用 2d/3d 数组索引。我们在这里简要介绍，以使生活更轻松

如果矩阵 float* mat 的大小为 (dim1, dim2, dim3)，那么访问 mat[l][i][j] 的指针是 dim2*dim3*l + dim3*i + j; - 这是 公式-1，我们稍后会经常引用。如果你感到困惑，请阅读链接

如何从头的角度看待矩阵？

K（键）float* wk 是一个形状为 (layer, dim, dim) 的矩阵，从头的角度来看是 (layer, dim, n_heads, head_dim)
便利变量。除了使用memcpy将token的嵌入复制到s->xb中，没有什么特别之处。为什么不直接使用float* content_row？因为s->xb将会发生变化，而使用content_row会改变模型权重。

void transformer(int token, int pos, Config* p, RunState* s, TransformerWeights* w) {
    // 一些便利变量
    float *x = s->x;
    int dim = p->dim;                  
    int hidden_dim =  p->hidden_dim;  
    int head_size = dim / p->n_heads; 
    float* content_row = &(w->token_embedding_table[token * dim]);
    // 将token嵌入复制到x中
    memcpy(x, content_row, dim*sizeof(*x));

RoPE：旋转位置嵌入

公式：通过在2D平面上旋转来变换特征对。例如，如果你的向量是[0.8, 0.5, -0.1, 0.3]，我们将它们分组成对：[[0.8,-0.1], [0.5, 0.3]，然后旋转某个角度$\theta$。这个$\theta$从一开始就是固定的（不可学习）。在论文中，$\theta_{i}$的值是$10000^{2(i-1)/d}$。

RoPE公式（对于分组成对的2个特征）如下。$m$是对的索引。$\theta$是我们从.bin文件加载的固定参数。

$$ \left[ {\begin{array}{ccccc} x_{m}^{i} & x_{m}^{j} \ \end{array} } \right] * \left[ {\begin{array}{ccccc} cos(m\theta_{m}) & -sin(m\theta_{m}) \ sin(m\theta_{m}) & cos(m\theta_{m}) \ \end{array} } \right] $$

我们的示例对[[0.8,-0.1], [0.5, 0.3]将被如下转换。请记住，对于第一对[0.8, 0.1]，$m=0$（因此$sin(0)=0$）。对于第二对，$m=1$。

$$ \left[ {\begin{array}{ccccc} 0.8 & -0.1 \ \end{array} } \right] * \left[ {\begin{array}{ccccc} 1 * 1 & -0.0 * 1 \ 0.0 * 1 & 1.0 * 1 \ \end{array} } \right] = \left[ {\begin{array}{ccccc} 0.8 & -0.1 \ \end{array} } \right] $$

$$ \left[ {\begin{array}{ccccc} 0.5 & 0.3 \ \end{array} } \right] * \left[ {\begin{array}{ccccc} 0.86 * 1 & -0.5 * 1 \ 0.5 * 1 & 0.86 * 1 \ \end{array} } \right] = \left[ {\begin{array}{ccccc} 0.58 & 0.08 \ \end{array} } \right] $$

将两者结合，输出为[[0.8, 0.1], [0.58, 0.08]]，现在解对它们将得到[0.8, 0.58, 0.1, 0.08]。所以RoPE将[0.8, 0.5, -0.1, 0.3]转换为[0.8, 0.58, -0.1, 0.08]。请记住，如果特征的dim=768，那么有一半的384个$\theta$。

回到代码

我们获取当前位置的$\theta$（pos是我们的$m$）。freq_cis_real_row是$cos(m\theta)$，freq_cis_imag_row是$sin(m\theta)$。

    // 提取freq_cis_real和freq_cis_imag的"pos"行
    float* freq_cis_real_row = w->freq_cis_real + pos * head_size / 2;
    float* freq_cis_imag_row = w->freq_cis_imag + pos * head_size / 2;

遍历层。对层的输入应用rmsnorm。rmsnorm函数计算如下：

out\; = \;  (x*g*n)/\sum_{i} \sqrt{x_{i}^{2}}

其中$x$是输入，$g$是可学习参数（下面的w->rms_attn_weight），$n$是dim。 matmul对2D矩阵和1D矩阵进行矩阵乘法。即(A, B) x (A,)。其实现非常简单（我们将在最后讨论）。我们将Q、K、V与s->xb（rmsnorm的输出）相乘，并将结果存储在s->q、s->k等中。

for(int l = 0; l < p->n_layers; l++) {
// 注意力层的rmsnorm
    rmsnorm(s->xb, x, w->rms_att_weight + l*dim, dim);
    
    // 对当前位置进行qkv矩阵乘法
    matmul(s->q, s->xb, w->wq + l*dim*dim, dim, dim);
    matmul(s->k, s->xb, w->wk + l*dim*dim, dim, dim);
    matmul(s->v, s->xb, w->wv + l*dim*dim, dim, dim);

对每个注意力头应用我们之前讨论的2维cos/sin变换到s->q和s->k。我们对每个头分别进行处理，因此取h*head_size的偏移量。

// 对每个注意力头的q和k向量应用RoPE旋转
        for (int h = 0; h < p->n_heads; h++) {
            // 获取此注意力头的q和k向量
            float* q = s->q + h * head_size;
            float* k = s->k + h * head_size;
            // 使用freq_cis_real和freq_cis_imag旋转q和k
            for (int i = 0; i < head_size; i+=2) {
                float q0 = q[i];
                float q1 = q[i+1];
                float k0 = k[i];
                float k1 = k[i+1];
                float fcr = freq_cis_real_row[i/2];
                float fci = freq_cis_imag_row[i/2];
                q[i]   = q0 * fcr - q1 * fci;
                q[i+1] = q0 * fci + q1 * fcr;
                k[i]   = k0 * fcr - k1 * fci;
                k[i+1] = k0 * fci + k1 * fcr;
            }
        }

一旦我们获得当前标记的q、k、v，我们需要计算自注意力。这里我们将查询乘以键。k和v仅用于当前标记。我们将所有过去标记的k、v存储在key_cache_row和value_cache_row中。
- 例如，如果我们到目前为止已经生成了标记（"fox"、"jumps"、"over"），那么我们已经在缓存中存储了之前前向传播中"fox"和"jumps"的Q和V。我们不需要重新计算。
- 由于缓存存储所有层和所有标记（最大标记数为seq_length）的键和查询，其维度为(layer, seq_length, dim)。seq_length通常被称为context。
考虑上述示例中的以下代码。假设seq_length=32（这意味着我们最多生成32个标记）。pos=2，因为"fox"是第3个标记（Python从0开始索引，所以是第2个）。
- 我们已经在s->key_cache中填充了layer*(pos-1)*dim个值。在进行自注意力之前，我们还需要将当前标记"fox"的键和值填入s->key_cache。这就是memcpy(key_cache_row, s->k, dim*sizeof(*key_cache_row));所做的事。

// 将此时间步（pos）的键值保存到我们的kv缓存中
int loff = l * p->seq_len * dim; // 为方便起见，计算kv缓存层偏移量
float* key_cache_row = s->key_cache + loff + pos * dim;
float* value_cache_row = s->value_cache + loff + pos * dim;
memcpy(key_cache_row, s->k, dim*sizeof(*key_cache_row));
memcpy(value_cache_row, s->v, dim*sizeof(*value_cache_row));

执行自注意力

公式

\begin{align} 
out = (QK^{T})\;V/\sqrt{d} \\
其中\;\;\; Q=(1,dim) \;\; K=(dim,N) \;\; V=(dim,N)
\end{align}

上述公式中的$N$是pos（生成文本的当前长度）如果你记住 s->q、s->k 在头部维度上的形状为 (dim, n_heads, head_dim)，而 key_cache 的形状为 (seq_length, n_heads, head_dim)，这部分代码就变得很简单了。让我们逐步分析代码：

int h 是当前的头计数。让我们逐行看：
1. q = s->q + h*head_size：获取第 h 个头的起始指针。记住公式1。矩阵大小为 (dim, n_heads, head_dim)，我们需要 s->q[0][h][0]，即 0*n_heads*head_dim + h*head_dim + 0，也就是 h*head_size。
2. att = s->att + h * p->seq_len：我们将注意力存储在运行状态变量 s->attn 中。
3. 对于每个位置（如果回到"fox"、"jumps"、"over"的例子，pos 当前是2）
  1. 要获取第 l 层、第 t 位置和第 h 个头，我们做 s->key_cache + l*seq_length*dim + t*n_heads*head_dim + h*head_dim。由于之前定义的 loff 已经是 l*seq_length*dim，最终偏移量是 loff + t*n_heads*head_dim + h*head_size。因为 n_heads*head_dim=dim，所以我们得到偏移量 loff + t*dim + h*head_size。

现在我们有了 q (head_size,)、k (head_size,) 和 att (seq_length,)。我们可以计算第 h 个头在位置 t 的自注意力分数。我们对所有头和到目前为止的所有位置进行求和。

上面得到的 attn 形状为 (seq_length, )。接下来我们将其与形状为 (seq_length, dim) 的 v 相乘。记住，下面的循环是在上一节开始的 for (h = 0; h < p->n_heads; h++) 内部。

前馈网络和分类器

要完成注意力模块，我们需要与 O 相乘，这在第一行完成。下一行 accum 添加来自跳跃连接（红色箭头）的输入和注意力的输出。然后进行归一化。
接下来我们计算 FFN 输出，公式为：

out = W_3 * σ(W_1X * W_2X)

其中 σ 是 silu 激活函数。这部分是不言自明的

// 现在对于PyTorch中的FFN，我们有：self.w2(F.silu(self.w1(x)) * self.w3(x))
// 首先计算self.w1(x)和self.w3(x)
matmul(s->hb, s->xb, w->w1 + l*dim*hidden_dim, dim, hidden_dim);
matmul(s->hb2, s->xb, w->w3 + l*dim*hidden_dim, dim, hidden_dim);
// F.silu; silu(x)=x*σ(x)，其中σ(x)是logistic sigmoid函数
for (int i = 0; i < hidden_dim; i++) {
	s->hb[i] = s->hb[i] * (1.0f / (1.0f + expf(-s->hb[i])));
}
// 与w3(x)进行元素级乘法
for (int i = 0; i < hidden_dim; i++) {
	s->hb[i] = s->hb[i] * s->hb2[i];
}
// 最后的矩阵乘法得到ffn的输出
//memcpy(tmp_w_hid, w->w2 + l*dim*hidden_dim, hidden_dim*dim*sizeof(float));
matmul(s->xb, s->hb, w->w2 + l*dim*hidden_dim, hidden_dim, dim);

最后一行是另一个累加（上图中的第二个跳跃层）

accum(x, s->xb, dim);

最终分类器

在对所有层运行上述模块后，我们得到一个形状为(dim,)的嵌入。我们需要将其转换为形状为(vocab,)的向量，其中每个条目告诉我们该词作为下一个标记的得分是多少。

在与分类器矩阵（w->wcls）相乘之前，我们对嵌入进行归一化。得分保存在s->logits中

// 最终rmsnorm
rmsnorm(x, x, w->rms_final_weight, dim);
// 分类器得到logits
matmul(s->logits, x, w->wcls, p->dim, p->vocab_size);

结束

一旦我们得到s->logits，我们就对下一个标记进行采样（重复此操作直到获得seq_length个标记）。这在"主函数中的前向循环和采样"部分已经介绍过了。恭喜！现在你知道LLM是如何工作的，以及如何用C语言编写它们。如果你现在想知道如何用Python编写它们，请参考modelling_llama.py

这是一张猫的图片 :)