$\Phi$-SO : 物理符号优化

物理符号优化（$\Phi$-SO）-一个为物理学构建的符号优化包。

源码：WassimTenachi/PhySO
文档：physo.readthedocs.io

亮点

$\Phi$-SO的符号回归模块使用深度强化学习来推断符合数据点的解析物理定律，在函数形式的空间中搜索。

physo能够利用：

• 物理单位约束，通过维度分析减少搜索空间（[Tenachi et al 2023]）

• 类约束，搜索单一解析函数形式，准确适应多个数据集——每个数据集都由其独特的拟合参数集所控制（[Tenachi et al 2024]）

$\Phi$-SO恢复阻尼谐振子的方程：

https://github.com/WassimTenachi/PhySO/assets/63928316/655b0eea-70ba-4975-8a80-00553a6e2786

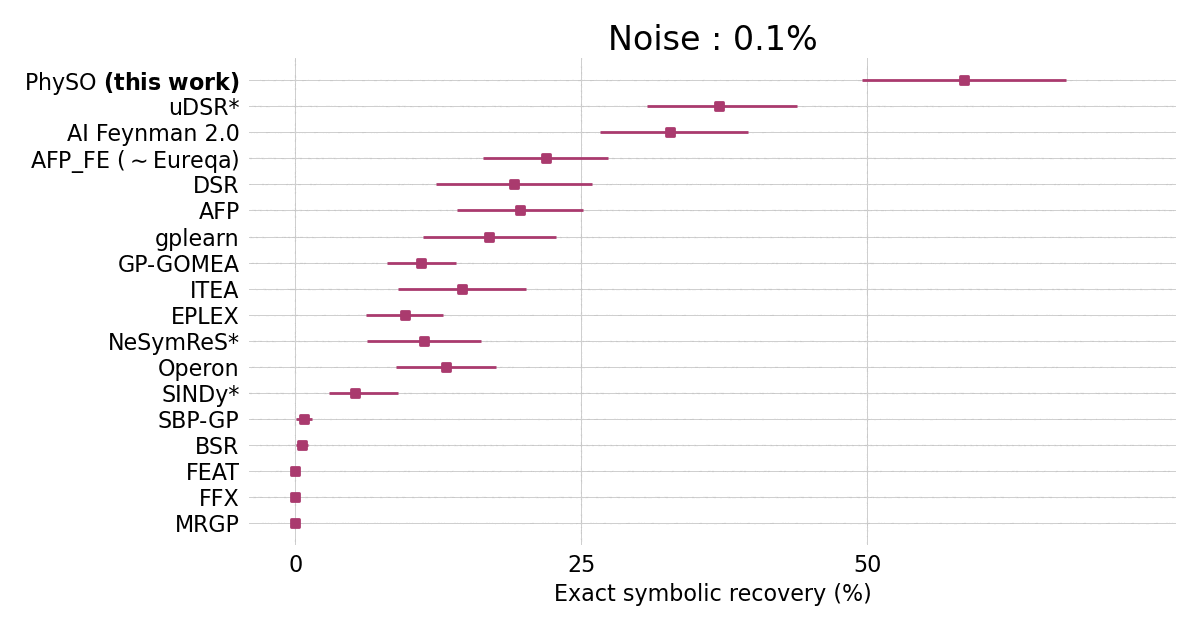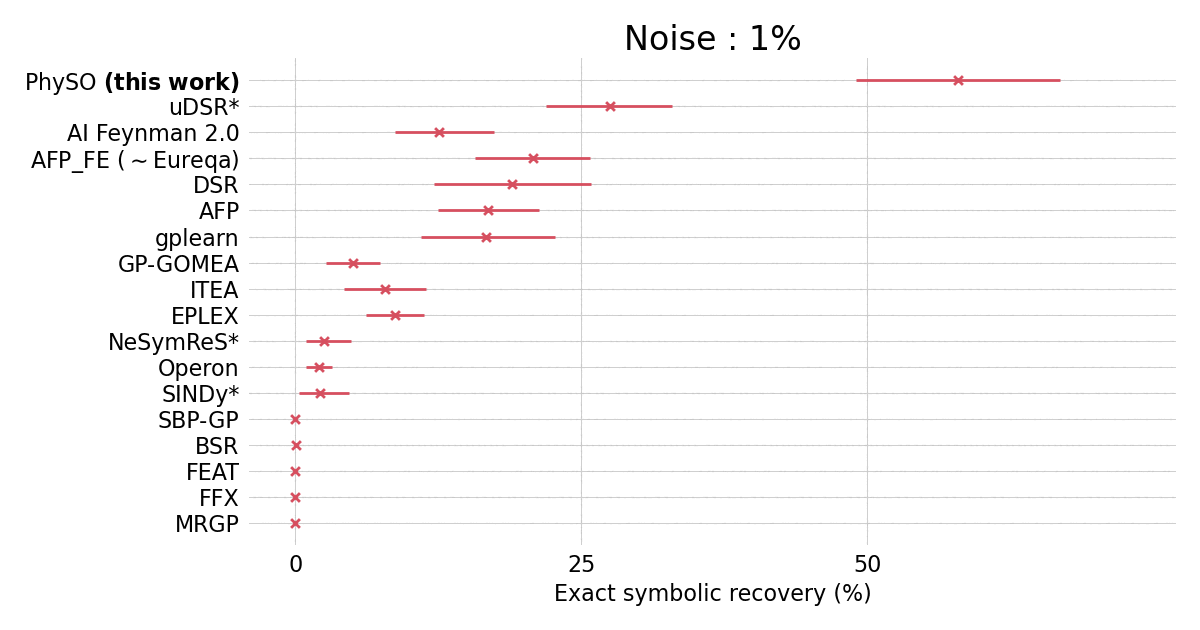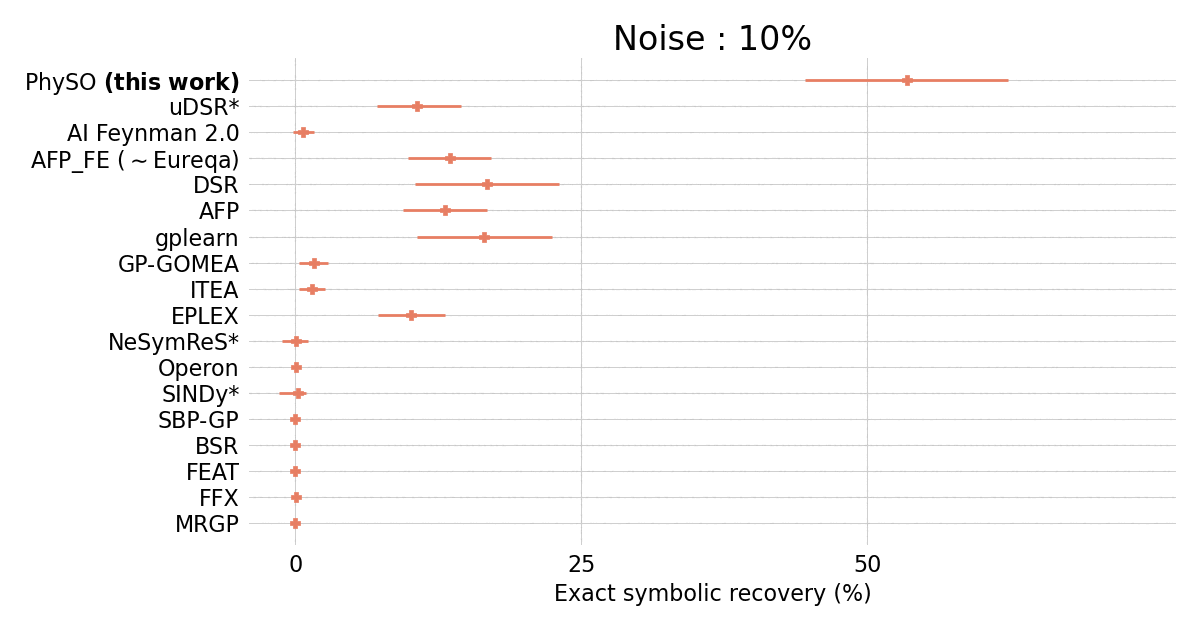
在从Feynman Lectures on Physics中包含120个表达式的标准费曼基准上，$\Phi$-SO相对于流行的SR包表现出色。

$\Phi$-SO在存在噪声（超过0.1%）的情况下取得了最先进的性能，即使在存在大量（10%）噪声的情况下也表现出稳健的性能：

安装

该包已在以下系统上进行了测试：

• Linux
• OSX（ARM & Intel）
• Windows

安装程序

虚拟环境

建议首先创建一个conda虚拟环境来安装该包：

conda create -n PhySO python=3.8

并激活它：

conda activate PhySO

下载

可以使用git下载physo：

git clone https://github.com/WassimTenachi/PhySO

或通过直接下载仓库的zip文件：这里

依赖项

从仓库根目录开始：

安装依赖项：

conda install --file requirements.txt

为了简化安装过程，自其第一个版本以来，physo已更新为仅具有最小的非常标准的依赖项。

---

注意：physo支持CUDA，但应注意，由于代码的瓶颈是自由常数优化，使用CUDA（即使在非常高端的GPU上）不会提高性能，甚至可能会降低性能。

---

安装PhySO

将physo安装到环境中（从仓库根目录）：

python -m pip install -e .

测试安装

导入测试：

python3
>>> import physo

这应该会导致physo成功导入。

单元测试：

运行所有单元测试（不包括并行模式的测试）（从仓库根目录）：

python -m unittest discover -p "*UnitTest.py"

这应该会导致所有测试成功通过。

运行所有单元测试（从仓库根目录）：

python -m unittest discover -p "*Test.py"

这应该会根据你的系统需要5-15分钟（如果你有很多CPU核心，效率曲线的制作会更长）。

卸载

卸载该包。

conda deactivate
conda env remove -n PhySO

入门（SR）

在本教程中，我们展示了如何使用physo进行符号回归（SR）。 本教程的参考笔记本可以在这里找到：sr_quick_start.ipynb。

设置

导入必要的库：

# 外部包
import numpy as np
import matplotlib.pyplot as plt
import torch

导入physo：

# 内部代码导入
import physo
import physo.learn.monitoring as monitoring

建议固定种子以实现可重复性：

# 种子
seed = 0
np.random.seed(seed)
torch.manual_seed(seed)

制作合成数据集

制作一个玩具合成数据集：

# 制作玩具合成数据
z = np.random.uniform(-10, 10, 50)
v = np.random.uniform(-10, 10, 50)
X = np.stack((z, v), axis=0)
y = 1.234*9.807*z + 1.234*v**2

应该注意到，自由常数搜索默认从1开始。因此，当使用默认超参数时，建议将数据归一化到1的数量级。

---

DA注释：
$\Phi$-SO可以利用DA（维度分析）使SR更高效。
可以考虑物理单位$X=(z,v)$，$z$是长度，维度$L^{1}, T^{0}, M^{0}$, $v$是速度，维度$L^{1}, T^{-1}, M^{0}$, $y=E$是能量，维度$L^{2}, T^{-2}, M^{1}$。 如果你不在处理物理问题，且所有变量/常数都是无量纲的，请不要指定任何xx_units参数（或为所有变量/常数指定[0,0]），physo将执行无量纲的符号回归任务。

---

数据集绘图：

n_dim = X.shape[0]
fig, ax = plt.subplots(n_dim, 1, figsize=(10,5))
for i in range (n_dim):
    curr_ax = ax if n_dim==1 else ax[i]
    curr_ax.plot(X[i], y, 'k.',)
    curr_ax.set_xlabel("X[%i]"%(i))
    curr_ax.set_ylabel("y")
plt.show()

SR配置

应该注意到，physo的SR能力高度依赖于超参数，因此建议根据你的具体问题调整超参数以进行科学研究。
目前可用的超参数预设配置的汇总：

配置	推荐用例	速度	效果	备注
config0	演示	★★★	★	轻便快捷的配置。
config1	SR与DA$^$；类SR与DA$^$	★	★★★	用于费曼基准和MW流基准的配置。
config2	SR；类SR	★★	★★	用于类基准的配置。

$^*$ DA = 维度分析

建议用户编辑配置文件（它们可以在：physo/config/ 中找到）。
默认情况下使用config0，但建议根据推荐进行科学研究。

---

DA注释：

1. 在最初的几十次迭代中，神经网络通常仍在学习维度分析规则，导致大多数候选者被丢弃且未被学习，从而有效地导致一个小得多的批量大小（通常小10倍），从而使评估过程的计算成本大大降低。因此，推荐使用更高的批量大小配置，以帮助提供足够的学习信息给神经网络。

---

日志和可视化设置：

save_path_training_curves = 'demo_curves.png'
save_path_log             = 'demo.log'

run_logger     = lambda : monitoring.RunLogger(save_path = save_path_log,
                                                do_save = True)

run_visualiser = lambda : monitoring.RunVisualiser (epoch_refresh_rate = 1,
                                           save_path = save_path_training_curves,
                                           do_show   = False,
                                           do_prints = True,
                                           do_save   = True, )

运行SR

给定变量数据$(x_0,..., x_n)$（这里是$(z, v)$），根变量$y$（这里是$E$）以及自由常数和固定常数，你可以通过以下命令运行SR任务以恢复$f$。

---

DA注释：
这里我们允许使用一个固定常数1，维度$L^{0}, T^{0}, M^{0}$（即无量纲）和自由常数$m$的维度$L^{0}, T^{0}, M^{1}$和$g$的维度$L^{1}, T^{-2}, M^{0}$。
应该注意到，这里的单位向量大小为3（例如：[1, 0, 0]），因为在这个例子中，变量的单位仅依赖于长度、时间和质量。 然而，单位向量的大小可以$\leq 7$只要在X、y和常数之间是一致的，允许用户表示任何单位（依赖于长度、时间、质量、温度、电流、光量或物质量）。 此外，无论单位的顺序如何，维度分析都可以进行，只要在X、y和常数之间保持一致使用任何顺序（[长度、质量、时间]或[质量、时间、长度]等）。

# 运行SR任务
expression, logs = physo.SR(X, y,
                            # 给出变量的名称（用于显示）
                            X_names = [ "z"       , "v"        ],
                            # 关联的物理单位（如果不相关，忽略或传递零）
                            X_units = [ [1, 0, 0] , [1, -1, 0] ],
                            # 给出根变量的名称（用于显示）
                            y_name  = "E",
                            y_units = [2, -2, 1],
                            # 固定常数
                            fixed_consts       = [ 1.      ],
                            fixed_consts_units = [ [0,0,0] ],
                            # 自由常数名称（用于显示）
                            free_consts_names = [ "m"       , "g"        ],
                            free_consts_units = [ [0, 0, 1] , [1, -2, 0] ],
                            # 可用于构造f的符号操作
                            op_names = ["mul", "add", "sub", "div", "inv", "n2", "sqrt", "neg", "exp", "log", "sin", "cos"],
                            get_run_logger     = run_logger,
                            get_run_visualiser = run_visualiser,
                            # 运行配置
                            run_config = physo.config.config0.config0,
                            # 并行模式（仅在从Python脚本运行时可用，不能在笔记本中使用）
                            parallel_mode = False,
                            # 迭代次数
                            epochs = 20
)

### 检查发现的最佳表达式

__获取最佳表达式:__

找到的最佳表达式（在准确性上）返回在`expression`变量中：

best_expr = expression print(best_expr.get_infix_pretty())

                 2           

-g⋅m⋅z + -v⋅v⋅sin (1.0)⋅1.0⋅m

它也可以稍后从日志文件中加载：

import physo from physo.benchmark.utils import symbolic_utils as su import sympy

加载帕累托前沿表达式

pareto_expressions = physo.read_pareto_pkl("demo_curves_pareto.pkl")

最准确的表达式是帕累托前沿的最后一个：

best_expr = pareto_expressions[-1] print(best_expr.get_infix_pretty())

__显示:__

该表达式可以转换为...
一个Sympy表达式：

best_expr.get_infix_sympy()

-gmz - vvsin(1.0)**21.0m

一个Sympy表达式（带有评估的自由常数值）：

best_expr.get_infix_sympy(evaluate_consts=True)[0]

1.74275713004454v**2sin(1.0)**2 + 12.1018380702846*z

一个Latex字符串:

best_expr.get_infix_latex()

'\frac{m \left(- 1000000000000000 g z - 708073418273571 v^{2}\right)}{1000000000000000}'

一个Latex字符串（带有评估的自由常数值）：

sympy.latex(best_expr.get_infix_sympy(evaluate_consts=True))

'\mathtt{\text{[1.74275713004454v**2sin(1.0)**2 + 12.1018380702846*z]}}'

__获取自由常数值:__

best_expr.free_consts

FreeConstantsTable -> 类常数 (['g' 'm']) : (1, 2) -> 特殊常数 ([]) : (1, 0, 1)

best_expr.free_consts.class_values

tensor([[ 6.9441, -1.7428]], dtype=torch.float64)

### 检查精确的符号恢复

转换为Sympy

best_expr = best_expr.get_infix_sympy(evaluate_consts=True)

best_expr = best_expr[0]

打印简化的最佳表达式和四舍五入的常数

print("best_expr : ", su.clean_sympy_expr(best_expr, round_decimal = 4))

目标表达式是：

target_expr = sympy.parse_expr("1.2349.807z + 1.234*v**2") print("target_expr : ", su.clean_sympy_expr(target_expr, round_decimal = 4))

检查等效性

print("\nChecking equivalence:") is_equivalent, log = su.compare_expression( trial_expr = best_expr, target_expr = target_expr, handle_trigo = True, prevent_zero_frac = True, prevent_inf_equivalence = True, verbose = True, ) print("Is equivalent:", is_equivalent)

best_expr : 1.234v**2 + 12.1018z target_expr : 1.234v**2 + 12.1018z

检查等效性:
  -> 评估1.234*v**2 + 12.101838*z（目标）是否等效于1.74275713004454*v**2*sin(1.0)**2 + 12.1018380702846*z（试验）
   -> 简化的表达式 : 1.23*v**2 + 12.1*z
   -> 符号误差        : 0
   -> 符号比例     : 1
   -> 三角函数符号误差        : 0
   -> 三角函数符号比例     : 1
   -> 等效 : True
Is equivalent: True

# 文档

更多文档请见 [physo.readthedocs.io](https://physo.readthedocs.io/en/latest/)。

__符号回归__ 快速入门指南: [这里](https://physo.readthedocs.io/en/latest/r_sr.html#getting-started-sr)  

__类符号回归__ 快速入门指南: [这里](https://physo.readthedocs.io/en/latest/r_class_sr.html#getting-started-class-sr)  

# 引用此研究
 
符号回归与强化学习和量纲分析结合

@ARTICLE{PhySO_RL_DA, author = {{Tenachi}, Wassim and {Ibata}, Rodrigo and {Diakogiannis}, Foivos I.}, title = "{Deep Symbolic Regression for Physics Guided by Units Constraints: Toward the Automated Discovery of Physical Laws}", journal = {ApJ}, year = 2023, month = dec, volume = {959}, number = {2}, eid = {99}, pages = {99}, doi = {10.3847/1538-4357/ad014c}, archivePrefix = {arXiv}, eprint = {2303.03192}, primaryClass = {astro-ph.IM}, adsurl = {https://ui.adsabs.harvard.edu/abs/2023ApJ...959...99T}, adsnote = {Provided by the SAO/NASA Astrophysics Data System} }

类符号回归

@ARTICLE{PhySO_ClassSR, author = {{Tenachi}, Wassim and {Ibata}, Rodrigo and {Fran{\c{c}}ois}, Thibaut L. and {Diakogiannis}, Foivos I.}, title = "{Class Symbolic Regression: Gotta Fit 'Em All}", journal = {arXiv e-prints}, keywords = {Computer Science - Machine Learning, Astrophysics - Astrophysics of Galaxies, Astrophysics - Instrumentation and Methods for Astrophysics, Physics - Computational Physics}, year = 2023, month = dec, eid = {arXiv:2312.01816}, pages = {arXiv:2312.01816}, doi = {10.48550/arXiv.2312.01816}, archivePrefix = {arXiv}, eprint = {2312.01816}, primaryClass = {cs.LG}, adsurl = {https://ui.adsabs.harvard.edu/abs/2023arXiv231201816T}, adsnote = {Provided by the SAO/NASA Astrophysics Data System} }