grokfast

<div align="center"> <h1>Grokfast: 通过放大缓慢梯度</br>加速Grokking过程</h1>

Jaerin Lee* · Bong Gyun Kang* · Kihoon Kim · Kyoung Mu Lee

<h5 align="center">首尔国立大学</h5> <p align="left"> *表示贡献相同。 </p>

</div>

简述: 我们通过使用增强优化器放大参数梯度的低频分量来加速grokking现象。

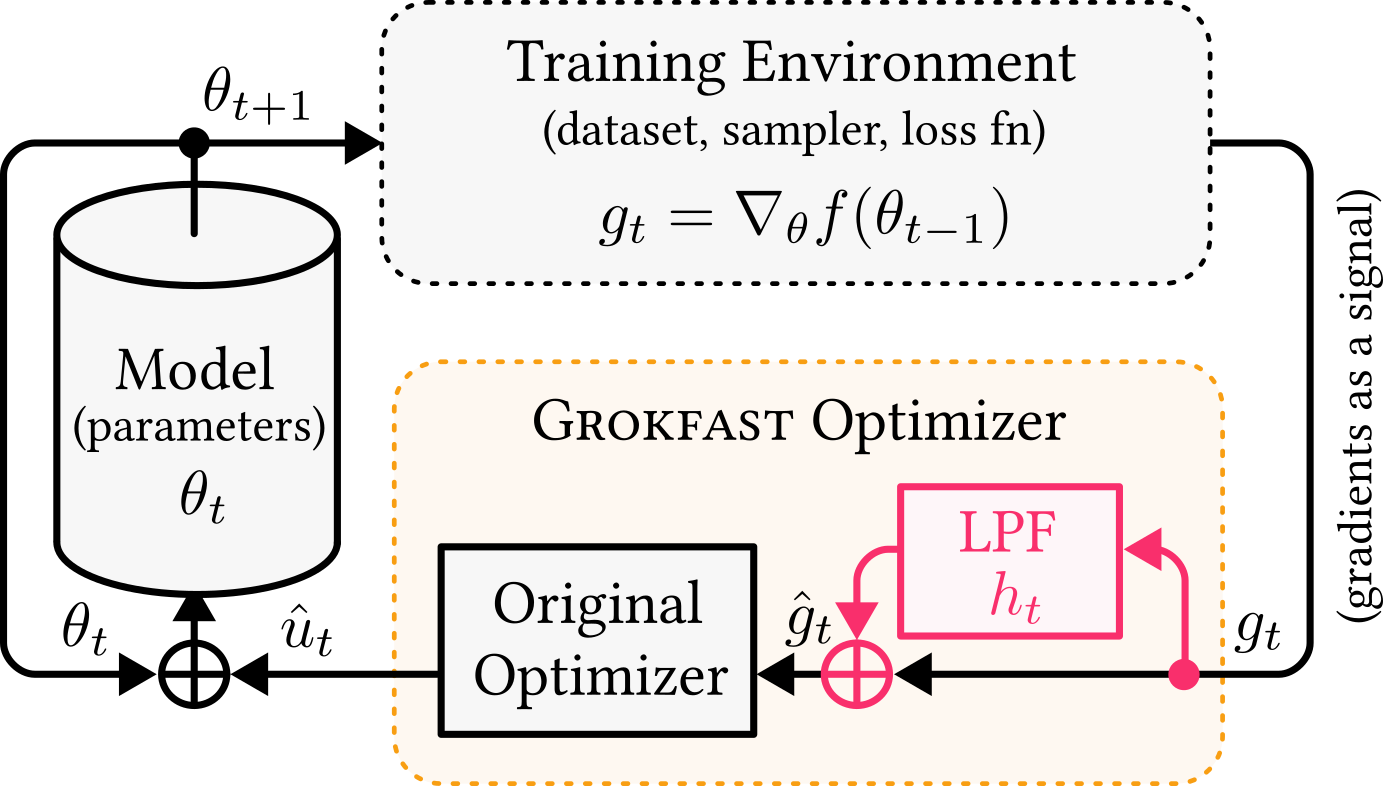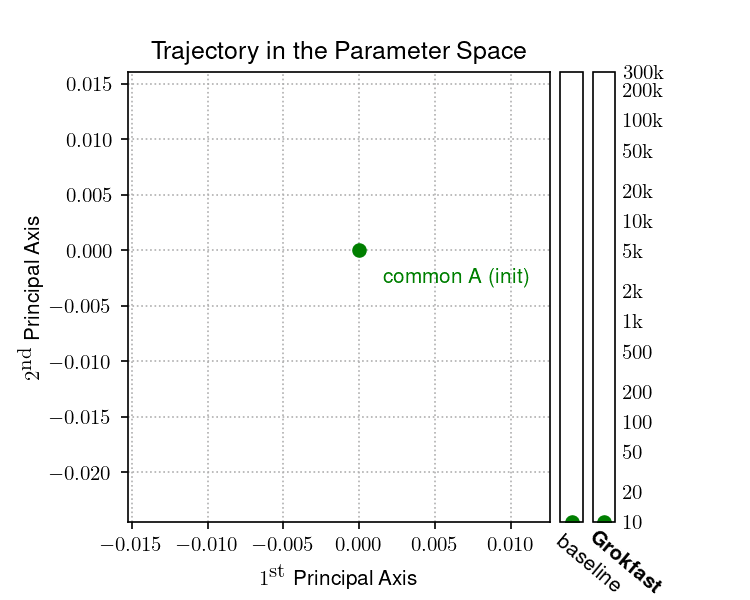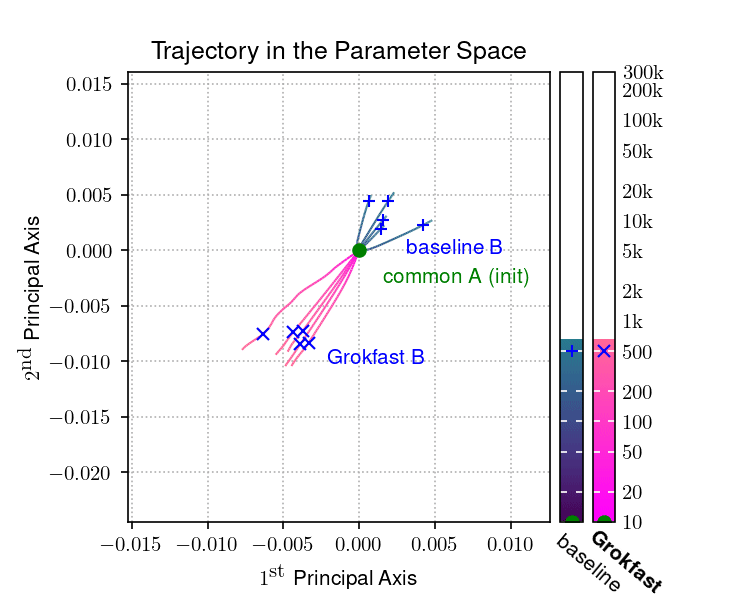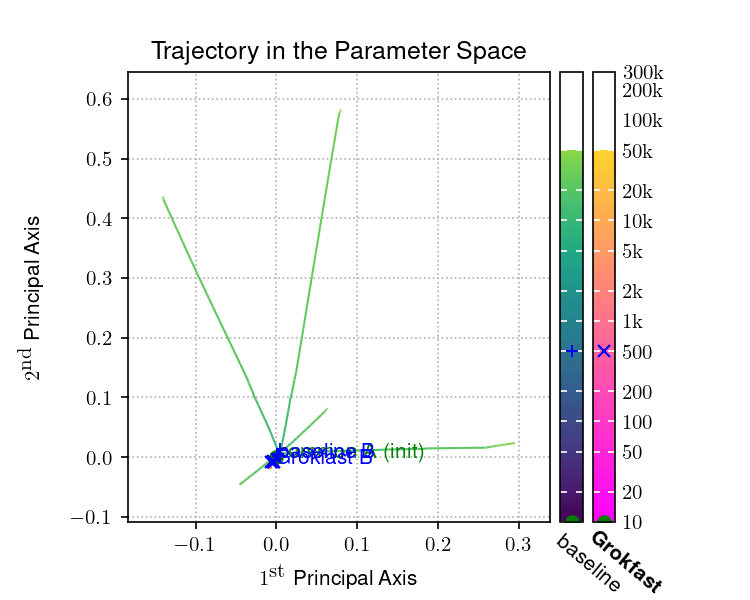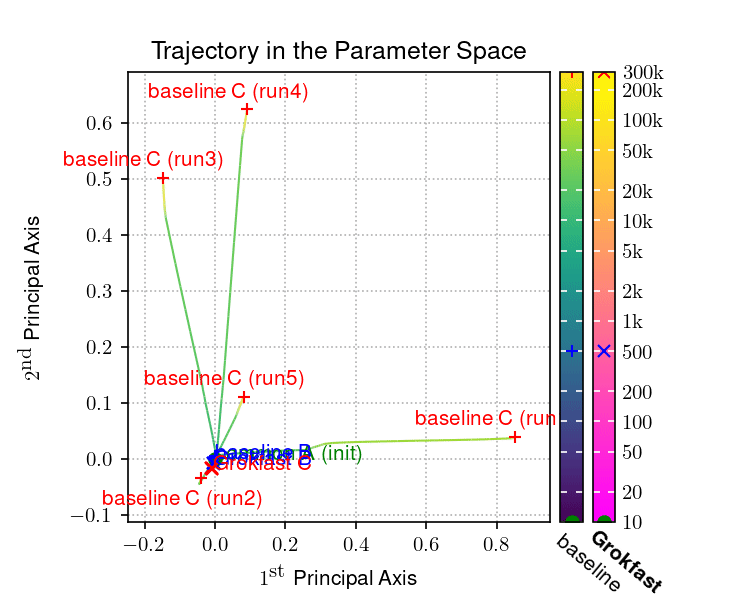摘要: 机器学习中一个令人困惑的现象被称为grokking，即在几乎完美地过拟合训练数据后，模型在数十倍的迭代次数后才实现延迟泛化。从机器学习实践者的角度出发，我们的目标是加速grokking现象下模型的泛化过程。通过将参数在训练迭代过程中的一系列梯度视为时间上的随机信号，我们可以将梯度下降下的参数轨迹在频谱上分解为两个部分：快速变化的、导致过拟合的部分和缓慢变化的、引导泛化的部分。这种分析使我们能够通过仅仅几行代码来放大梯度的缓慢变化部分，从而将grokking现象加速50倍以上。实验表明，我们的算法适用于涉及图像、语言和图形的各种任务，使这种突然泛化的特殊现象在实践中变得可用。

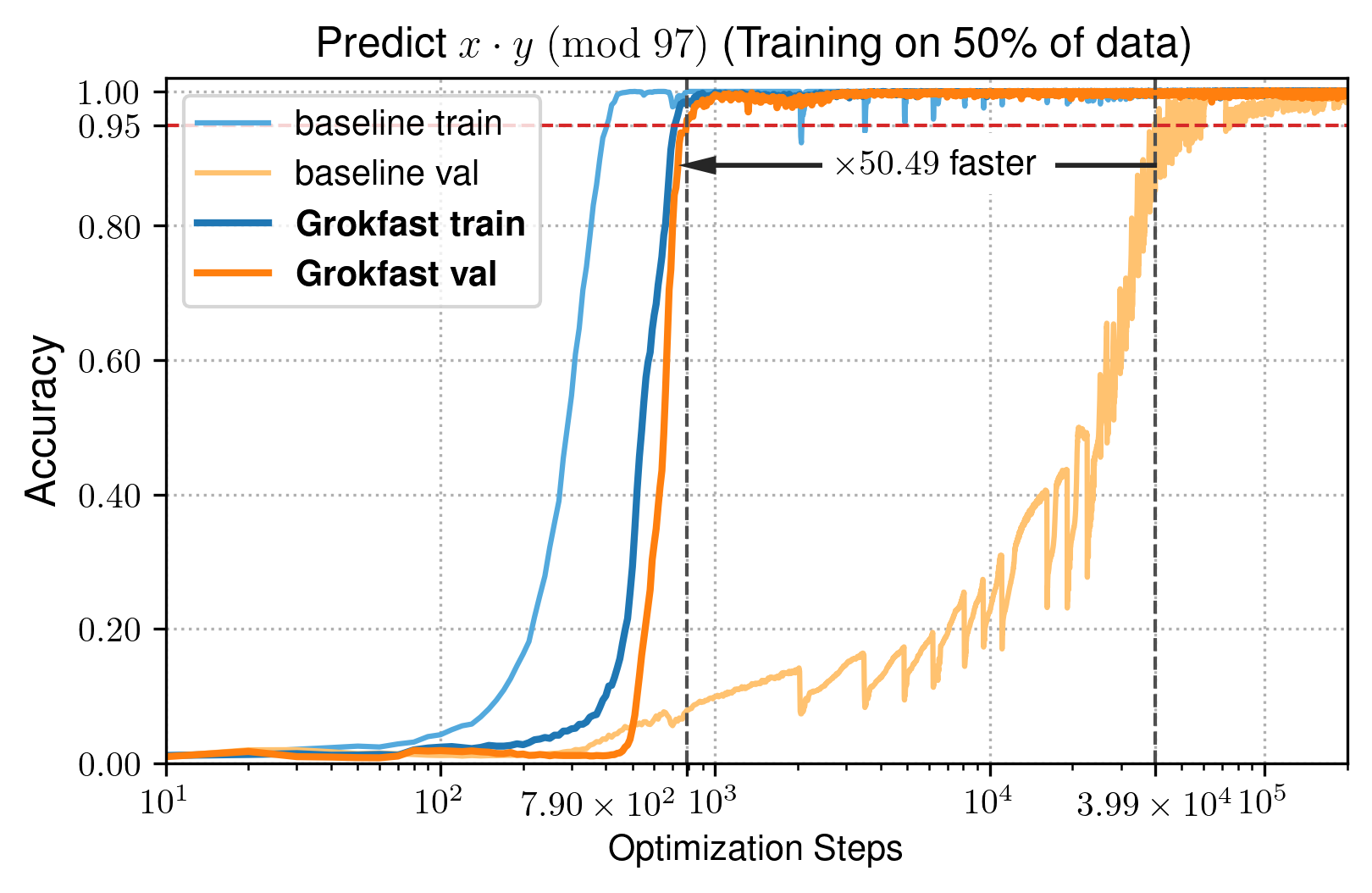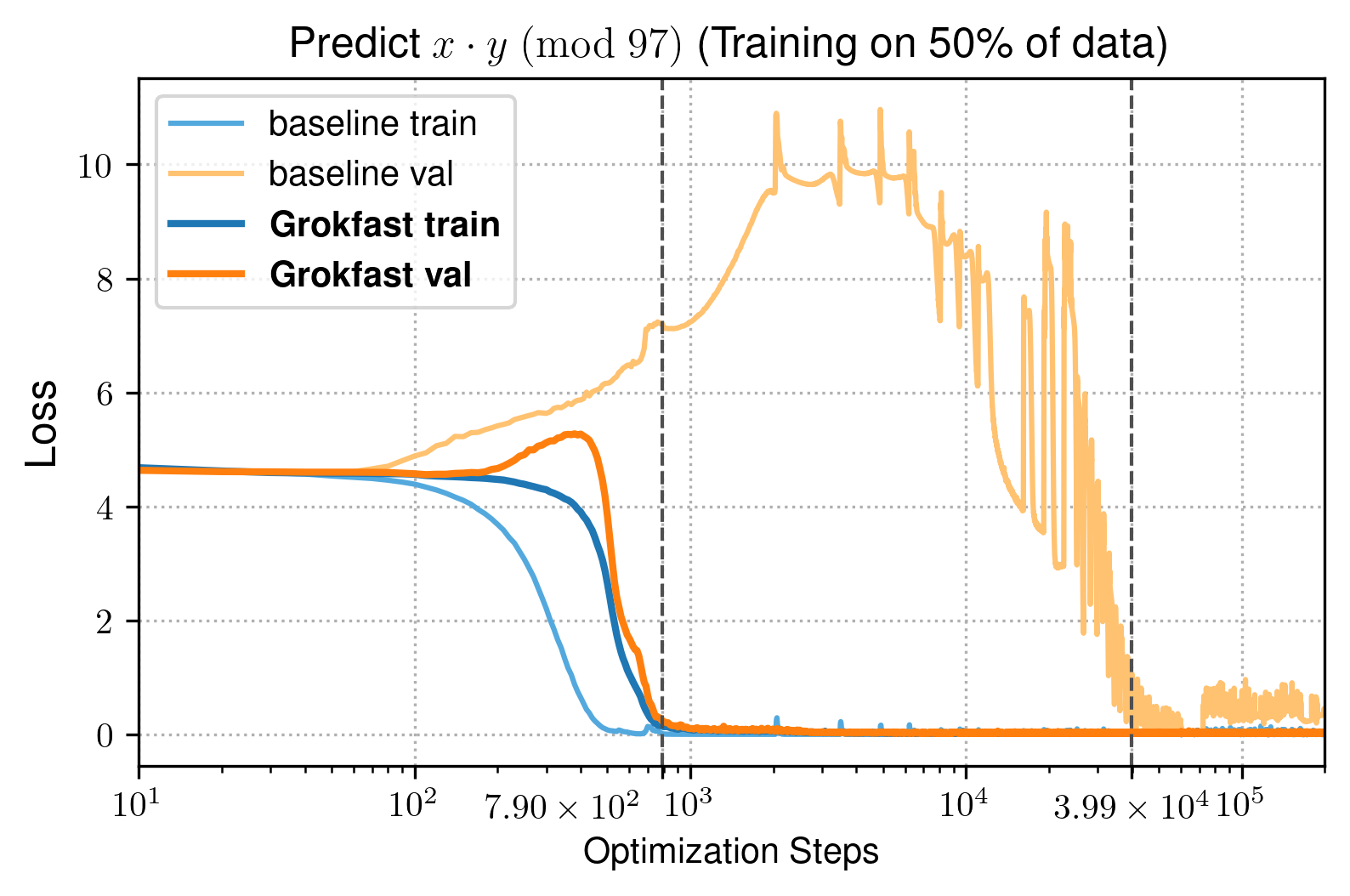使用方法

安装

Grokfast除了PyTorch外不需要额外的包。文件requirements.txt仅用于复现文章中的实验，如下面的复现部分所述。

说明

Grokfast可以通过在优化器调用前插入一行代码来应用。

从我们的仓库下载单个文件grokfast.py。

wget https://raw.githubusercontent.com/ironjr/grokfast/main/grokfast.py

导入辅助函数。

from grokfast import gradfilter_ma, gradfilter_ema

在训练循环之前插入以下行。

grads = None

在loss.backward()和optimizer.step()之间插入以下行之一。确保model的类型为nn.Module，并且grads在训练循环前正确初始化：

# ... 在优化循环中。
loss.backwards() # 计算梯度。

### 选项1：Grokfast（有参数alpha、lamb）
grads = gradfilter_ema(model, grads=grads, alpha=alpha, lamb=lamb)
### 选项2：Grokfast-MA（有参数window_size、lamb）
# grads = gradfilter_ma(model, grads=grads, window_size=window_size, lamb=lamb)

optimizer.step() # 调用优化器。
# ... 日志记录和其他代码。

完成！

<details> <summary>(2-1) ...或者，直接将方法复制粘贴到你的代码中！</summary>

### 导入
from collections import deque
from typing import Dict, Optional, Literal
import torch
import torch.nn as nn


### Grokfast
def gradfilter_ema(
    m: nn.Module,
    grads: Optional[Dict[str, torch.Tensor]] = None,
    alpha: float = 0.99,
    lamb: float = 5.0,
) -> Dict[str, torch.Tensor]:
    if grads is None:
        grads = {n: p.grad.data.detach() for n, p in m.named_parameters() if p.requires_grad}

    for n, p in m.named_parameters():
        if p.requires_grad:
            grads[n] = grads[n] * alpha + p.grad.data.detach() * (1 - alpha)
            p.grad.data = p.grad.data + grads[n] * lamb

    return grads


### Grokfast-MA
def gradfilter_ma(
    m: nn.Module,
    grads: Optional[Dict[str, deque]] = None,
    window_size: int = 128,
    lamb: float = 5.0,
    filter_type: Literal['mean', 'sum'] = 'mean',
    warmup: bool = True,
    trigger: bool = False,
) -> Dict[str, deque]:
    if grads is None:
        grads = {n: deque(maxlen=window_size) for n, p in m.named_parameters() if p.requires_grad}

    for n, p in m.named_parameters():
        if p.requires_grad:
            grads[n].append(p.grad.data.detach())

            if not warmup or len(grads[n]) == window_size and not trigger:
                if filter_type == "mean":
                    avg = sum(grads[n]) / len(grads[n])
                elif filter_type == "sum":
                    avg = sum(grads[n])
                else:
                    raise ValueError(f"无法识别的filter_type {filter_type}")
                p.grad.data = p.grad.data + avg * lamb

    return grads

</details>

参数

Grokfast (gradfilter_ema)
- m: nn.Module: 包含所有可训练参数的模型。
- grads: Optional[Dict[str, torch.Tensor]] = None: 运行中的内存（EMA）。通过设置为None进行初始化。之后递归地输入该方法的输出。
- alpha: float = 0.98: EMA的动量超参数。
- lamb: float = 2.0: 滤波器的放大因子超参数。
Grokfast-MA (gradfilter_ma)
- m: nn.Module: 包含所有可训练参数的模型。
- grads: Optional[Dict[str, deque]] = None: 运行中的内存（用于窗口移动平均的队列）。通过设置为None进行初始化。之后递归地输入该方法的输出。
- window_size: int = 100: 滤波器窗口的宽度。额外的内存需求随窗口大小线性增加。
- lamb: float = 5.0: 滤波器的放大因子超参数。
- filter_type: Literal['mean', 'sum'] = 'mean': 运行队列的聚合方法。
- warmup: bool = True: 如果为真，则在队列填满之前不应用滤波器。
- trigger: bool = False: 仅用于消融研究。如果为真，则不应用滤波器。

复现

我们还注意到每次运行所需的额外计算资源。时间和内存成本是在单个GTX 1080 Ti GPU上测量的。

安装

这将安装额外的包来预处理每个数据并总结结果。

conda create -n grok python=3.10 && conda activate grok
git clone https://github.com/ironjr/grokfast
pip install -r requirements.txt

算法数据（Transformer解码器，Grokfast-MA）

运行	达到95%验证准确率的迭代次数	达到95%验证准确率的壁钟时间（秒）	VRAM需求（MB）	每次迭代的延迟（秒）
基线	39890	5984	290	0.15
Grokfast-MA	790（$\times$ 50.49 $\downarrow$）	292（$\times$ 20.49 $\downarrow$）	458	0.37

# python main.py --label test # 基线。
python main.py --label test --filter ma --window_size 100 --lamb 5.0 --weight_decay 0.01

算法数据（Transformer解码器，Grokfast）

运行	达到95%验证准确率的迭代次数	达到95%验证准确率的壁钟时间（秒）	VRAM需求（MB）	每次迭代的延迟（秒）
基线	39890	5984	$290	0.15
Grokfast	910（$\times$ 43.84 $\downarrow$）	137（$\times$ 43.79 $\downarrow$）	294	0.15

# python main.py --label test # 基线。
python main.py --label test --filter ema --alpha 0.98 --lamb 2.0 --weight_decay 0.005

MNIST（MLP）

运行	达到95%验证准确率的迭代次数	达到95%验证准确率的壁钟时间（秒）	VRAM需求（MB）	每次迭代的延迟（毫秒）
基线	44022	1928	196	43.8
Grokfast	2001（$\times$ 22.00 $\downarrow$）	87.8（$\times$ 21.96 $\downarrow$）	198	43.9

# python main_mnist.py --label test # 基线。
python main_mnist.py --label test --alpha 0.8 --lamb 0.1 --weight_decay 2.0

IMDb（LSTM）

运行	最佳验证准确率	最小验证损失	显存需求 (MB)	每次迭代延迟 (ms)
基准线	0.84	0.517	754	20.4
Grokfast	0.90	0.412	762	21.2

训练前，从谷歌云盘或百度网盘（密码：vdp7）下载IMDb数据集。

# python main_imdb.py --label test # 基准线
python main_imdb.py --label test --alpha 0.98 --lamb 2.0 --weight_decay 10.0

QM9 (G-CNN)

运行	最小验证损失	显存需求 (MB)	每次迭代延迟 (ms)
基准线	0.00659	216	40.2
Grokfast	0.00348	216	41.4

# python main_qm9.py --label test # 基准线
python main_qm9.py --label test --alpha 0.9 --lamb 1.0 --weight_decay 0.01

常见问题

选择合适的超参数

这些建议基于我在主论文中展示的实验经验。这可能不适用于所有其他问题，也许更智能的技术能比这个程序做得更好。因此，请将这些作为设计自己过滤器的可能起点指南。

截止参数：本工作使用MA/EMA过滤器来实现过滤技术。截止频率由MA过滤器的窗口大小和EMA过滤器的动量参数决定。
1. 大致确定你想要实现的加速程度。 例如，在主论文中，截止参数是基于原始grokking报告确定的，实验表明泛化发生的速度比过拟合慢100倍。因此，我们希望实现N=100倍的加速。
2. 设置截止参数搜索的关键值。 对于MA，我开始将窗口大小设为"w=N=100"；对于EMA，我从满足"alpha^{N} = alpha^{100} = 0.1"的动量参数alpha开始（大约是alpha ~ 0.98）。
3. 在关键值附近进行超参数搜索。 我在(1.b)中设置的值附近扫描超参数值。
权重衰减：权重衰减像往常一样在优化器构造函数中设置（例如，optimizer = optim.Adam(m.parameters(), weight_decay=wd)）。
1. 从该任务的默认权重衰减开始。 例如，该任务最广泛使用的Github仓库选择的值。
2. 先固定权重衰减，尝试找到Grokfast过滤器参数（动量、窗口大小和幅度）的最优设置。 虽然权重衰减确实会影响最优过滤器参数的值，但根据我的经验，其影响似乎并不显著。
3. 开始增加权重衰减值。 从X1开始，然后尝试（X2、X5、X10）。我无法通过将默认值增加到X100倍来获得更好的结果。

致谢

我们的代码主要基于以下项目：

Ziming Liu等，"Omnigrok: Grokking Beyond Algorithmic Data"，ICLR 2023。[arXiv] [代码]
Alethea Power等，"Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets"，arXiv预印本arXiv:2201.02177。[arXiv] [代码]
@danielmamay的Grokking重新实现。[代码]

感谢你们提供有用的参考！

引用

如果您觉得我们的项目有用，请引用我们！

@article{lee2024grokfast,
    title={{Grokfast}: Accelerated Grokking by Amplifying Slow Gradients},
    author={Lee, Jaerin and Kang, Bong Gyun and Kim, Kihoon and Lee, Kyoung Mu},
    journal={arXiv preprint arXiv:2405.20233},
    year={2024}
}