最大更新参数化 (μP) 和超参数传输 (μTransfer)

论文链接 | 博客链接 | YouTube 视频

在 Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer 一文中，我们展示了，当我们以最大更新参数化 (μP) 来参数化模型时，最佳超参数在神经网络规模上的稳定性。这可以用来调试极大的神经网络，比如我们工作的预训练大型转换模型。更普遍地说，μP 减少了从探索到扩展的脆弱性和不确定性，这些在深度学习文献中往往没有明确提及。

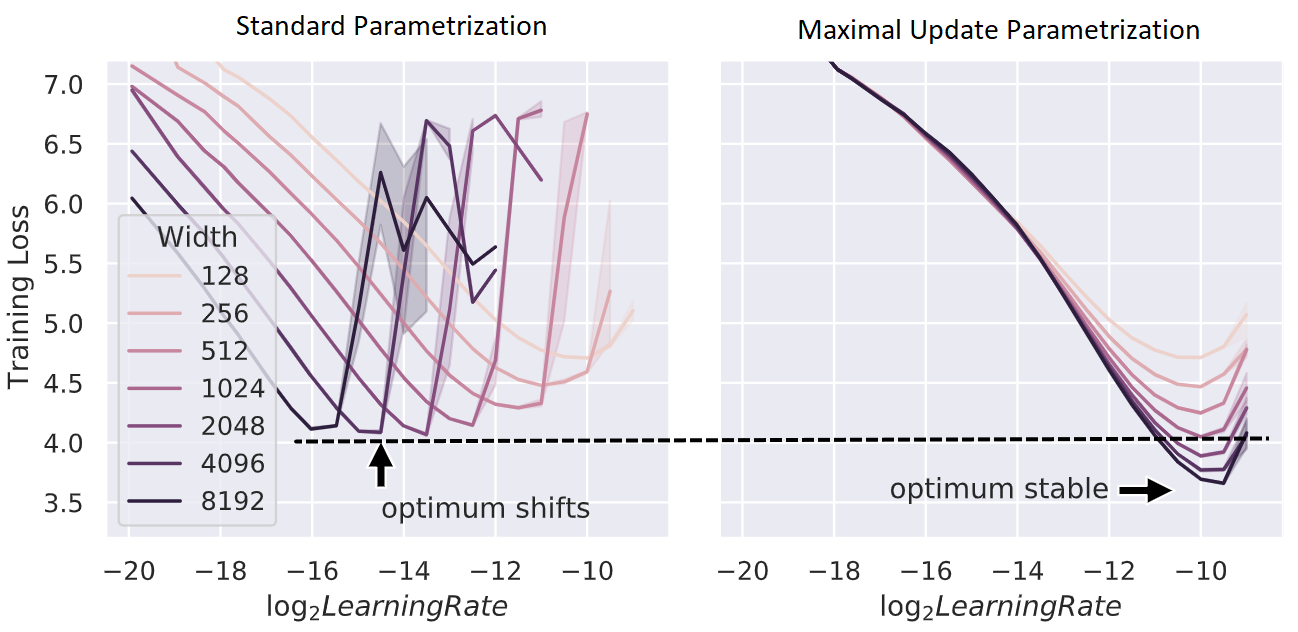上图：用 Adam 训练的不同 d_model 的变压器上的训练损失对学习率的变化情况。

μP 证明是唯一一种在宽度上具有这种超参数稳定性特性的“自然”参数化方法，在下面的 gif 中对用 SGD 训练的 MLP 进行了实证验证。这里，时间的推移，我们在 PyTorch 的默认学习率和 μP 的学习率和初始化缩放规则之间进行插值，并使用这种插值缩放规则将宽度为 256 的模型 (log2(width)=8) 缩放到宽度 2^13 = 8192（左图）。

这个仓库包含 mup 包的源代码，我们的工具使在 Pytorch 模型中实现 μP 变得轻松且错误率更低。

安装

pip install mup

源码安装

克隆该仓库，切换到其目录，并执行

pip install -r requirements.txt
pip install -e .

基本用法

from mup import MuReadout, make_base_shapes, set_base_shapes, MuSGD, MuAdam

class MyModel(nn.Module):
    def __init__(self, width, ...):
        ...
        ### 在模型定义中，将输出层替换为 MuReadout
        # readout = nn.Linear(width, d_out)
        readout = MuReadout(width, d_out)
        ### 如果与输入 nn.Embedding 层绑定权重，执行
        # readout = MuSharedReadout(input_layer.weight)
        ...
    def forward(self, ...):
        ...
        ### 如果使用 transformer，请确保使用
        ###   1/d 而不是 1/sqrt(d) 的注意力缩放
        # attention_scores = query @ key.T / d**0.5
        attention_scores = query @ key.T * 8 / d
        ### 我们在这里使用 8/d 以与 d=64 (常见的头维度) 的 1/d**0.5 兼容
        ...

### 实例化一个基础模型
base_model = MyModel(width=1)
### 可选择地，使用 `torchdistx.deferred_init.deferred_init` 来避免实例化参数
### 只需安装 `torchdistx` 并使用
# base_model = torchdistx.deferred_init.deferred_init(MyModel, width=1)
### 实例化一个“增量”模型，在所有希望扩展的维度（“宽度”）上与基础模型不同。
### 这里很简单，但在 transformer 中，例如，你可能希望同时扩展 nhead 和 dhead，所以增量模型应该在两者上都不同。
delta_model = MyModel(width=2) # 可选择地使用 `torchdistx` 来避免实例化

### 实例化目标模型（你实际想要训练的模型）。
### 这应该与基础模型相同，只是宽度可能不同。
### 特别是，base_model 和 model 应具有相同的深度。
model = MyModel(width=100)

### 设置基础形状
### 当 `model` 的参数形状与 `base_model` 相同时，
###   `model` 的行为与 `base_model` 完全相同
###   （这在 PyTorch 的默认参数化中）。
###   这在特定的模型大小下提供了向后兼容性。
###   否则，`model` 的初始化和 LR 将按 μP 规模化。
### 重要：应尽快调用它，
###   在重新初始化和优化器定义之前。
set_base_shapes(model, base_model, delta=delta_model)

### 或者，可以将基础模型形状保存到文件中
# make_base_shapes(base_model, delta_model, filename)
### 然后可以直接从文件名设置基础形状
# set_base_shapes(model, filename)
### 这在无法同时将 base_model 和 model 装入内存时很有用

### 替换你的自定义初始化（如果有）
for param in model.parameters():
    ### 如果用固定标准差或边界手动初始化，
    ### 则使用 mup.init 的相同函数替换
    # torch.nn.init.uniform_(param, -0.1, 0.1)
    mup.init.uniform_(param, -0.1, 0.1)
    ### 同样地，如果使用
    ###   `xavier_uniform_, xavier_normal_, kaiming_uniform_, kaiming_normal_`
    ### 来自 `torch.nn.init`，请用来自 `mup.init` 的相同函数替换

### 使用 `mup.optim` 中的优化器而不是 `torch.optim`
# optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
optimizer = MuSGD(model.parameters(), lr=0.1)

### 然后正常训练即可

请注意基础模型和增量模型不需要训练 —— 我们只是从中提取参数形状信息。因此，选择性地，我们可以使用 torchdistx 中的 deferred_init 函数来避免实例化这些潜在的大模型。在安装 torchdistx 后，使用 torchdistx.deferred_init.deferred_init(MyModel, **args) 代替 MyModel(**args)。有关更多详细信息，请参阅此页面。在我们提供的 MLP 和 Transformer 示例（不包括 mutransformers）中，可以通过传递 --deferred_init 来激活此功能。

`mup` 的内部工作原理

调用 set_base_shapes(model, ...) 时，model 的每个参数张量 p 都会获得一个 p.infshape 属性，该属性存储针对其每个维度的相应基础维度，以及该维度是否应被视为“无限” (即将被放大/缩小，例如 transformer 的 d_model) 或“有限”（即将固定，例如词汇表大小）。这些信息用于初始值设定项和优化器，以自动缩放参数或学习率以符合 μP。例如，隐藏权重 p 的 Adam 学习率计算为 globalLR / p.infshape.width_mult()，其中 p.infshape.width_mult() 基本上计算 fan_in / base_fan_in。

当前限制

set_base_shapes(model, ...) 假设 model 是以标准方式随机初始化的，并使用基础形状信息重新标定其参数以使模型处于 μP 中。
如果需要数据并行性，请使用 torch.nn.parallel.DistributedDataParallel 而不是 torch.nn.DataParallel。这是因为后者会删除 mup 包添加到模型每个参数张量的属性。此外，性能方面，pytorch 也推荐前者。
我们通过从传递给 mup 优化器的参数组中创建精细化的参数组，并通过操纵这些组中的 lr 属性来显式地根据 μP 缩放学习率。这与 PyTorch 的学习率调度器兼容。然而，如果你自己编写请确保调度器相对地设置学习率。下面是一个不该做的示例以及可以接受的替代方式：

optimizer = mup.MuAdam(model.parameters(), lr=1e-3)
for pg in optimizer.param_groups:
  # 不该做的：绝对地设置学习率
  # pg['lr'] = 1e-3 * 2
  # 可以接受的替代方式：相对地设置
  pg['lr'] *= 2

默认情况下，任何具有两个“无限”维度（即与基础维度不同的维度）的参数矩阵都被 mup 视为 (fan_out, fan_in) 形状，即在前向传递时，该矩阵右乘其输入。这与 pytorch 的所有 nn.Linear 权重的情况相同。如果你有一个自定义参数，例如 W，违反了此约定，你可以手动设置 W.infshape.main_idx = 0; W.infshape.main = W.infshape[0]，以让 mup 知道其形状对应于 (fan_in, fan_out)。如果你有一个参数张量，它有多个维度，但只有两个“无限”维度，其中第一个是 fan_in，第二个是 fan_out，则情况类似。
当前， torch.save 尚未存储附加到每个参数张量的 infshape 对象。在此问题修复之前，需在加载模型检查点后手动设置基础形状，如以下所示：

model = torch.load('my/model/path.pt')
# 重要：注意标志 `rescale_params=False`！
set_base_shapes(model, 'my/base/shape/path.bsh', rescale_params=False)

（set_base_shapes 默认重新标定 model 的参数，假设它是由 PyTorch 刚刚初始化的以符合 μP。rescale_params=False 标志关闭此行为。）

检查参数化的正确性

Coord 检查

就像梯度检查是一种简单的验证自动梯度实现正确性的方法，坐标检查 是一种简单的验证你是否正确实现了 μP 的方法：计算每个激活向量在训练前几步和不同宽度下的每个坐标的平均大小（我们在下面的 y 轴上用 l1 表示）。如果实现正确，那么我们会看到这个 l1 在很多宽度上保持稳定；否则，l1 会随着宽度增加而爆炸或缩小到 0。（我们本质上在检查下面描述的愿望 1。）（l1 计算 x.abs().mean() 对每个激活向量 x 的条目，而 l1 是“平均大小”的一种度量；可以类似地使用定义的 l2, l4 等，尽管它们可能随着随机种子的波动更大。）

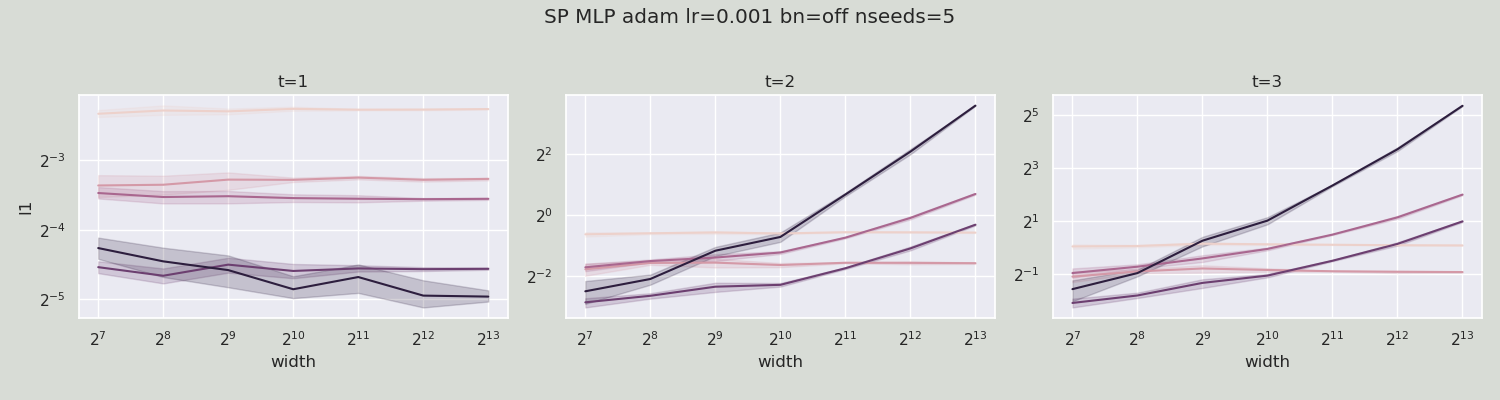
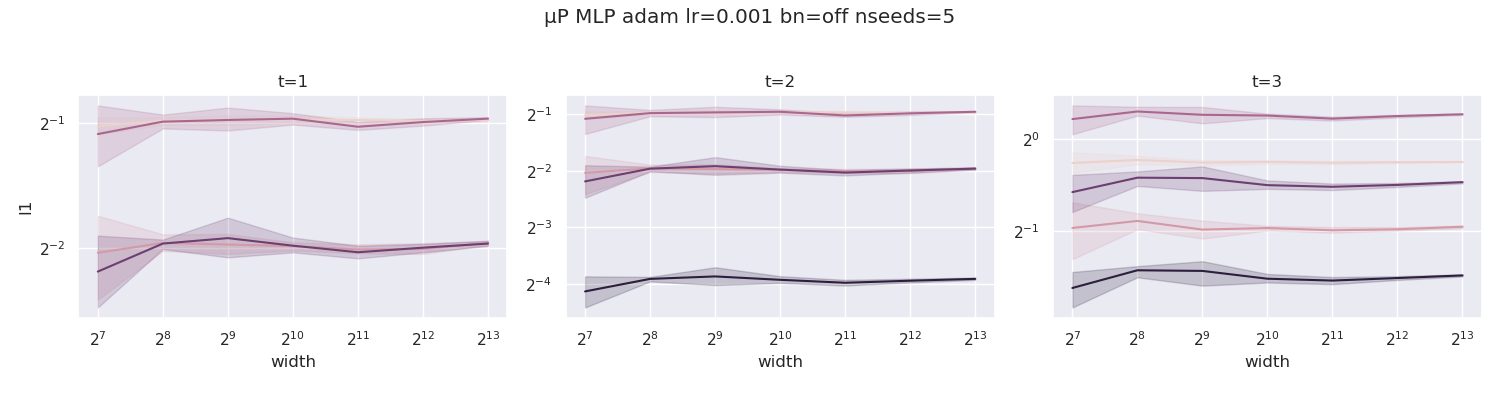
例如，在以下图中，我们绘制了 2 步训练的 width vs l1，其中 t=1 表示在初始化时，即在任何梯度更新之前。每条曲线对应于一层的（前）激活向量或网络的输出。第一组 3 个图显示了用 adam 训练的标准参数化 (SP) 的 MLP。我们看到在 1 步更新后，激活/输出 l1 随宽度爆炸。这意味着 SP 是“错误的”。我们现在对最大更新参数化 (μP) 的 MLP 做相同的处理（包括使用 mup.optim.MuAdam 而不是 torch.optim.Adam）。与上述情况相反，所有曲线保持水平，表明 μP 已正确实现。我们称这种检查实现正确性的方法为 coord 检查，即 “坐标检查”的简写。

制作自己的 Coord 检查图

我们提供了一种通过 mup.coord_check 模块中的函数实施此检查的方法。工作流程通常如下所示。

从mup.coord_check导入get_coord_data, plot_coord_data
# 构造一个包含不同宽度的lazy μP模型的字典
def lazy_model(width):
    # `set_base_shapes`返回模型
    return lambda: set_base_shapes(MyMuModel(width), 'my/base/shape/path.bsh')
    # 注意: 任何使用`mup.init`的自定义初始化也需要在lambda内部完成
models = {64: lazy_model(64), ..., 1024: lazy_model(1024)}
# 创建一个小批量/序列长度的数据加载器
#   仅用于测试
dataloader = ...
# 记录训练过程中模型激活的几步数据
# 返回一个pandas数据框
df = get_coord_data(models, dataloader)
# 保存坐标检查图到文件名。
plot_coord_data(df, save_to=filename)
# 如果你在jupyter笔记本中，你也可以执行`plt.show()`来显示图形

例如, `mup.coord_check.example_plot_coord_check`函数是这样为玩具MLP和CNN模型实现的。

如果你看到曲线在训练几步后随宽度膨胀或收缩到0，那么你的μP实现中存在bug（是否忘记在delta模型中变动了某个维度，如`d_ffn`）。
如果你看到曲线收敛到右边，那么你的实现很可能是正确的。
然而，有两个典型的例外：
在μP中，以下内容在初始化时会以1/sqrt(宽度)的速度收缩到0：
  - 网络输出
  - Transformer中的注意力logits

这些是暂时的，几步后它们的曲线应该大致平坦。
然而，为了在初始化时消除差异，我们建议：
   - 将输出层（应该是`MuReadout`实例）权重初始化为0，通过`readout_zero_init=True`选项
   - 将Transformer中的查询矩阵初始化为0（必须手动完成）。如果在初始化时需要打破注意力logits的对称性，请用非零方差初始化（相对）位置偏差。

#### 坐标检查提示

- 使用大的学习率（比你实际训练使用的学习率更大）。这将强调潜在的坐标爆炸问题，如果学习率太小，初始化可能会隐藏这些问题。
- 如果你在前向传递中多次重用一个模块，那么`mup.get_coord_data`将只记录最后一次使用的统计数据。在这种情况下，为了测试目的，可以用不同名称的`nn.Identity`模块包装不同的使用，以区分它们。

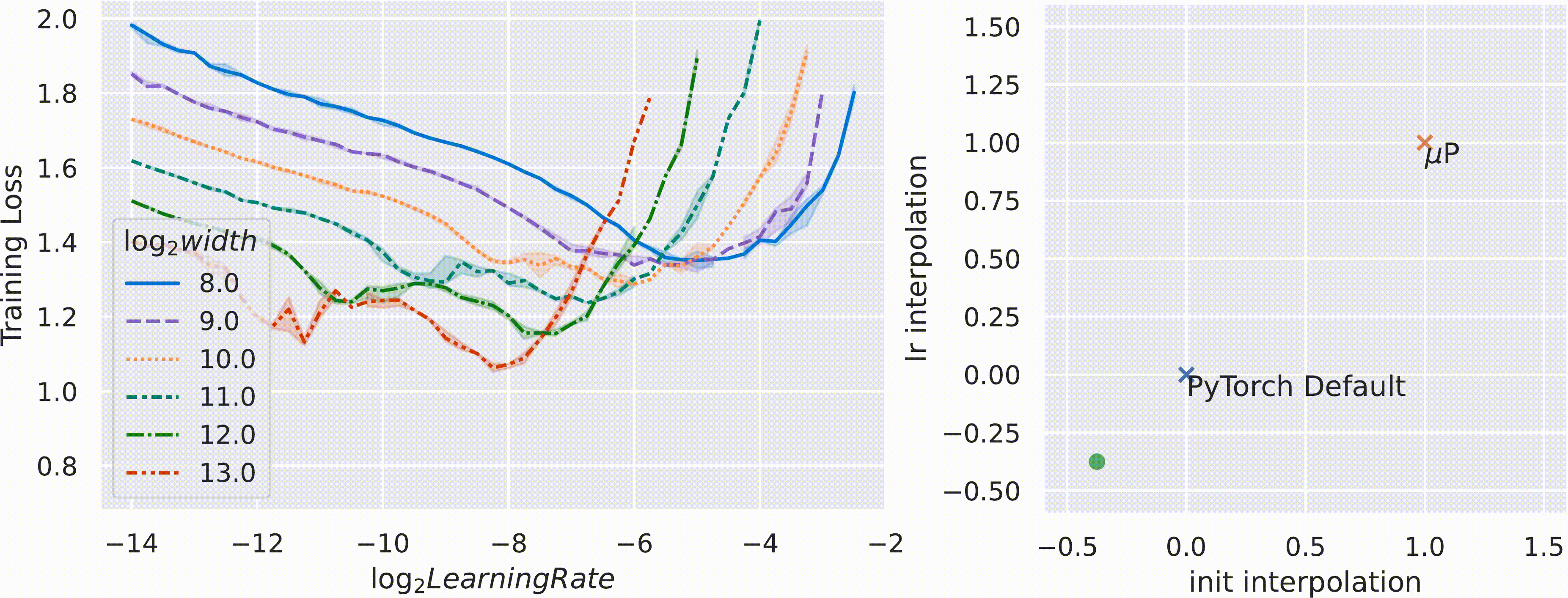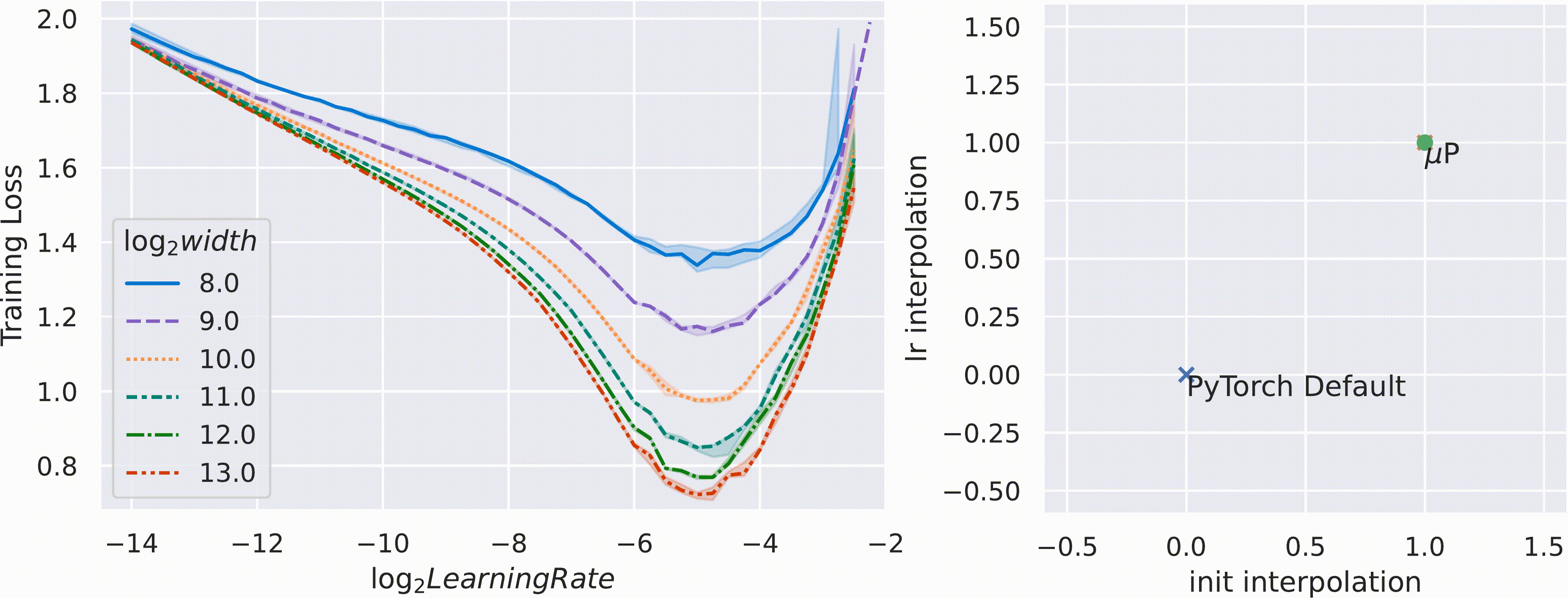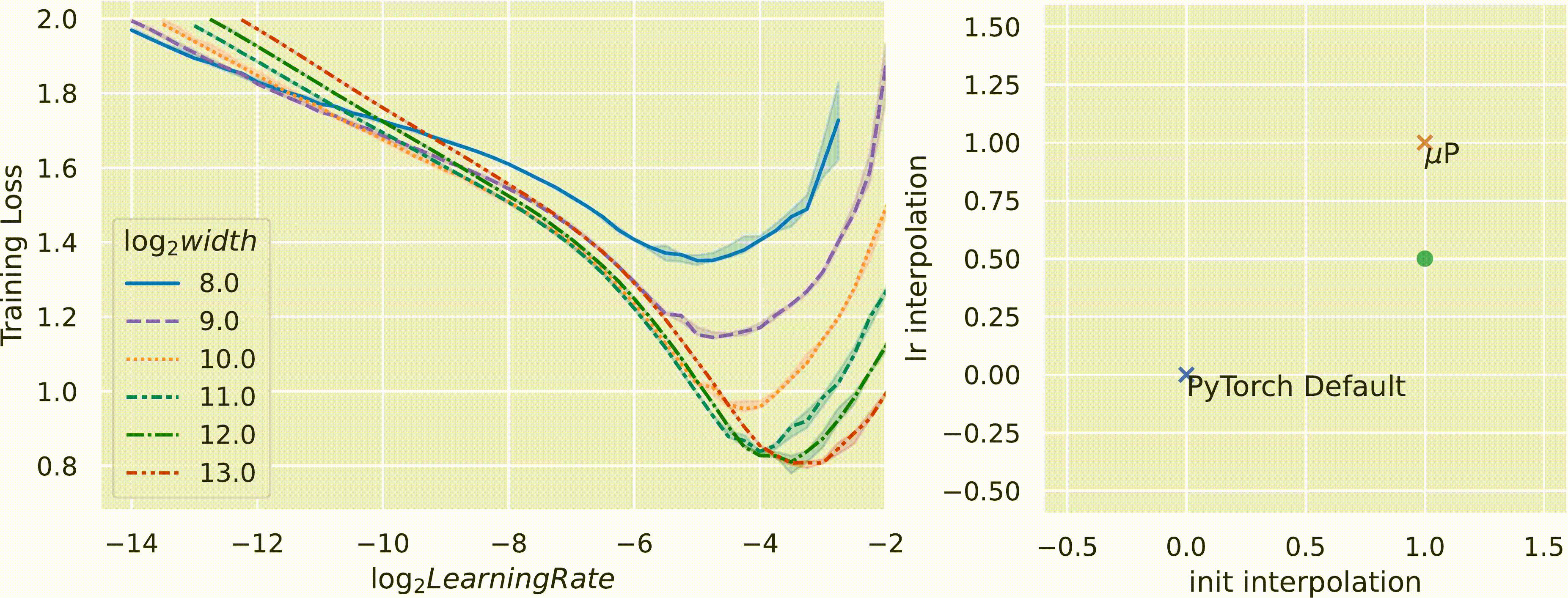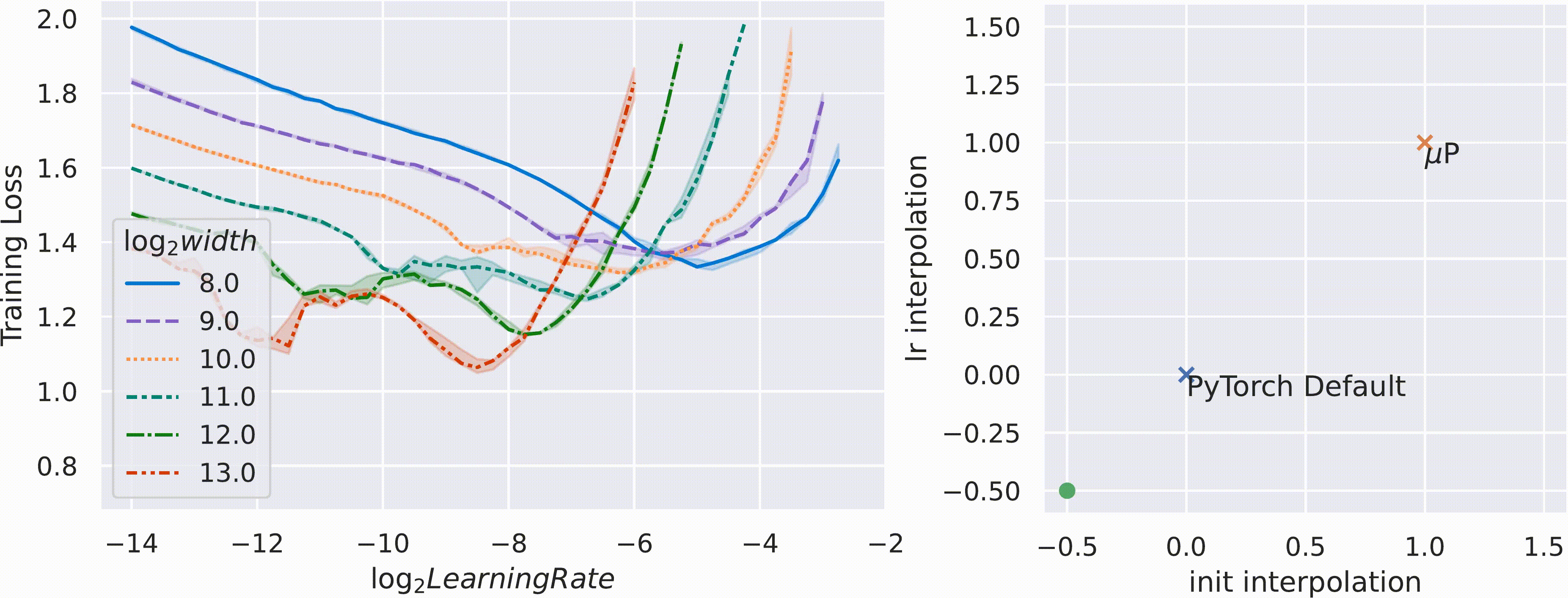
### 更宽总是更好

![](https://yellow-cdn.veclightyear.com/35dd4d3f/8ffef894-f713-4554-8b49-59e3fc3f08ca.png)

μP未正确实现的另一个迹象是，在某些训练宽度后，训练损失随扩宽变得更差。
上图展示了一组训练曲线：(左)正确实现应该始终看到性能随宽度在任何训练阶段都在提高；(中)如果你使用标准参数化（SP），有时你可能会看到性能随着宽度增加到某个点后突然变差；(右)或你可能会立即看到窄模型的性能变差。

## 示例
请参见`examples/`中的`MLP`、`Transformer`和`ResNet`文件夹，以及`mup/test`中的测试示例。
熟悉[Huggingface Transformers](https://github.com/huggingface/transformers)的人也可以找到`examples/mutransformers`子模块的示例说明（通过`git submodule update --init`获得），也可以单独在[https://github.com/microsoft/mutransformers](https://github.com/microsoft/mutransformers)上找到。

## 与Huggingface的原生集成

对你的[Huggingface Transformer](https://github.com/huggingface/transformers)在扩展时出现问题感到沮丧吗？
想在单个GPU上为大型多GPU [Huggingface Transformer](https://github.com/huggingface/transformers)调优超参数吗？
如果是这样，请为[这个github问题](https://github.com/huggingface/transformers/issues/16157)点赞！

## 运行测试
要运行测试，请执行
```bash
python -m mup.test

基本数学

μP旨在满足以下需求：

在训练期间的任何时候

网络中的每个（预）激活向量应具有Θ(1)大小的坐标

神经网络输出应为O(1)。

所有参数应尽可能多地更新（就宽度缩放而言），而不会导致发散

事实证明，这些需求唯一地确定了μP。要从这些需求中推导μP，需要仔细考虑向量Av的“坐标大小”，即方阵A乘向量v的结果，在A和v“相关”时如何依赖于它们的大小。这里可以将A视为权重，将v视为激活向量。这反过来又取决于A是哪种矩阵，v是哪种向量。在训练宽神经网络的背景下，实际上只需要考虑大致上具有独立同分布坐标的向量和两种矩阵：1）看起来像这些向量外积的矩阵，2）独立同分布的随机矩阵。类型1的矩阵涵盖诸如权重梯度的情况；类型2的矩阵涵盖诸如权重初始化的情况。

然后，如果A和v的条目大小都是Θ(1)并且它们在训练过程中相关，我们有以下表格。