captum

<hr/> <!--- 徽章：开始 --->

<!--- 徽章：结束 --->

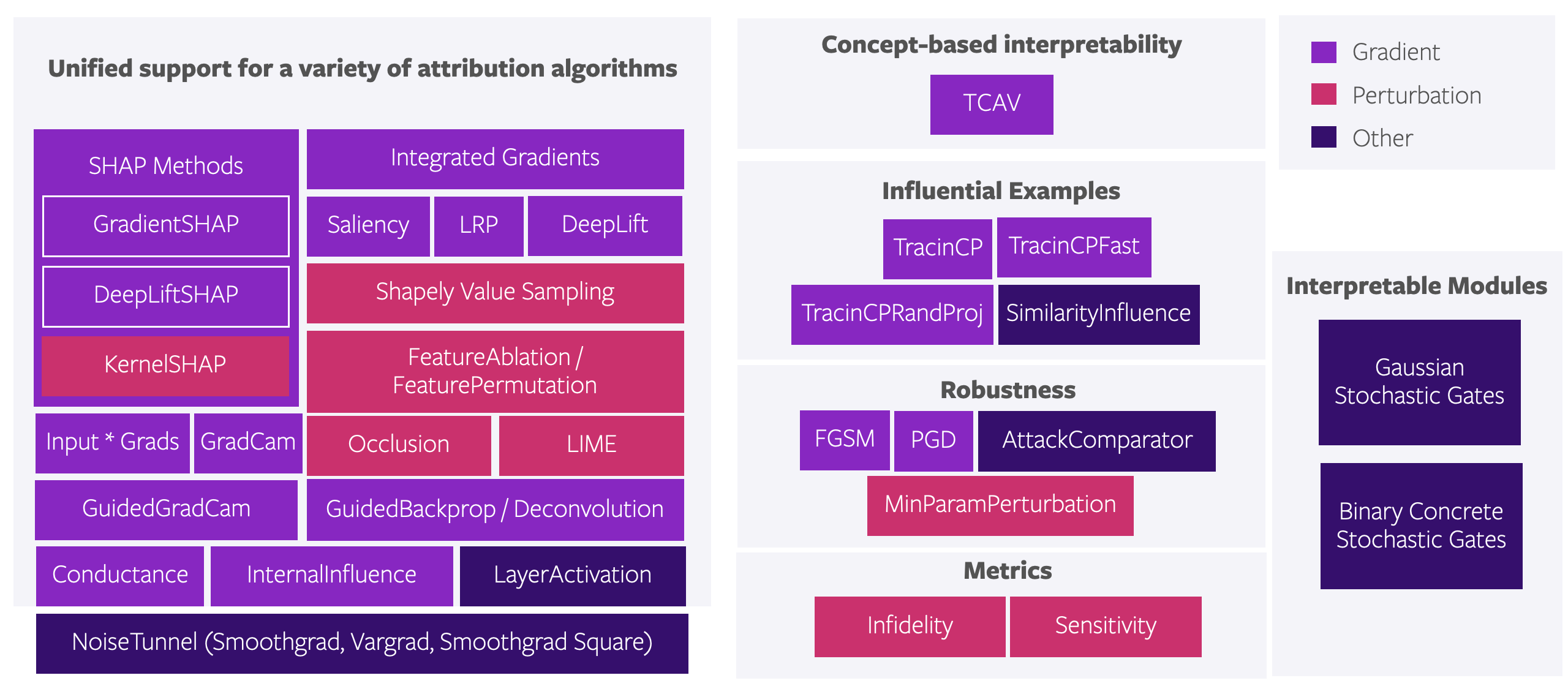
Captum是一个用于PyTorch的模型可解释性和理解库。Captum在拉丁语中意为理解，它包含了针对PyTorch模型的集成梯度、显著性图、平滑梯度、变分梯度等通用实现。它可以快速集成到使用特定领域库（如torchvision、torchtext等）构建的模型中。

Captum目前处于测试阶段，正在积极开发中！

关于Captum

随着模型复杂度的增加和由此导致的透明度缺失，模型可解释性方法变得越来越重要。模型理解既是一个活跃的研究领域，也是各行业使用机器学习的实际应用关注点。Captum提供了最先进的算法，如集成梯度、概念激活向量测试（TCAV）、TracIn影响函数等，为研究人员和开发人员提供了一种简单的方法来理解哪些特征、训练样本或概念对模型的预测有贡献，以及模型学习的内容和方式。此外，Captum还提供了对抗性攻击和最小输入扰动功能，可用于生成反事实解释和对抗性扰动。

Captum帮助机器学习研究人员更轻松地实现可以与PyTorch模型交互的可解释性算法。Captum还允许研究人员快速将他们的工作与库中现有的其他算法进行基准测试。

目标受众

Captum的主要受众是希望改进模型并了解哪些概念、特征或训练样本重要的模型开发人员，以及专注于识别能更好地解释多种模型类型的算法的可解释性研究人员。

Captum还可以被在生产中使用训练模型的应用工程师使用。Captum通过改进的模型可解释性提供了更简单的故障排除，并有潜力为最终用户提供更好的解释，说明为什么他们会看到特定内容，比如电影推荐。

安装

安装要求

• Python >= 3.8
• PyTorch >= 1.10

安装最新版本

Captum的最新版本可以通过Anaconda（推荐）或pip轻松安装。

使用conda

你可以从以下任何支持的conda渠道安装captum：

• 渠道：pytorch

  conda install captum -c pytorch

• 渠道：conda-forge

  conda install captum -c conda-forge

使用pip

pip install captum

手动/开发安装

如果你想尝试我们最新的功能（并且不介意偶尔遇到一些bug），你可以直接从GitHub安装最新的主分支。对于基本安装，运行：

git clone https://github.com/pytorch/captum.git
cd captum
pip install -e .

要自定义安装，你还可以运行以下变体：

• pip install -e .[insights]：同时安装运行Captum Insights所需的所有包。
• pip install -e .[dev]：同时安装开发所需的所有工具（测试、代码检查、文档构建；详见下方贡献）。
• pip install -e .[tutorials]：同时安装运行教程笔记本所需的所有包。

要从手动安装执行单元测试，运行：

# 运行单个单元测试
python -m unittest -v tests.attr.test_saliency
# 运行所有单元测试
pytest -ra

入门

Captum通过探索对模型预测有贡献的特征，帮助你解释和理解PyTorch模型的预测。 它还有助于理解哪些神经元和层对模型预测很重要。

让我们将其中一些算法应用于我们为演示目的创建的玩具模型。 为简单起见，我们将使用以下架构，但用户可以使用他们选择的任何PyTorch模型。

import numpy as np

import torch
import torch.nn as nn

from captum.attr import (
    GradientShap,
    DeepLift,
    DeepLiftShap,
    IntegratedGradients,
    LayerConductance,
    NeuronConductance,
    NoiseTunnel,
)

class ToyModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.lin1 = nn.Linear(3, 3)
        self.relu = nn.ReLU()
        self.lin2 = nn.Linear(3, 2)

        # 初始化权重和偏置
        self.lin1.weight = nn.Parameter(torch.arange(-4.0, 5.0).view(3, 3))
        self.lin1.bias = nn.Parameter(torch.zeros(1,3))
        self.lin2.weight = nn.Parameter(torch.arange(-3.0, 3.0).view(2, 3))
        self.lin2.bias = nn.Parameter(torch.ones(1,2))
def forward(self, input):
    return self.lin2(self.relu(self.lin1(input)))

让我们创建一个模型实例并将其设置为评估模式。

model = ToyModel()
model.eval()

接下来，我们需要定义简单的输入和基线张量。 基线属于输入空间，通常不携带预测信号。 零张量可以作为许多任务的基线。 一些可解释性算法，如IntegratedGradients、Deeplift和GradientShap，旨在将输入和基线之间的变化归因于神经网络输出的预测类别或值。

我们将在上述网络上应用模型可解释性算法，以了解个别神经元/层的重要性以及在最终预测中起重要作用的输入部分。

为了使计算具有确定性，让我们固定随机种子。

torch.manual_seed(123)
np.random.seed(123)

让我们定义我们的输入和基线张量。基线在一些可解释性算法中使用，如IntegratedGradients、DeepLift、GradientShap、NeuronConductance、LayerConductance、InternalInfluence和NeuronIntegratedGradients。

input = torch.rand(2, 3)
baseline = torch.zeros(2, 3)

接下来，我们将使用IntegratedGradients算法为每个输入特征分配归因分数，以针对第一个目标输出。

ig = IntegratedGradients(model)
attributions, delta = ig.attribute(input, baseline, target=0, return_convergence_delta=True)
print('IG Attributions:', attributions)
print('Convergence Delta:', delta)

输出：

IG Attributions: tensor([[-0.5922, -1.5497, -1.0067],
                         [ 0.0000, -0.2219, -5.1991]])
Convergence Delta: tensor([2.3842e-07, -4.7684e-07])

该算法为每个输入元素输出一个归因分数和一个收敛delta。收敛delta的绝对值越小，近似就越好。如果我们选择不返回delta，我们可以简单地不提供return_convergence_delta输入参数。返回的delta的绝对值可以被解释为每个输入样本的近似误差。它也可以作为给定输入和基线的积分近似准确度的代理。如果近似误差很大，我们可以通过将n_steps设置为更大的值来尝试更多的积分近似步骤。并非所有算法都返回近似误差。但那些返回的算法都是基于算法的完整性属性来计算的。

正的归因分数意味着该特定位置的输入对最终预测有正面贡献，负的则意味着相反。归因分数的大小表示贡献的强度。零归因分数意味着该特定特征没有贡献。

同样，我们可以将GradientShap、DeepLift和其他归因算法应用于模型。

GradientShap首先从基线分布中选择一个随机基线，然后对每个输入示例添加标准差为0.09的高斯噪声n_samples次。之后，它在每个示例-基线对之间选择一个随机点，并计算关于目标类（在本例中为target=0）的梯度。最终的归因是梯度 * (输入 - 基线)的平均值。

gs = GradientShap(model)

# 我们定义一个基线分布，并从该分布中抽取`n_samples`个样本，以估计所有基线的梯度期望
baseline_dist = torch.randn(10, 3) * 0.001
attributions, delta = gs.attribute(input, stdevs=0.09, n_samples=4, baselines=baseline_dist,
                                   target=0, return_convergence_delta=True)
print('GradientShap Attributions:', attributions)
print('Convergence Delta:', delta)

输出

GradientShap Attributions: tensor([[-0.1542, -1.6229, -1.5835],
                                   [-0.3916, -0.2836, -4.6851]])
Convergence Delta: tensor([ 0.0000, -0.0005, -0.0029, -0.0084, -0.0087, -0.0405,  0.0000, -0.0084])

Delta是为每个n_samples * input.shape[0]示例计算的。用户可以，例如，对它们取平均值：

deltas_per_example = torch.mean(delta.reshape(input.shape[0], -1), dim=1)

以获得每个示例的平均delta。

以下是如何在上述ToyModel上应用DeepLift和DeepLiftShap的示例。DeepLift的当前实现仅支持Rescale规则。有关替代实现的更多详细信息，请参阅DeepLift论文。

dl = DeepLift(model)
attributions, delta = dl.attribute(input, baseline, target=0, return_convergence_delta=True)
print('DeepLift Attributions:', attributions)
print('Convergence Delta:', delta)

输出

DeepLift Attributions: tensor([[-0.5922, -1.5497, -1.0067],
                               [ 0.0000, -0.2219, -5.1991])
Convergence Delta: tensor([0., 0.])

DeepLift为输入分配的归因分数与IntegratedGradients类似，但执行时间较短。关于DeepLift需要记住的另一个重要事项是，它目前不支持所有非线性激活类型。有关当前实现限制的更多详细信息，请参阅DeepLift论文。

与集成梯度类似，DeepLift为每个输入示例返回一个收敛delta分数。近似误差则是收敛delta的绝对值，可以作为算法近似准确度的代理。

现在让我们看看DeepLiftShap。与GradientShap类似，DeepLiftShap使用基线分布。在下面的示例中，我们使用与GradientShap相同的基线分布。

dl = DeepLiftShap(model)
attributions, delta = dl.attribute(input, baseline_dist, target=0, return_convergence_delta=True)
print('DeepLiftSHAP 归因:', attributions)
print('收敛误差:', delta)

输出

DeepLiftSHAP 归因: tensor([[-5.9169e-01, -1.5491e+00, -1.0076e+00],
                                   [-4.7101e-03, -2.2300e-01, -5.1926e+00]], grad_fn=<MeanBackward1>)
收敛误差: tensor([-4.6120e-03, -1.6267e-03, -5.1045e-04, -1.4184e-03, -6.8886e-03,
                           -2.2224e-02,  0.0000e+00, -2.8790e-02, -4.1285e-03, -2.7295e-02,
                           -3.2349e-03, -1.6265e-03, -4.7684e-07, -1.4191e-03, -6.8889e-03,
                           -2.2224e-02,  0.0000e+00, -2.4792e-02, -4.1289e-03, -2.7296e-02])

DeepLiftShap 使用 DeepLift 计算每个输入-基线对的归因分数，并对所有基线的每个输入取平均值。

它为每个输入示例-基线对计算增量，因此产生 input.shape[0] * baseline.shape[0] 个增量值。

与 GradientShap 类似，为了计算基于示例的增量，我们可以对每个示例取平均值：

deltas_per_example = torch.mean(delta.reshape(input.shape[0], -1), dim=1)

为了平滑并提高归因质量，我们可以通过 NoiseTunnel 运行 IntegratedGradients 和其他归因方法。 NoiseTunnel 允许我们使用 SmoothGrad、SmoothGrad_Sq 和 VarGrad 技术来平滑归因， 方法是聚合多个通过添加高斯噪声生成的噪声样本的归因。

以下是如何将 NoiseTunnel 与 IntegratedGradients 一起使用的示例。

ig = IntegratedGradients(model)
nt = NoiseTunnel(ig)
attributions, delta = nt.attribute(input, nt_type='smoothgrad', stdevs=0.02, nt_samples=4,
      baselines=baseline, target=0, return_convergence_delta=True)
print('IG + SmoothGrad 归因:', attributions)
print('收敛误差:', delta)

输出

IG + SmoothGrad 归因: tensor([[-0.4574, -1.5493, -1.0893],
                                      [ 0.0000, -0.2647, -5.1619]])
收敛误差: tensor([ 0.0000e+00,  2.3842e-07,  0.0000e+00, -2.3842e-07,  0.0000e+00,
        -4.7684e-07,  0.0000e+00, -4.7684e-07])

delta 张量中的元素数量等于：nt_samples * input.shape[0] 为了获得每个示例的增量，我们可以例如对它们取平均值：

deltas_per_example = torch.mean(delta.reshape(input.shape[0], -1), dim=1)

让我们深入了解我们网络的内部，理解哪些层和神经元对预测很重要。

我们将从 NeuronConductance 开始。NeuronConductance 帮助我们识别对给定层中特定神经元 重要的输入特征。它通过链式法则分解积分梯度的计算，将神经元的重要性定义为输出相对于 神经元的导数与神经元相对于模型输入的导数的路径积分。

在这种情况下，我们选择分析线性层中的第一个神经元。

nc = NeuronConductance(model, model.lin1)
attributions = nc.attribute(input, neuron_selector=1, target=0)
print('神经元归因:', attributions)

输出

神经元归因: tensor([[ 0.0000,  0.0000,  0.0000],
                             [ 1.3358,  0.0000, -1.6811]])

层导电性显示了神经元对给定输入的层的重要性。 它是隐藏层路径积分梯度的扩展，同样具有完整性属性。

它不将贡献分数归因于输入特征，而是显示所选层中每个神经元的重要性。

lc = LayerConductance(model, model.lin1)
attributions, delta = lc.attribute(input, baselines=baseline, target=0, return_convergence_delta=True)
print('层归因:', attributions)
print('收敛误差:', delta)

输出

层归因: tensor([[ 0.0000,  0.0000, -3.0856],
                            [ 0.0000, -0.3488, -4.9638]], grad_fn=<SumBackward1>)
收敛误差: tensor([0.0630, 0.1084])

与其他返回收敛误差的归因算法类似，LayerConductance 返回每个示例的误差。 近似误差是收敛误差的绝对值，可以作为给定输入和基线的积分近似准确度的代理。

有关支持的算法列表以及如何在不同类型的模型上应用 Captum 的更多详细信息， 可以在我们的教程中找到。

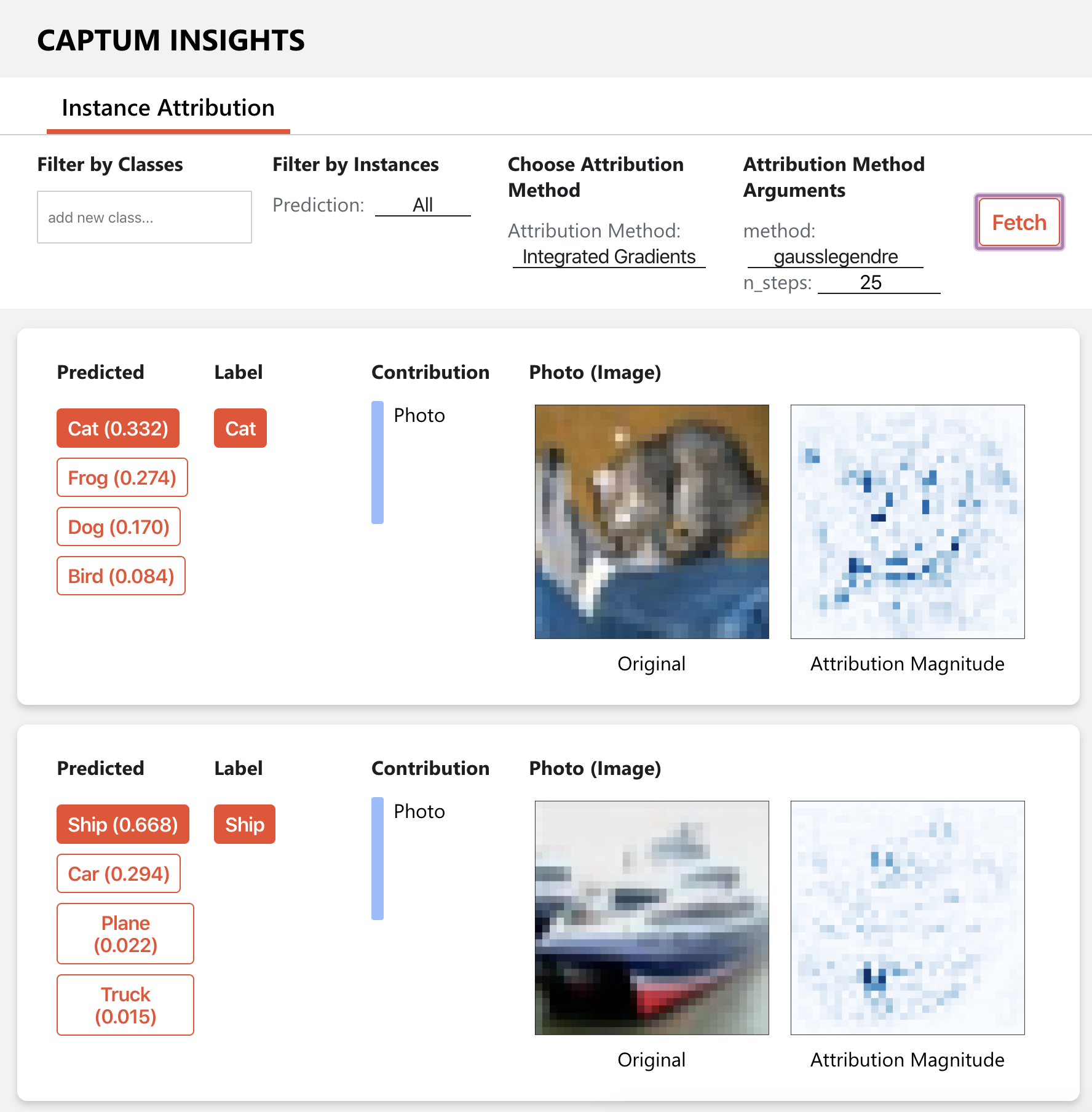
Captum Insights

Captum 提供了一个名为 Insights 的 Web 界面，可以轻松可视化并访问多种可解释性算法。

要通过 Captum Insights 分析 CIFAR10 上的示例模型，请运行

python -m captum.insights.example

然后在浏览器中打开输出中指定的 URL。

要构建 Insights，你需要 Node >= 8.x 和 Yarn >= 1.5。

要在 conda 环境中从检出构建并启动，请运行

conda install -c conda-forge yarn
BUILD_INSIGHTS=1 python setup.py develop
python captum/insights/example.py

Captum Insights Jupyter 小部件

Captum Insights 还有一个 Jupyter 小部件，提供与网页应用相同的用户界面。 要安装并启用该小部件，请运行

jupyter nbextension install --py --symlink --sys-prefix captum.insights.attr_vis.widget
jupyter nbextension enable captum.insights.attr_vis.widget --py --sys-prefix

要在 conda 环境中从检出构建小部件，请运行

conda install -c conda-forge yarn
BUILD_INSIGHTS=1 python setup.py develop

常见问题

如果您对使用 Captum 方法有疑问，请查看此常见问题解答，其中解答了许多常见问题。

贡献

有关如何提供帮助，请参阅贡献指南文件。

演讲和论文

NeurIPS 2019: 我们演讲的幻灯片可以在这里找到

KDD 2020: 我们在 KDD 2020 教程中的演讲幻灯片可以在这里找到。 您可以在这里观看录制的演讲

GTC 2020: 打开黑匣子：使用 Captum 和 PyTorch 进行模型理解。 您可以在这里观看录制的演讲

XAI 峰会 2020: 使用 Captum 和 Fiddler 通过可解释 AI 改进模型理解。 您可以在这里观看录制的演讲

PyTorch 开发者日 2020 模型可解释性。 您可以在这里观看录制的演讲

NAACL 2021 深度 NLP 模型中细粒度解释和因果分析教程。 您可以在这里观看录制的演讲

ICLR 2021 负责任 AI 研讨会:

• 关于 Captum 库的论文
• 关于调查显著性图完整性检查的论文

里昂大学医学影像暑期学校。模型可解释性课程（视频链接） https://www.youtube.com/watch?v=vn-jLzY67V0

算法参考

• IntegratedGradients、LayerIntegratedGradients：深度网络的公理化归因，Mukund Sundararajan等，2017和模型理解了问题吗？Pramod K. Mudrakarta等，2018
• InputXGradient：不只是黑盒：通过传播激活差异学习重要特征，Avanti Shrikumar等，2016
• SmoothGrad：SmoothGrad：通过添加噪声来去除噪声，Daniel Smilkov等，2017
• NoiseTunnel：显著性图的合理性检查，Julius Adebayo等，2018
• NeuronConductance：一个神经元有多重要？Kedar Dhamdhere等，2018
• LayerConductance：计算效率高的内部神经元重要性度量，Avanti Shrikumar等，2018
• DeepLift、NeuronDeepLift、LayerDeepLift：通过传播激活差异学习重要特征，Avanti Shrikumar等，2017和深度神经网络基于梯度的归因方法的更好理解，Marco Ancona等，2018
• NeuronIntegratedGradients：计算效率高的内部神经元重要性度量，Avanti Shrikumar等，2018
• GradientShap、NeuronGradientShap、LayerGradientShap、DeepLiftShap、NeuronDeepLiftShap、LayerDeepLiftShap：解释模型预测的统一方法，Scott M. Lundberg等，2017
• InternalInfluence：深度卷积网络的影响导向解释，Klas Leino等，2018
• Saliency、NeuronGradient：深入卷积网络内部：可视化图像分类模型和显著性图，K. Simonyan等，2014
• GradCAM、Guided GradCAM：Grad-CAM：通过基于梯度的定位实现深度网络的视觉解释，Ramprasaath R. Selvaraju等，2017
• Deconvolution、Neuron Deconvolution：可视化和理解卷积网络，Matthew D Zeiler等，2014
• Guided Backpropagation、Neuron Guided Backpropagation：追求简单性：全卷积网络，Jost Tobias Springenberg等，2015
• Feature Permutation：排列特征重要性
• Occlusion：可视化和理解卷积网络
• Shapley Value：n人博弈的值。博弈理论贡献 2.28 (1953): 307-317
• Shapley Value Sampling：基于采样的Shapley值多项式计算
• Infidelity and Sensitivity：关于解释的（不）忠实度和敏感性
• TracInCP, TracInCPFast, TracInCPRandProj：通过追踪梯度下降估计训练数据影响
• SimilarityInfluence：[基于预定义相似性度量的训练和测试样本间的成对相似性]
• BinaryConcreteStochasticGates：具有二元具体分布的随机门
• GaussianStochasticGates：具有高斯分布的随机门

关于上述归因算法的更多详细信息及其优缺点可以在我们的网站上找到。

许可证

Captum采用BSD许可证，详见LICENSE文件。