PyTorch 可微分 ODE 求解器实现

本库提供了用 PyTorch 实现的常微分方程（ODE）求解器。使用伴随方法支持通过 ODE 解进行反向传播，具有恒定的内存开销。有关 ODE 求解器在深度学习应用中的使用，请参见参考文献 [1]。

由于求解器是用 PyTorch 实现的，本仓库中的算法可以完全支持在 GPU 上运行。

安装

安装最新稳定版：

pip install torchdiffeq

安装 GitHub 上的最新版：

pip install git+https://github.com/rtqichen/torchdiffeq

示例

示例位于 examples 目录中。

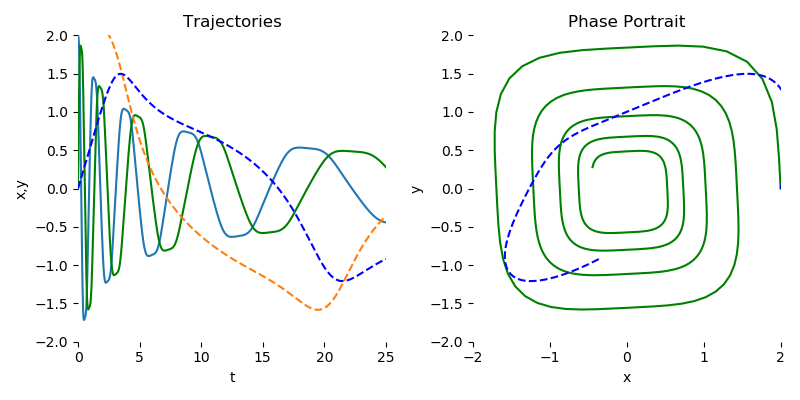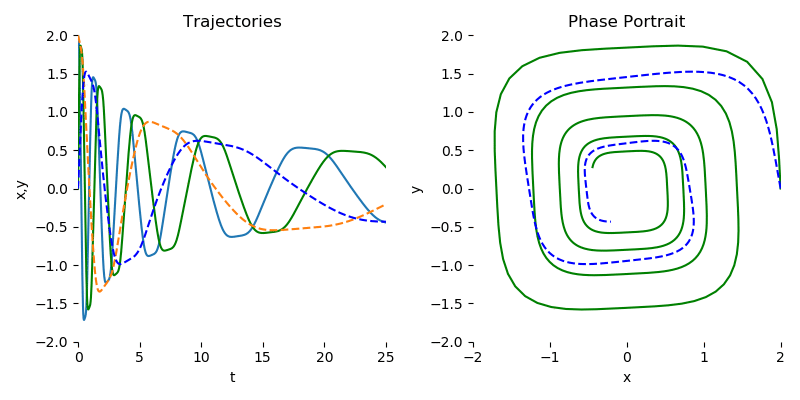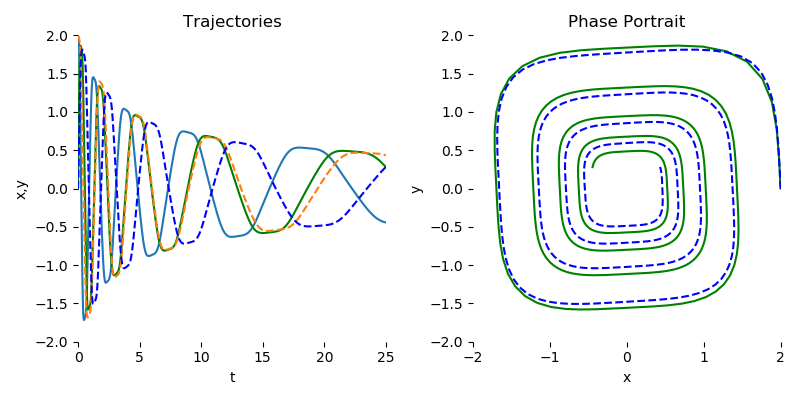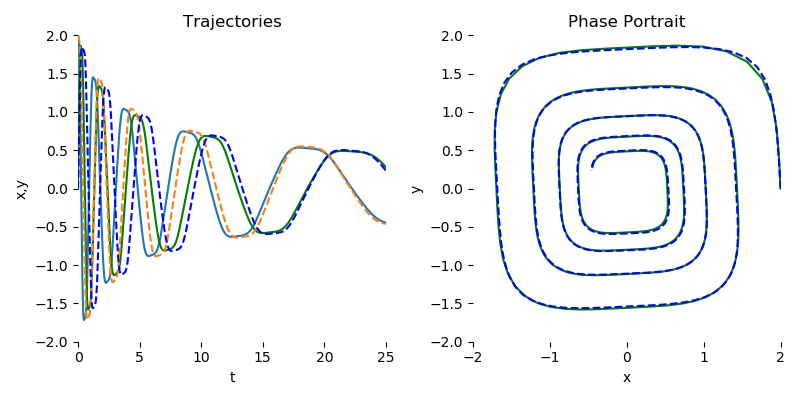
我们鼓励有兴趣使用本库的人查看 examples/ode_demo.py，以了解如何使用 torchdiffeq 拟合简单的螺旋 ODE。

ODE 演示

基本用法

本库提供了一个主要接口 odeint，其中包含用于解决初值问题（IVP）的通用算法，并为所有主要参数实现了梯度。初值问题由一个 ODE 和一个初值组成，

dy/dt = f(t, y)    y(t_0) = y_0.

ODE 求解器的目标是找到一条满足 ODE 并通过初始条件的连续轨迹。

使用默认求解器解决 IVP：

from torchdiffeq import odeint

odeint(func, y0, t)

其中 func 是实现常微分方程 f(t, x) 的任何可调用对象，y0 是表示初始值的任意维度张量，t 是包含评估点的一维张量。初始时间取为 t[0]。

通过 odeint 进行反向传播会经过求解器的内部过程。请注意，对于所有求解器来说，这在数值上并不稳定（但使用默认的 dopri5 方法可能没问题）。相反，我们鼓励使用 [1] 中解释的伴随方法，该方法由于 O(1) 的内存使用，可以根据需要进行任意多的步骤求解。

使用伴随方法：

from torchdiffeq import odeint_adjoint as odeint

odeint(func, y0, t)

odeint_adjoint 只是对 odeint 进行了简单的封装，但在反向调用中会求解一个伴随 ODE，以换取 O(1) 的内存使用。

最大的注意事项是，使用伴随方法时，func 必须是一个 nn.Module。这用于收集微分方程的参数。

可微分事件处理

我们允许基于事件函数终止 ODE 解。支持通过大多数求解器进行反向传播。有关事件处理在深度学习应用中的使用，请参见参考文献 [2]。

可以使用 odeint_event 调用：

from torchdiffeq import odeint_event
odeint_event(func, y0, t0, *, event_fn, reverse_time=False, odeint_interface=odeint, **kwargs)

func 和 y0 与 odeint 相同。
t0 是表示初始时间值的标量。
event_fn(t, y) 返回一个张量，是必需的关键字参数。
reverse_time 是一个布尔值，指定是否应该反向求解。默认为 False。
odeint_interface 是 odeint 或 odeint_adjoint 之一，指定是否应使用伴随模式来微分 ODE 解。默认为 odeint。
**kwargs：任何剩余的关键字参数都会传递给 odeint_interface。

当 event_fn(t, y) 的一个元素等于零时，求解在事件时间 t 和状态 y 处终止。event_fn 的多个输出可用于指定多个事件函数，其中第一个触发的事件将终止求解。

odeint_event 返回事件时间和最终状态，这两者都可以微分。梯度将通过事件函数反向传播。注意：事件函数的参数必须在状态本身中才能获得梯度。

事件时间的数值精度由 atol 参数决定。

有关模拟和微分弹跳球的示例，请参见 examples/bouncing_ball.py。有关学习简单事件函数的示例代码，请参见 examples/learn_physics.py。

弹跳球

odeint(_adjoint) 的关键字参数

关键字参数：

rtol 相对容差。
atol 绝对容差。
method 下面列出的求解器之一。
options 求解器特定选项的字典，详见进一步文档。

ODE 求解器列表：

自适应步长：

dopri8 Dormand-Prince-Shampine 8 阶 Runge-Kutta 法。
dopri5 Dormand-Prince-Shampine 5 阶 Runge-Kutta 法 [默认]。
bosh3 Bogacki-Shampine 3 阶 Runge-Kutta 法。
fehlberg2 2 阶 Runge-Kutta-Fehlberg 法。
adaptive_heun 2 阶 Runge-Kutta 法。

固定步长：

euler 欧拉方法。
midpoint 中点法。
rk4 四阶 Runge-Kutta 法（3/8 规则）。
explicit_adams 显式 Adams-Bashforth 法。
implicit_adams 隐式 Adams-Bashforth-Moulton 法。

此外，SciPy 提供的所有求解器都可通过 scipy_solver 使用。

对于大多数问题，好的选择是默认的 dopri5，或者使用 rk4 并适当设置小的 options=dict(step_size=...)。调整容差（自适应求解器）或步长（固定求解器）可以在速度和精度之间进行权衡。

常见问题

查看我们的 FAQ 了解常见问题。

进一步文档

有关伴随特定和求解器特定选项的详细信息，请查看进一步文档。

参考文献

可微分 ODE 求解器和事件处理的应用在以下两篇论文中讨论：

Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud. "Neural Ordinary Differential Equations." Advances in Neural Information Processing Systems. 2018. [arxiv]

@article{chen2018neuralode,
  title={Neural Ordinary Differential Equations},
  author={Chen, Ricky T. Q. and Rubanova, Yulia and Bettencourt, Jesse and Duvenaud, David},
  journal={Advances in Neural Information Processing Systems},
  year={2018}
}

Ricky T. Q. Chen, Brandon Amos, Maximilian Nickel. "Learning Neural Event Functions for Ordinary Differential Equations." International Conference on Learning Representations. 2021. [arxiv]

@article{chen2021eventfn,
  title={Learning Neural Event Functions for Ordinary Differential Equations},
  author={Chen, Ricky T. Q. and Amos, Brandon and Nickel, Maximilian},
  journal={International Conference on Learning Representations},
  year={2021}
}

计算伴随的半范数选项在以下论文中讨论：

Patrick Kidger, Ricky T. Q. Chen, Terry Lyons. "'Hey, that's not an ODE': Faster ODE Adjoints via Seminorms." International Conference on Machine Learning. 2021. [arxiv]

@article{kidger2021hey,
  title={"Hey, that's not an ODE": Faster ODE Adjoints via Seminorms.},
  author={Kidger, Patrick and Chen, Ricky T. Q. and Lyons, Terry J.},
  journal={International Conference on Machine Learning},
  year={2021}
}

如果您在研究中发现本库有用，请考虑引用。

@misc{torchdiffeq,
	author={Chen, Ricky T. Q.},
	title={torchdiffeq},
	year={2018},
	url={https://github.com/rtqichen/torchdiffeq},
}