ccma

alt text

❞纯粹由数据驱动的方法的魅力。❞—ChatGPT

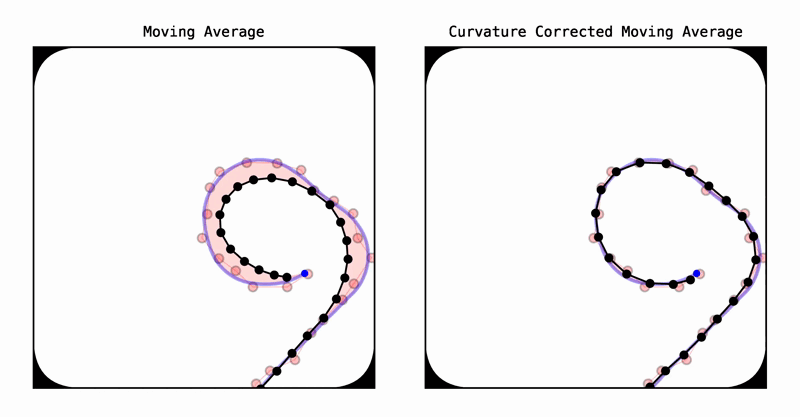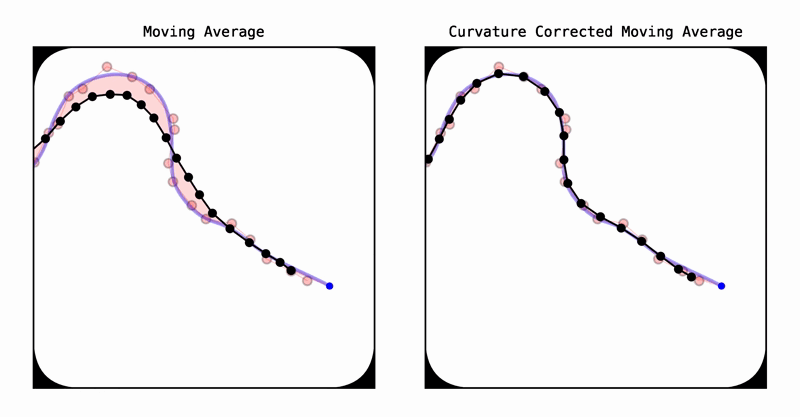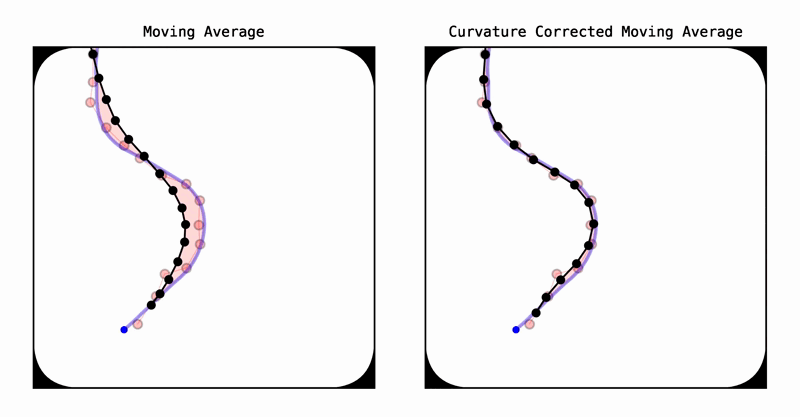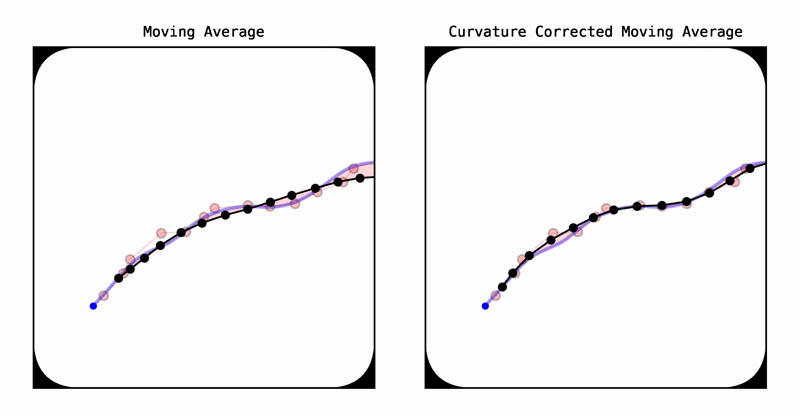
alt text

曲率校正移动平均（CCMA）是一种无模型、通用的2D/3D路径平滑算法。它解决了传统移动平均滤波器在曲线处常见的向内弯曲现象。CCMA方法采用对称滤波。然而，由于其对称性，它主要用于精确平滑而非状态估计。

该实现提供了用户友好的体验（参见最小工作示例），使得对以numpy数组表示的给定点进行滤波变得非常简单。用户可以轻松选择不同的核函数，包括截断正态分布、汉宁窗、均匀分布或复杂的帕斯卡三角核（默认）。

此外，该实现提供了不同的边界处理方式—填充、环绕、减小滤波宽度，或者完全不使用边界策略。这种适应性确保了实现可以满足广泛的场景和偏好。

虽然代码本身可能无法提供完整的理解，但可以在这篇信息丰富的文章或原始论文中找到更多细节和见解。

如果您使用CCMA，请考虑引用原始论文：

@inproceedings{Steinecker23,
  title={A Simple and Model-Free Path Filtering Algorithm for Smoothing and Accuracy},
  author={Steinecker, Thomas and Wuensche, Hans-Joachim},
  booktitle={2023 IEEE Intelligent Vehicles Symposium (IV)},
  pages={1--7},
  year={2023},
  organization={IEEE}
}

最小工作示例

import numpy as np
from ccma import CCMA

# 在单位圆上创建带噪声的点
n = 50
noise = np.random.normal(0, 0.05, (n, 2))
points = np.array([np.cos(np.linspace(0, 2*np.pi, n)),
                   np.sin(np.linspace(0, 2*np.pi, n))]).T
noisy_points = points + noise

# 创建ccma对象并使用填充（默认）和帕斯卡三角核/权重（默认）平滑点
ccma = CCMA(w_ma=5, w_cc=3)
smoothed_points = ccma.filter(noisy_points)

安装

要轻松安装CCMA，请使用以下pip命令：

pip3 install git+https://github.com/UniBwTAS/ccma.git#egg=ccma

或

python3 -m pip install git+https://github.com/UniBwTAS/ccma.git#egg=ccma

成功安装后，请按照以下步骤确保设置正确：

打开新的终端窗口。
启动Python shell：
```
python
```
通过导入CCMA模块验证安装：
```
>>> import ccma
```
确认版本号以确保安装成功：
```
>>> ccma.__version__
"1.0.0"
```

使用指南

更多信息可以在使用指南中找到。

CCMA用于路径插值

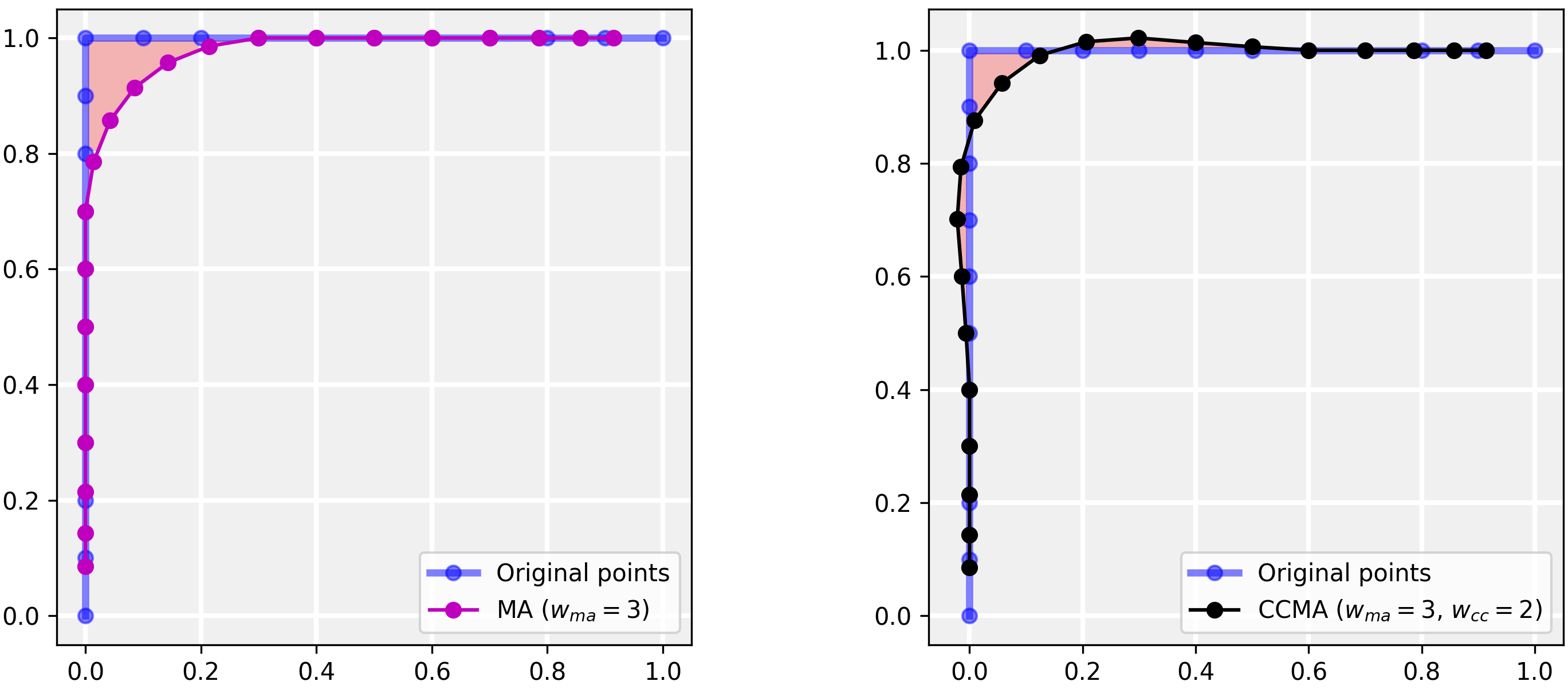
CCMA最初设计用于平滑嘈杂的路径；然而，由于其优越的特性和简单的使用方法，我们相信它可以服务于更多应用，如路径插值。在下图中，可以看出CCMA与MA相比，不仅减少了总体误差，还降低了最大误差。在提供的示例列表中，您可以找到路径插值的示例实现。

alt text

样条曲线vs. CCMA

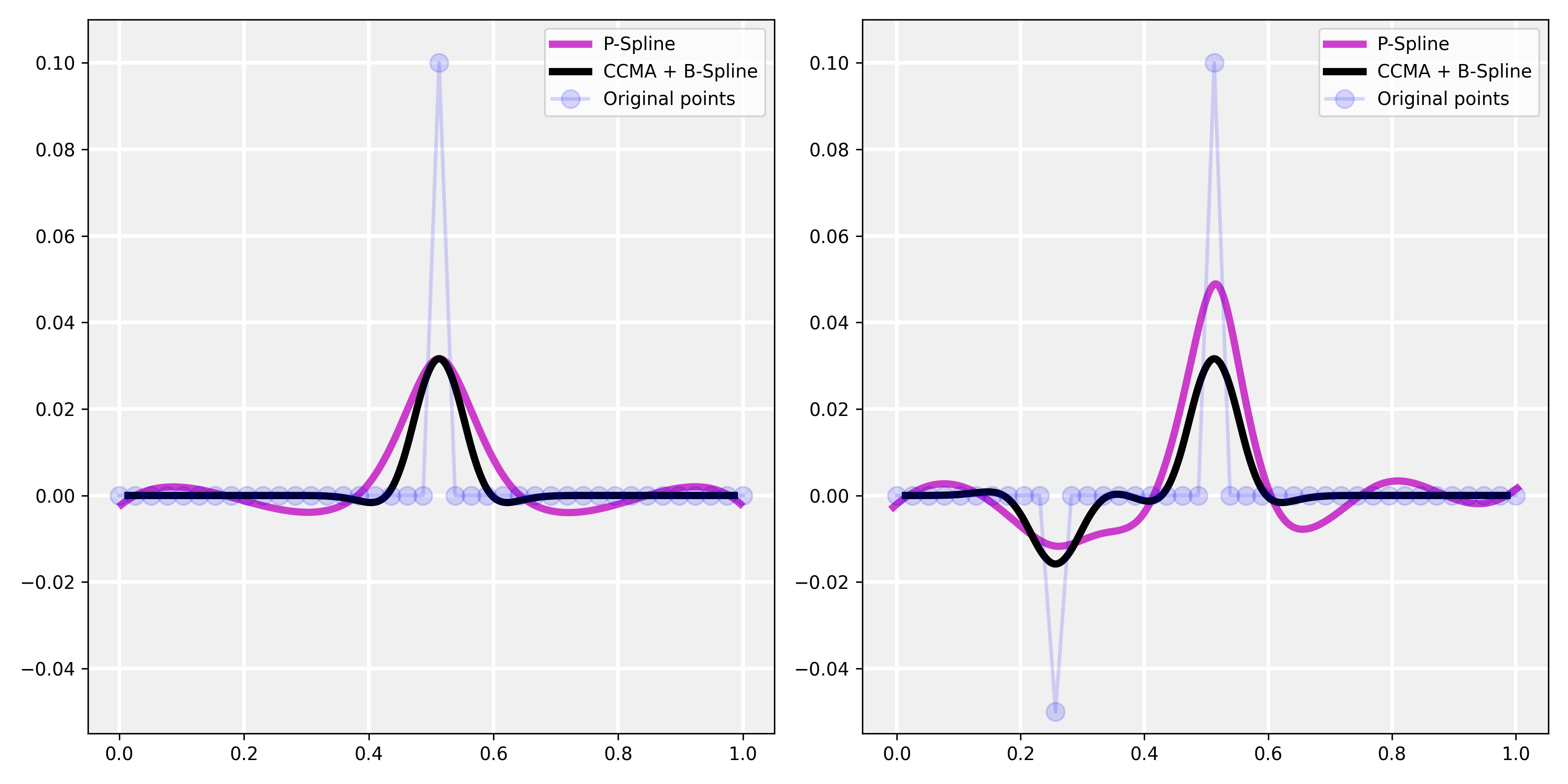
样条曲线通常被选用于插值和平滑；然而，局部变化可能会产生全局影响，导致意外或不期望的行为。相比之下，CCMA专门设计为仅受局部变化影响，使其成为一个稳健且可预测的选项。下图说明了这一区别。在左侧，可以看到CCMA仅在异常值附近受到影响，而P样条在整个长度上发生振荡。在右侧图中，引入了另一个异常值，再次仅局部影响CCMA。相反，P样条经历了显著的全局形状变化，之前的峰值增加，后续振荡变得更加明显。

另一个值得注意的方面是可以将CCMA与B样条结合使用。这会得到一个连续函数，但输出比P样条更可预测和直观。在下图中，首先应用了CCMA，然后将结果用于B样条生成。在示例列表中也可以找到一个说明性示例。

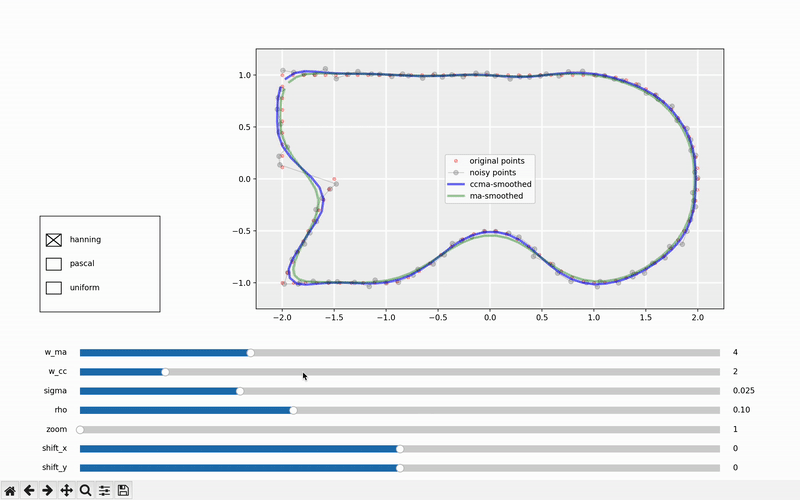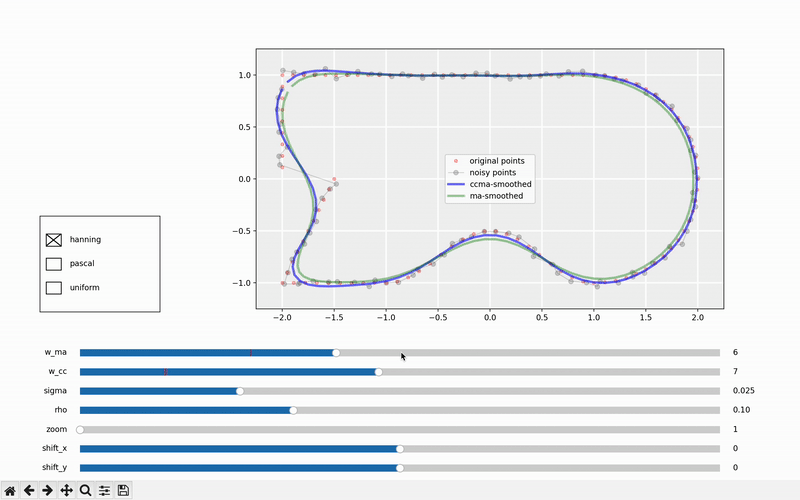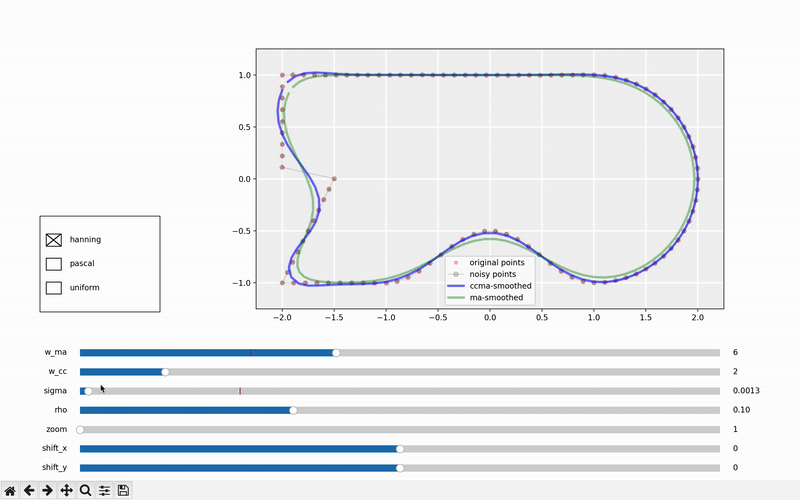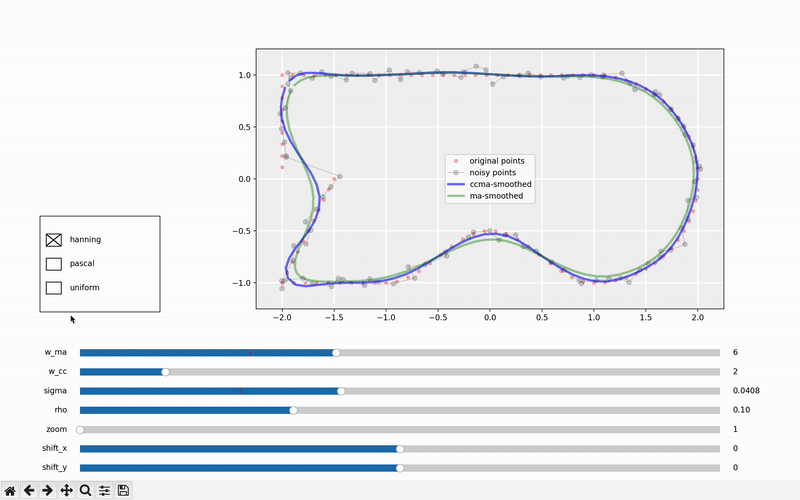
alt text