<SOURCE_TEXT>

PyTorch可微分SDE求解器的实现

此库提供了具有GPU支持和高效反向传播的随机微分方程（SDE）求解器。

安装

pip install torchsde

**要求：**Python >=3.8 和 PyTorch >=1.6.0。

文档

点击这里查看。

示例

快速示例

import torch  
import torchsde

batch_size, state_size, brownian_size = 32, 3, 2  
t_size = 20

class SDE(torch.nn.Module):  
    noise_type = 'general'  
    sde_type = 'ito'  

    def __init__(self):  
        super().__init__()  
        self.mu = torch.nn.Linear(state_size, state_size)  
        self.sigma = torch.nn.Linear(state_size, state_size * brownian_size)  

    # 漂移项  
    def f(self, t, y):  
        return self.mu(y)  # 形状为(batch_size, state_size)  

    # 扩散项  
    def g(self, t, y):  
        return self.sigma(y).view(batch_size, state_size, brownian_size)  

sde = SDE()  
y0 = torch.full((batch_size, state_size), 0.1)  
ts = torch.linspace(0, 1, t_size)  
# 初始状态y0，SDE将在区间[ts[0], ts[-1]]上被求解。  
# ys的形状将为(t_size, batch_size, state_size)  
ys = torchsde.sdeint(sde, y0, ts)

Notebook

examples/demo.ipynb提供了如何求解SDE的简短指南，包括修复求解器中随机性以及选择噪声类型等细微之处。

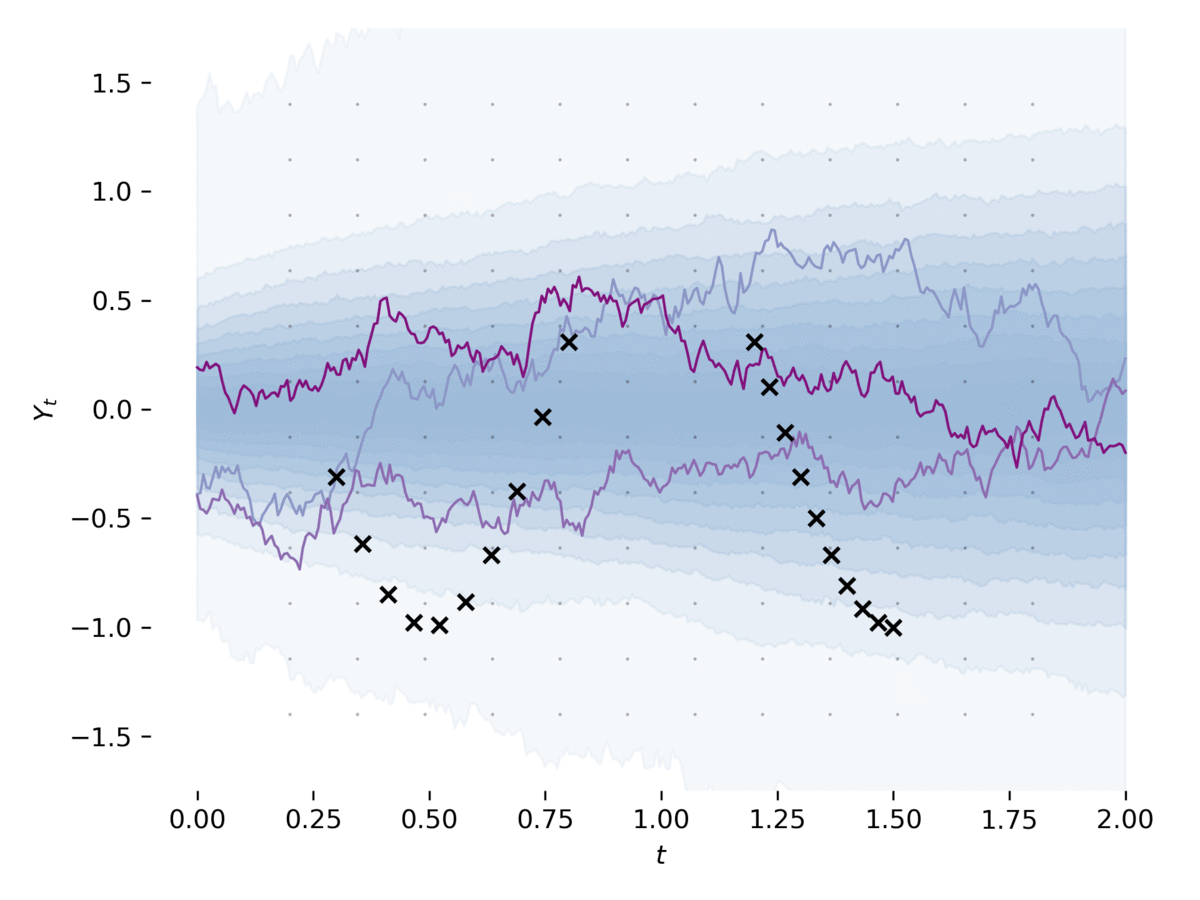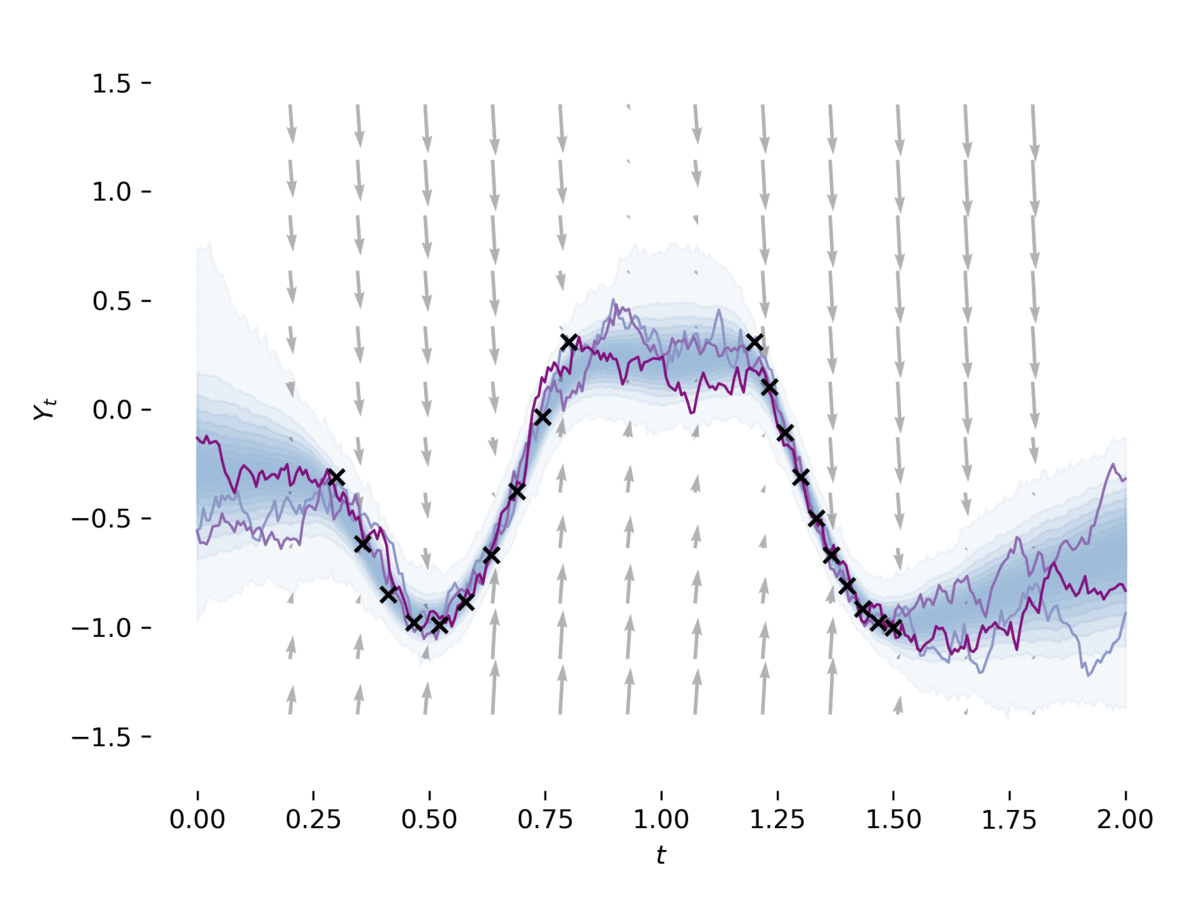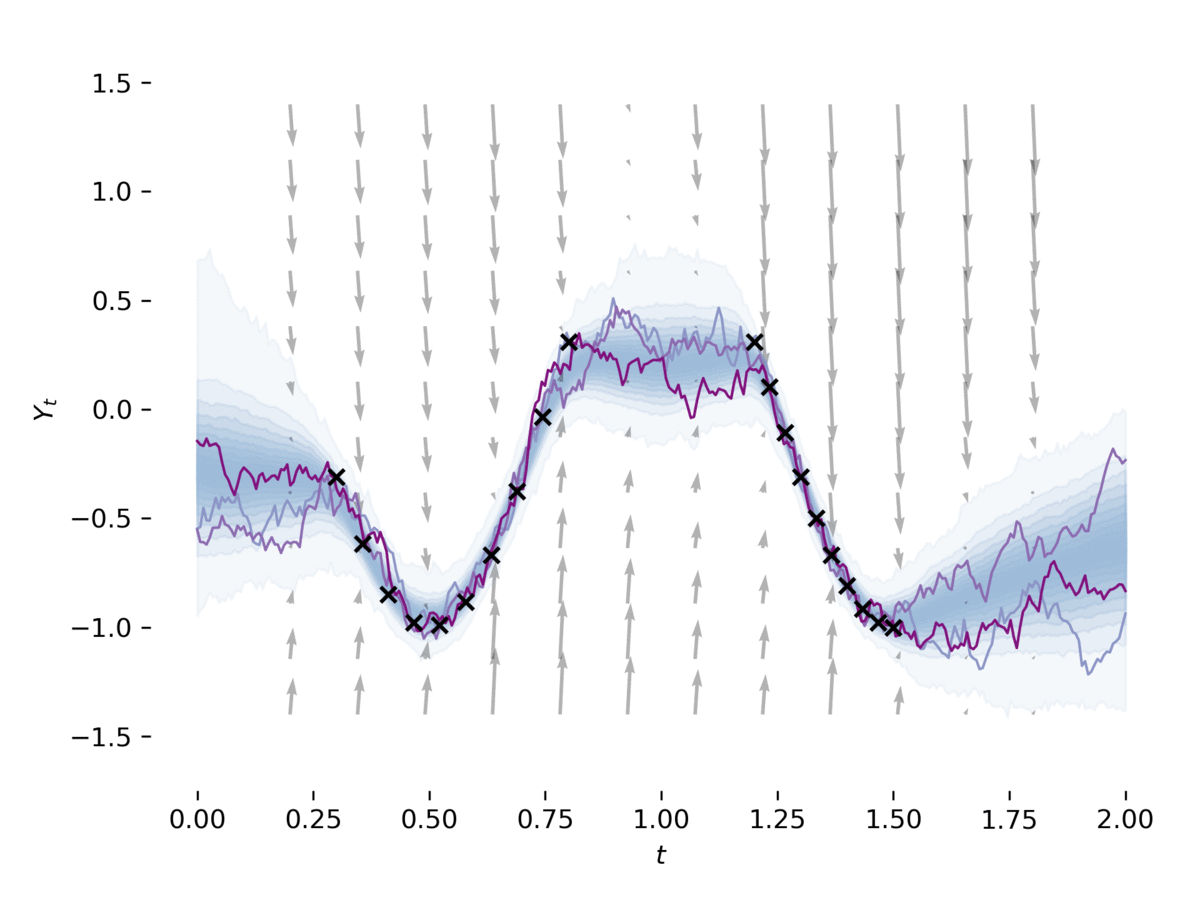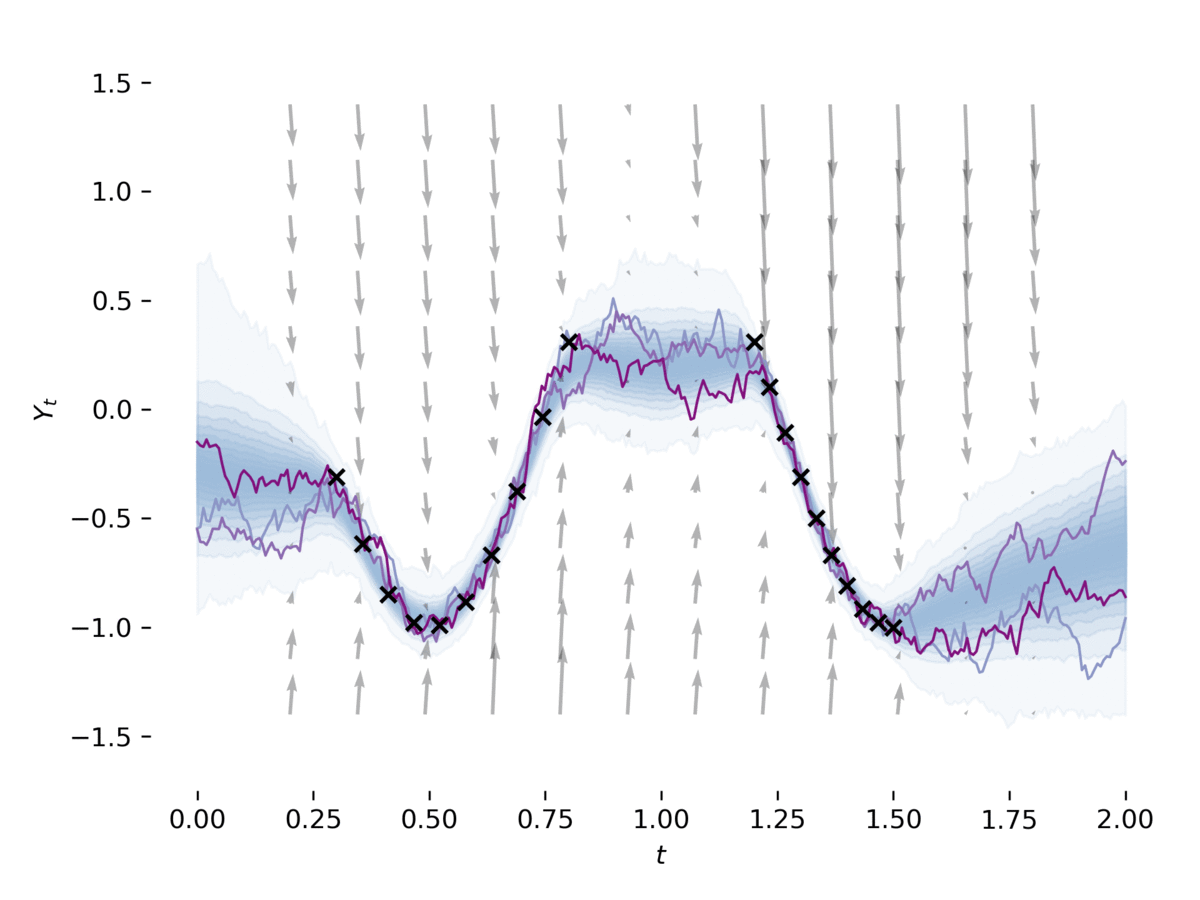
Latent SDE

examples/latent_sde.py学习潜在随机微分方程，如[1]的第5节所述。
该示例将SDE拟合到数据中，同时将其正则化为类似Ornstein-Uhlenbeck的先验过程。
该模型可以大致看作是一种变分自编码器，其先验和近似后验均为SDE。此示例可以通过以下命令运行

python -m examples.latent_sde --train-dir <TRAIN_DIR>

程序会将输出的图像保存到<TRAIN_DIR>指定的路径中。
在默认超参数下，训练应在500次迭代后趋于稳定。

Neural SDEs as GANs

examples/sde_gan.py学习作为GAN的SDE，如[2]、[3]中所述。
该示例将SDE作为GAN的生成器进行训练，同时使用神经CDE [4]作为判别器。此示例可以通过以下命令运行

python -m examples.sde_gan

引用

如果您在研究中发现此代码库有用，请考虑引用以下任意或全部文献：

@article{li2020scalable,  
  title={Scalable gradients for stochastic differential equations},  
  author={Li, Xuechen and Wong, Ting-Kam Leonard and Chen, Ricky T. Q. and Duvenaud, David},  
  journal={International Conference on Artificial Intelligence and Statistics},  
  year={2020}  
}

@article{kidger2021neuralsde,  
  title={Neural {SDE}s as {I}nfinite-{D}imensional {GAN}s},  
  author={Kidger, Patrick and Foster, James and Li, Xuechen and Oberhauser, Harald and Lyons, Terry},  
  journal={International Conference on Machine Learning},  
  year={2021}  
}

参考文献

[1] Xuechen Li, Ting-Kam Leonard Wong, Ricky T. Q. Chen, David Duvenaud. "Scalable Gradients for Stochastic Differential Equations". 国际人工智能与统计会议 2020. [arXiv]

[2] Patrick Kidger, James Foster, Xuechen Li, Harald Oberhauser, Terry Lyons. "Neural SDEs as Infinite-Dimensional GANs". 国际机器学习会议 2021. [arXiv]

[3] Patrick Kidger, James Foster, Xuechen Li, Terry Lyons. "Efficient and Accurate Gradients for Neural SDEs". 2021. [arXiv]

[4] Patrick Kidger, James Morrill, James Foster, Terry Lyons, "Neural Controlled Differential Equations for Irregular Time Series". 神经信息处理系统会议 2020. [arXiv]

这是一个研究项目，而非官方Google产品。

</SOURCE_TEXT>