时间序列距离

这是DTAI研究组使用的时间序列距离（如动态时间规整）库。该库提供了纯Python实现和快速的C语言实现。C语言实现只依赖Cython。它与Numpy和Pandas兼容，并且实现时避免了不必要的数据复制操作。

文档：http://dtaidistance.readthedocs.io

示例：

from dtaidistance import dtw
import numpy as np
s1 = np.array([0.0, 0, 1, 2, 1, 0, 1, 0, 0])
s2 = np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0])
d = dtw.distance_fast(s1, s2)

引用本工作：

Wannes Meert, Kilian Hendrickx, Toon Van Craenendonck, Pieter Robberechts, Hendrik Blockeel & Jesse Davis.
DTAIDistance (版本 v2). Zenodo.
http://doi.org/10.5281/zenodo.5901139

v2新特性：

Numpy现在是可选依赖项，编译C库时也不再需要（只需要Cython）。
对C代码进行了小幅优化以提高速度。
一致使用ssize_t而非int，允许在64位机器上使用更大的数据结构，并与Numpy更兼容。
并行化现在直接在C中实现（如果安装了OpenMP则包含）。
max_dist参数与Silva和Batista的PrunedDTW工作[7]类似。该工具箱现在实现了一个等同于PrunedDTW的版本，因为它修剪了更多的部分距离。此外，添加了use_pruning参数，可以自动将max_dist设置为欧几里得距离，如Silva和Batista所建议的那样，以加速计算（新方法ub_euclidean可用）。
C库中支持dtaidistance.dtw_ndim包中的多维序列。
用于聚类的DTW重心平均（v2.2）。
子序列搜索和局部并发（v2.3）。
支持N维时间序列（v2.3.7）。

安装

$ pip install dtaidistance

或

$ conda install -c conda-forge dtaidistance

pip安装需要Numpy作为依赖项来编译与Numpy兼容的C代码（使用Cython）。但是，这个依赖项是可选的，可以移除。

源代码可在github.com/wannesm/dtaidistance获取。

如果在编译过程中遇到任何问题（例如，基于C的实现或OpenMP不可用），请参阅文档了解更多选项。

使用

动态时间规整（DTW）距离度量

from dtaidistance import dtw
from dtaidistance import dtw_visualisation as dtwvis
import numpy as np
s1 = np.array([0., 0, 1, 2, 1, 0, 1, 0, 0, 2, 1, 0, 0])
s2 = np.array([0., 1, 2, 3, 1, 0, 0, 0, 2, 1, 0, 0, 0])
path = dtw.warping_path(s1, s2)
dtwvis.plot_warping(s1, s2, path, filename="warp.png")

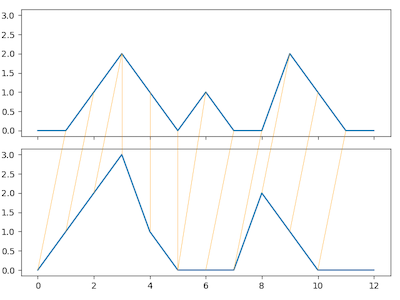
动态时间规整（DTW）示例

两个序列之间的DTW距离度量

仅基于两个数字序列的距离度量：

from dtaidistance import dtw
s1 = [0, 0, 1, 2, 1, 0, 1, 0, 0]
s2 = [0, 1, 2, 0, 0, 0, 0, 0, 0]
distance = dtw.distance(s1, s2)
print(distance)

最快的版本（快30-300倍）直接使用C，但需要数组作为输入（使用double类型），并且（可选）通过将max_dist设置为欧几里得上界来修剪计算：

from dtaidistance import dtw
import array
s1 = array.array('d',[0, 0, 1, 2, 1, 0, 1, 0, 0])
s2 = array.array('d',[0, 1, 2, 0, 0, 0, 0, 0, 0])
d = dtw.distance_fast(s1, s2, use_pruning=True)

或者你可以使用numpy数组（dtype为double或float）： from dtaidistance import dtw import numpy as np s1 = np.array([0, 0, 1, 2, 1, 0, 1, 0, 0], dtype=np.double) s2 = np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0]) d = dtw.distance_fast(s1, s2, use_pruning=True)

查看 __doc__ 以获取可用参数的信息：

print(dtw.distance.doc)

提供了一些选项来提前停止动态规划算法正在探索的一些路径或调整距离度量计算：

window：仅允许在两条对角线附近进行此数量的偏移。
max_dist：如果返回的距离度量大于此值，则停止。
max_step：不允许步长大于此值。
max_length_diff：如果两个序列的长度差大于此值，则返回无穷大。
penalty：如果应用压缩或扩展，则添加的惩罚（在距离之上）。
psi：Psi 松弛以忽略序列的开始和/或结束（用于循环序列）[2]。
use_pruning：基于欧几里得上界进行剪枝计算。

DTW 距离度量所有扭曲路径

如果除了距离外，还想要完整的矩阵来查看所有可能的扭曲路径：

from dtaidistance import dtw s1 = [0, 0, 1, 2, 1, 0, 1, 0, 0] s2 = [0, 1, 2, 0, 0, 0, 0, 0, 0] distance, paths = dtw.warping_paths(s1, s2) print(distance) print(paths)

可以按如下方式可视化所有扭曲路径的矩阵：

from dtaidistance import dtw from dtaidistance import dtw_visualisation as dtwvis import random import numpy as np x = np.arange(0, 20, .5) s1 = np.sin(x) s2 = np.sin(x - 1) random.seed(1) for idx in range(len(s2)): if random.random() < 0.05: s2[idx] += (random.random() - 0.5) / 2 d, paths = dtw.warping_paths(s1, s2, window=25, psi=2) best_path = dtw.best_path(paths) dtwvis.plot_warpingpaths(s1, s2, paths, best_path)

注意 psi 参数，它放松了开始和结束处的匹配。在这个例子中，即使正弦波略有偏移，也能得到完美匹配。

一组序列之间的 DTW 距离度量

要计算序列列表中所有序列之间的 DTW 距离度量，请使用 dtw.distance_matrix 方法。您可以设置变量以使用更多或更少的 C 代码（use_c 和 use_nogil）以及并行或串行执行（parallel）。

distance_matrix 方法需要一个列表的列表/数组：

from dtaidistance import dtw import numpy as np series = [ np.array([0, 0, 1, 2, 1, 0, 1, 0, 0], dtype=np.double), np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0]), np.array([0.0, 0, 1, 2, 1, 0, 0, 0])] ds = dtw.distance_matrix_fast(series)

或者一个矩阵（如果所有序列长度相同）：

from dtaidistance import dtw import numpy as np series = np.matrix([ [0.0, 0, 1, 2, 1, 0, 1, 0, 0], [0.0, 1, 2, 0, 0, 0, 0, 0, 0], [0.0, 0, 1, 2, 1, 0, 0, 0, 0]]) ds = dtw.distance_matrix_fast(series)

限定为块的一组序列之间的 DTW 距离度量

您可以指示计算只填充距离度量矩阵的一部分。例如，将计算分布在多个节点上，或仅比较源序列和目标序列。

from dtaidistance import dtw import numpy as np series = np.matrix([ [0., 0, 1, 2, 1, 0, 1, 0, 0], [0., 1, 2, 0, 0, 0, 0, 0, 0], [1., 2, 0, 0, 0, 0, 0, 1, 1], [0., 0, 1, 2, 1, 0, 1, 0, 0], [0., 1, 2, 0, 0, 0, 0, 0, 0], [1., 2, 0, 0, 0, 0, 0, 1, 1]]) ds = dtw.distance_matrix_fast(series, block=((1, 4), (3, 5)))

在这种情况下，输出将是：

0 1 2 3 4 5

[[ inf inf inf inf inf inf] # 0 [ inf inf inf 1.4142 0.0000 inf] # 1 [ inf inf inf 2.2360 1.7320 inf] # 2 [ inf inf inf inf 1.4142 inf] # 3 [ inf inf inf inf inf inf] # 4 [ inf inf inf inf inf inf]] # 5

聚类

距离矩阵可用于时间序列聚类。你可以使用现有方法如scipy.cluster.hierarchy.linkage，或者使用两种包含的聚类方法之一（后者是SciPy linkage方法的封装）。

from dtaidistance import clustering
# 自定义层次聚类
model1 = clustering.Hierarchical(dtw.distance_matrix_fast, {})
cluster_idx = model1.fit(series)
# 增强Hierarchical对象以跟踪完整树
model2 = clustering.HierarchicalTree(model1)
cluster_idx = model2.fit(series)
# SciPy linkage聚类
model3 = clustering.LinkageTree(dtw.distance_matrix_fast, {})
cluster_idx = model3.fit(series)

对于跟踪完整聚类树的模型（HierarchicalTree或LinkageTree），可以将树可视化：

model.plot("myplot.png")

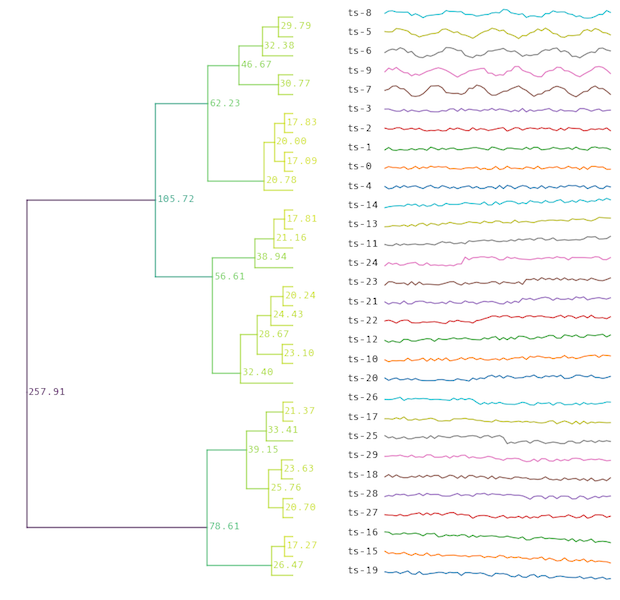
动态时间规整（DTW）层次聚类

依赖

Python 3

可选：

开发：

联系

https://people.cs.kuleuven.be/wannes.meert

参考文献

T. K. Vintsyuk, 基于动态规划的语音识别。 Kibernetika, 4:81–88, 1968.
H. Sakoe and S. Chiba, 用于口语识别的动态规划算法优化。 IEEE声学、语音和信号处理汇刊, 26(1):43–49, 1978.
C. S. Myers and L. R. Rabiner, 几种动态时间规整算法在连续词识别中的比较研究。贝尔系统技术期刊, 60(7):1389–1409, 1981年9月.
Mueen, A and Keogh, E, 从动态时间规整中提取最优性能, 教程, KDD 2016
D. F. Silva, G. E. A. P. A. Batista, and E. Keogh. 端点对动态时间规整的影响, SIGKDD时间序列挖掘与学习研讨会, II. 计算机协会-ACM, 2016.
C. Yanping, K. Eamonn, H. Bing, B. Nurjahan, B. Anthony, M. Abdullah and B. Gustavo. [UCR时间序列分类档案](https://github.com/wannesm/dtaidistance/blob/master/www.cs.ucr.edu/~eamonn/time_series_data/, 2015.
D. F. Silva and G. E. Batista. 加速全对动态时间规整矩阵计算, 2016年SIAM国际数据挖掘会议论文集, 837–845页. SIAM, 2016.

许可证

DTAI距离代码。

版权所有 2016-2022 KU Leuven, DTAI研究组

根据Apache许可证2.0版（"许可证"）授权；
除非遵守许可证，否则您不得使用此文件。
您可以在以下位置获取许可证副本：

    http://www.apache.org/licenses/LICENSE-2.0

除非适用法律要求或书面同意，否则根据许可证分发的软件是基于
"按原样"分发的，不附带任何明示或暗示的担保或条件。
有关许可证下的特定语言管理权限和限制，请参阅许可证。